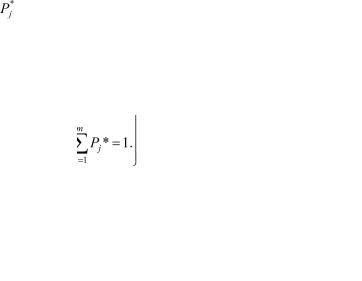baldin_kv_red_matematika_dlia_gumanitariev

12.МетОдыстатистическОйОбрабОтки реЗультатОвисПытаний

12.1.Постановказадачиоцениваниявероятностных характеристикслучайныхвеличин

Предположим, цель эксперимента состоит в определении вероятностных характеристик некоторой случайной величины X. При n независимых наблюдениях этой случайной величины получена случайная выборка {X1, X2, …, Xn}. Требуется по результатам ограниченного числа наблюдений {x1, x2, …, xn} выработать суждение о вероятностных характеристиках этой случайной величины.

Известно, что исчерпывающей вероятностной характеристикой случайной величины является закон ее распределения. Поэтому одной из задач обработки результатов испытаний является построение закона распределения случайной величины (статистической функции или статистической плотности распределения) по экспериментальным данным.

Часто для описания случайной величины достаточно знания ее числовых характеристик (математического ожидания, дисперсии, стандартного отклонения, других моментов). В этом случае возникает необходимость в определении по результатам испытаний значений этих характеристик.

Поскольку объем выборки ограничен, то методы математической статистики позволяют находить лишь приближенные значения указанных характеристик, т. е. их оценки.

При оценивании параметров в математической статистике используют два подхода: точечное и интервальное оценивание. При точечном оценивании по результатам испытаний находят число (точку на числовой оси), которое принимают в качестве приближенного значения оцениваемого параметра. Полученное число называют оценкой параметра. В дальнейшем оценку параметра будем обозначать * и использовать символическую запись * → ( * является точечной оценкой параметра ). В частности, параметром может быть математическое ожида-

91

ние mx, дисперсия Dx, стандартное отклонение sx, вероятность P наступления случайного события и другие параметры случайной величины.

Оценка параметра является функцией результатов испытаний, т. е. статистикой:

Следовательно, оценка * является случайной величиной с присущим ей законом распределения и числовыми характе-

ристиками. Знание вероятностных характеристик позволяет выявить статистические свойства оценок, устанавливать их точность и на этой основе выбирать наилучшие оценки.

При интервальном оценивании определяют интервал, который с заданной вероятностью накрывает истинное значение оцениваемого параметра. Границы интервала являются функциями результатов испытаний. Поэтому в общем случае границы интервала, а следовательно, и сам интервал, будут случайными:

где s (X1, X2, …, Xn), s0(X1, X2, …, Xn) — статистики, отличные от статистики (12.1) и в каждом конкретном случае определяемые соответствующими соотношениями.

В математической статистике рассматриваемый интервал принято называть доверительным интервалом, а вероятность, с которой он накрывает истинное значение параметра, — дове-

рительной вероятностью.

Основное назначение доверительных оценок — характеризовать качество точечных оценок, определяемое их точностью и надежностью (достоверностью).

12.2.Основныетребованиякоценкам

Вид оценки каждой числовой характеристики выбирают один раз применительно к исследованию любой случайной величины. Эту выбранную оценку используют во всех случаях

92

нахождения неизвестных значений данной числовой характеристики. Поэтому оценки выбирают так, чтобы при их массовом применении обеспечивалась наибольшая точность определения числовых характеристик. Чтобы оценки имели такое свойство, к ним предъявляют соответствующие требования

[1, 10, 14, 15].

1. Оценка параметра x должна быть несмещенной, т. е. математическое ожидание оценки должно быть равно истинному значению искомого параметра:

(12. )

Достоинством несмещенной оценки является то, что получаемые с ее помощью значения искомого параметра группируются около действительного значения этого параметра и при массовом применении такой оценки в среднем будут равны этому значению. Применение несмещенных оценок обеспечивает отсутствие систематических ошибок определения неизвестных значений характеристик.

Если то оценку называют положительно

смещенной, если — отрицательно смещенной.

На практике иногда используют оценки, которые при малом объеме выборки n являются смещенными, но при увеличении n величина смещения стремится к нулю. Такие оценки называют асимптотически несмещенными. Оценка — асимп-

тотически несмещенная, если выполняется условие

2. Оценка должна иметь минимальную дисперсию. Для одного и того же параметра можно подобрать не одну, а несколько несмещенных оценок. На рис. 12.1 показаны плотности вероятности трех несмещенных оценок параметра x, полученные при одном и том же объеме выборки n.

Как следует из рисунка, оценки имеют разные дисперсии. Поэтому значения параметра x, полученные с помощью этих оценок, будут иметь различное рассеивание относительно истинного значения этого па-

9

*

x x

Рис. 12.1. Плотности распределений различных оценок

раметра. Очевидно, что наилучшей из оценок является оценка с наименьшей дисперсией.

Отсюда вытекает, что одновременно с требованием несмещенности оценка должна удовлетворять еще одному требованию. Необходимо, чтобы при данном числе испытаний оценка имела минимальную дисперсию. Не-

смещенная оценка, имеющая минимальную дисперсию, называется эффективной оценкой.

Минимальная дисперсия несмещенной оценки определяется выражением

где n— объем выборки из генеральной совокупности;

I( x; x) — количество информации о параметре x, содержащееся в одном наблюдении, так называемое информационное количество Фишера.

где f (x, x) — плотность распределения случайной величины X.

94

Выражение для минимальной дисперсии смещенной оценки записывается в виде [1 , 14, 15]:

В качестве показателя эффективности оценки параметра x используют меру эффективности e, равную отношению минимально возможной величины дисперсии оценки к дисперсии данной конкретной оценки (0 # e # 1):

Асимптотической эффективностью ea оценки = s(X1, X2, …, Xn), полученной по независимой выборке, называют предел

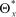если он существует. Оценка будет асимптотически эффективной, если ea() = 1.

. Оценка должна быть состоятельной, т. е. сходиться по вероятности с увеличением числа испытаний к оцениваемому параметру:

Состоятельная оценка должна быть асимптотически несмещенной, и с увеличением объема выборки дисперсия оценки должнауменьшаться.Поэтомувкачествесостоятельностиоценки можно принять одновременное выполнение двух равенств:

Таким образом, состоятельная оценка всегда асимптотически несмещенная и имеет минимальную дисперсию.

95

4.Желательно, чтобы оценка была прочной (робастной) или свободной (не зависящей от распределения).

Часто до проведения исследований закон распределения случайной величины X неизвестен. Поэтому не ясно, какую

оценку принять для параметра x. Целесообразно в этом случае воспользоваться оценкой, эффективность которой при некоторых распределениях может быть меньше единицы, но вид

еене меняется с изменением закона распределения.

5.Размерность оценки должна совпадать с размерностью оцениваемого параметра.

На практике получить оценку, удовлетворяющую всем перечисленным требованиям, удается не всегда. Поэтому необходимо анализировать те последствия, к которым приводят отступления от того или иного требования.

Оценки, удовлетворяющие указанным требованиям, могут быть получены различными методами. Поскольку в дальнейшем будут использоваться уже полученные оценки параметров, то здесь эти методы не рассматриваются. Они достаточно полно изложены в литературе по математической статистике.

12.3.Оцениваниезаконовраспределенияслучайныхвеличин

Как было отмечено в п. 11.1, одной из задач статистической обработки результатов испытаний является установление вида закона распределения случайной величины. На первом этапе решения этой задачи по результатам проведенных испытаний строят статистические функцию и плотность распределения. Анализ полученных графиков и природы исследуемой случайной величины обычно позволяет выдвинуть гипотезу о виде закона ее распределения. Затем по результатам испытаний проверяют справедливость выдвинутой гипотезы.

В данном пункте рассмотрим только первый этап решения указанной задачи.

Значения, принятые случайной величиной X при испытаниях, удобно представить в виде табл. 12.1, называемой прос-

той статистической совокупностью [5].

96

Таблица 12.1

Простая статистическая совокупность

Если результаты наблюдений разместить в порядке возрастания, то получаемая при этом таблица называется вариационным рядом (табл. 12.2). Элементы вариационно-

го ряда называются порядковыми (ранговыми) статис-

тиками. Номер элемента вариационного ряда называется

рангом.

В случае, когда исследуемая случайная величина дискретного типа или результаты измерений округляются, результаты нескольких наблюдений могут совпадать. Из этого следует, что различные результаты наблюдений могут появляться в выборке с различной частотой, определяемой по формуле

где nk — число появлений в выборке результата xk, . Вариационный ряд, представленный в форме табл. 12. ,

принято называть статистическим рядом.

По известному статистическому ряду строят статистическую (выборочную) функцию распределения F*(x) (рис. 12.2). Ординаты функции F*(x) обычно определяют в точках, отвечающих полученным значениям результатов измерений , по формуле в которой суммирование распространяется на значения , меньшие x.

97

Статистическая функция распределения является кусоч- но-непрерывной. Точками разрыва функции являются полученные значения xk, а величина разрыва в каждой точке численно равна частоте соответствующего результата в выборке. Если каждое из значений xk в выборке получено 1 раз, то величина разрыва в каждой точке одинакова и равна 1/n.

Основанием применимости статистической функции распределения F*(x) для оценивания истинной функции распределения F(x) служит закон больших чисел, в частности, предельная теорема В. И. Гливенко. В соответствии с этой теоремой можно утверждать, что при увеличении объема выборки F*(x) сходится по вероятности к F(x), т. е.

98

Таким образом, статистическая функция распределения F*(x) является состоятельной оценкой функции распределения F(x). Кроме того, она является несмещенной асимптотически эффективной оценкой [17]. Поэтому при достаточно большом n функцию распределения случайной величины можно приближенно заменять ее выборочной функцией распределения.

Однако при большом объеме выборки построение статистической функции распределения путем определения ее значений для каждого из полученных результатов FFF является трудоемким (статистический ряд становится громоздким). В этом случае результаты наблюдений подвергают предварительной обработке, суть которой заключается в следующем. Весь диапазон полученных результатов от xmin до xmax разбивают на m интервалов. Затем определяют частоту попадания результатов измерений в каждый интервал по формуле

где nj — число результатов измерений, попадающих в j-й интервал , включая его левую границу.

Число интервалов не должно быть слишком большим (в этом случае частоты подвергаются незакономерным колебаниям и статистический ряд становится невыразительным) или слишком малым (при этом описание случайной величины статистическим рядом становится грубым). Обычно выбирают 10–20 интервалов. Для ориентировочного определения числа интервалов можно пользоваться соотношениями m 5 lg(n) или [15]. При этом желательно, чтобы выполнялось условие nj $ 5.

Длины интервалов можно брать как одинаковыми, так и различными. Если имеет место значительная неравномерность распределения случайной величины, длины интервалов целесообразно брать различными.

В областях наибольшей изменчивости распределения интервалы должны быть более короткими. В случае, ког-

99

да интервалы различные, обработка экспериментальных данных несколько усложняется.

Итогом предварительной обработки результатов наблюдений является статистический ряд распределения случайной величины (табл. 12.4).

Статистическую функцию распределения строят в виде ломаной линии с вершинами в граничных точках выбранных интервалов (см. рис. 12. ). Ординаты функции F*(x) в этих точках равны накопленным частотам:

(12.4)

Знание статистического ряда позволяет построить статистическую плотность распределения f*(x), график которой принято называть гистограммой. Гистограмму строят следующим образом. На каждом из выбранных интервалов, как на основании, строят прямоугольники, площадь которых равна частоте попадания полученных результатов наблюдений на данный интервал. Высоты прямоугольников определяют из соотношения

400