(10. 9)
Проделав несложные преобразования в показателе степени, получим
(10.40)
Анализ формулы (10.40) показывает, что случайная величина Y распределена нормально с математическим ожиданием my = amx + b и стандартным отклонением sy = |a|sx. Здесь получено подтверждение общего правила: линейное преобразование случайной величины не изменяет вида закона ее распределения.
Распределениеполярныхкоординат
На практике часто осуществляется переход от прямоугольных к полярным координатам. Предположим, что известна плотность распределения прямоугольных координат f (x, y) и требуется определить плотность распределения системы полярных координат r, , если
X = Rcos ; Y = Rsin . |
(10.41) |
Как известно, якобиан преобразования (10.41) равен I = r. Тогда на основании общей формулы запишем
f (r, ) = rf (x, y) = rf (rcos , rsin ). |
(10.42) |
В частном случае, если {X, Y} — нормально распределенные величины с плотностью распределения
плотность распределения полярных координат имеет вид

(10.4 )
Рассмотрим теперь распределение случайной величины R при условии, что sx = sy = s, т. е. для нормального кругового распределения.
Применяя правило определения частного распределения при известной плотности совместного распределения, имеем
или
(10.44)
Получили плотность распределения Релея. Это распределение радиус-вектора, составляющие которого суть независимые нормально распределенные случайные величины с равными стандартными отклонениями.
10.5.распределениенеоднозначногопреобразования случайныхвеличин
Предположим, функция Y = c(X) такова, что обратная ей функция X = c(Y) неоднозначна, т. е. одному значению величины y соответствует несколько значений аргумента x (рис. 10. 2), которые обозначим x1 = c1(y); x2 = c2(y) и т. д. В данном случае функция будет немонотонная.
Событие y < Y < y + dy будет иметь место при наступлении хотя бы одного из нескольких несовместных событий:
x1 < X < x1 + dx1; x2 < X < x2 + dx2;… |
(10.45) |
Применяя теорему сложения вероятностей несовместных событий, получаем
P(y < Y < y + dy) = P(x1 < X < x1 + dx1) + + P(x2 < X < x2 + dx2) + …
|
|
|
y |
|
|
|
|
|
y |
|
|
x1 |
x2 |
x 0 |
x4 |
x5 |
x |
Рис. 10.2. График функции y = c(x) |
|
или
f (y)dy = f (x1)dx1 + f (x2)dx2 …
Из последнего равенства получаем искомую формулу для плотности распределения f (y) неоднозначного преобразования случайной величины:
(10.46)
Формулу (10.46) можно распространить и на многомерный случай [6, 1 ].
В качестве примера рассмотрим квадратичное преобразование случайной величины X:
Y = X2.
Каждому значению y, которое всегда положительно, отвечают два значения x:
Применяя формулу (10.46), получим
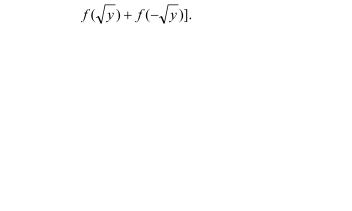
или
Пусть, например, случайная величина X распределена по нормальному закону с математическим ожиданием mx = 0 и стандартным отклонением sx. После квадратичного преобразования плотность распределения будет иметь вид:
Следовательно, результат квадратичного преобразования нормально распределенной случайной величины имеет распределение, отличное от нормального.
10.6.распределениефункциидвухслучайныхвеличин
Рассмотрим частный случай преобразования системы двух случайных величин, имеющий большое значение для практики, а именно функцию двух случайных аргументов
Z = w(X, Y).
Необходимо по известному распределению системы случайных величин {X, Y} определить распределение функции Z.
Чтобы воспользоваться полученным в п. 10.5 правилом для решения этой задачи, применим следующий прием. Введем в рассмотрение случайную величину Z1, равную X. Для общности рассуждений можно записать
При таком подходе систему случайных величин {Z1, Z2} можно рассматривать как результат функционального преобразования системы {X, Y}:
Z = w(X, Y); |
|
Z1 = w1(X, Y). |
(10.48) |
Предположим, что соответствующие обратные функции X = c1(Z1); Y = c2(Z, X) однозначны. К этому случаю применим полученное выше правило определения плотности распределения функционального однозначного преобразования.
Вычислим якобиан преобразования (10.48):
(10.49)
Применяя формулу (10. 5), получим
(10.50)
Теперь, используя правило определения частного распределения, найдем решение поставленной задачи:
или
(10.51)
так как dz1 = dx.
Из формулы (10.51) как частные случаи получаются формулы для определения плотности распределения суммы, разности, произведения и частного от деления двух случайных величин. Ограничимся рассмотрением наиболее важного для практики случая определения плотности распределения суммы двух случайных величин.
Предположим Z = X + Y. Тогда Z = X 2 Y,  и
и
(10.52)
Если случайные величины независимы, то
(10.5 )
Формула (10.5 ) носит наименование формулы композиции, или формулы свертки двух распределений. Эту формулу можно записать и в другом виде:
Аналогично могут быть получены формулы для определения плотности распределения разности, произведения и частного от деления двух случайных величин.
10.7.композицияраспределений
10.7.1.Композициянормальногоиравномерногораспределений
Композицией распределений называют распределение суммы независимых случайных величин [1, 7, 1 ]. В практике часто приходится рассматривать сумму двух случайных величин, одна из которых распределена по нормальному, а другая по равномерному закону.
Предположим, что случайная величина X распределена по нормальному закону с плотностью вероятности
Случайная величина Y распределена по равномерному закону в интервале от a до b:
если a # y # b; если a < y < b.
Случайные величины X и Y независимы. Необходимо определить плотность распределения случайной величины Z, являющейся суммой этих величин:
66
Z = X + Y.
Применяя формулу (10.5 ) для композиции двух распределений, получим
Учитывая то, что плотность распределения f (y) равна нулю в пределах от 2` до a и от b до +`, плотность распределения f (z) примет вид:
(10.54)
Формально подынтегральная функция есть нормальная плотность распределения с математическим ожиданием z 2 mx и стандартным отклонением sx, а интеграл представляет собой вероятность попадания случайной величины Z на интервал (a, b). Используя, например, табличную функцию Лапласа, выражение для этой вероятности запишем в виде
Тогда плотность распределения f (z) примет вид:
(10.55)
Для удобства проведения анализа плотности (10.55) рас-
смотрим частный случай: mx = my = 0; b 2 a = 2l, т. е. a = 2l и b = +l. Тогда формула (10.55) примет вид
Если обозначить  и
и  , то
, то
(10.56)

При фиксированных значениях l0 с использованием таблицы функции Лапласа можно построить графики плотности f (z0). При l0 = 0, 1, 2, такие графики приведены на рис. 10. .
Из графиков видно, что чем больше l0, тем сильнее плотность композиции нормального и равномерного распределений отличается от нормального. Для наглядности на рис. 10. штриховой линией показана плотность нормального распределения
(при l0 = 0).
При сравнительно небольших l0 кривые плотности f (z0) имеют вид кривых нормального распределения, при больших значениях l0 кривые композиции становятся плосковершинными.
f(z0 ) |
|
0 = 0 |
|
0 =1 |
0 |
= 2 |
|
0 = |
0 |
z0 |
Рис. 10.3. Влияние величины l0 на вид кривых |
нормального распределения |
Поскольку  ,а
,а  , то
, то  . Отсюда видно, что
. Отсюда видно, что
вид плотности композиции нормального и равномерного распределений целиком и полностью определяется соотношением характеристик рассеивания этих распределений.
При решении практических задач композицию нормального и равномерного распределений приближенно заменяют нормальным распределением, оставляя неизменными параметры композиции
где
mz = mx + my; 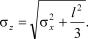
Однако следует заметить, что это справедливо только при небольших значениях l0. Погрешность от такой замены возрас-
10.7.2.Композициянормальныхраспределений
Часто при решении практических задач приходится находить композицию нормальных распределений (при исследовании точности стрельбы, точности приборов и т. п.).
Предположим, случайные величины X и Y независимы и распределены по нормальному закону с плотностями
и
Необходимо найти плотность распределения случайной величины
Z = X + Y.
Применяя общее выражение композиции двух распределений, получим
Если произвести преобразование в показателе степени подынтегрального выражения и замену переменной, то интеграл
сводится к табличному. Окончательное выражение композиции двух нормальных распределений получается в виде
(10.57)
где mz = mx + my.
Подробный вывод выражения плотности распределения f (z) можно найти в [5].
Таким образом, при композиции двух нормальных распределений получается снова нормальное распределение с математическим ожиданием mz = mx + my и стан-
Правила композиции двух нормальных распределений могут быть обобщены на случай произвольного числа независимых нормально распределенных случайных величин.
Предположим, что случайная величина
гдеX1, X2, …, Xn —независимыенормальнораспределенныеслу- чайныевеличинысматематическимиожиданиями
исредними квадратическими отклонениями  .
.
Вэтом случае Z также будет иметь нормальное распределение с математическим ожиданием
и средним квадратическим отклонением
Если величины Xi распределены по нормальному закону, но зависимы, то можно показать, что их сумма будет распределена также нормально с математическим ожиданием




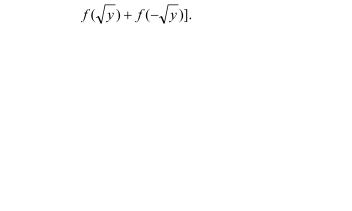







 и
и и
и  , то
, то
 , то
, то  . Отсюда видно, что
. Отсюда видно, что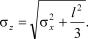
 .
.