(x1, x2, …, xk) — случайная ошибка результата наблюдения (эксперимента).
В общем случае распределение ошибки эксперимента зависит от комплекса условий. Считают, что ошибка эксперимента распределена по нормальному закону с математическим ожиданием, равным нулю (M[ (x1, x2, …, xk)] = 0 Поэтому
M[Y] = (x1, x2, …, xk)
Зависимость математического ожидания выходной переменной Y от входных переменных (x1, x2, …, xk) называется уравнением регрессии.
На выходе ОЭИ наряду с основной выходной переменной Y часто приходится контролировать группу неосновных выходных переменных V1, V2, …, Vk. На неосновные выходные переменные обычно налагаются ограничения.
K-мерное пространство, координатами которого являются контролируемые переменные, называется факторным пространством. Система ограничений на неосновные выходные переменные выделяет в факторном пространстве область эксперимента G.
Различают активные и пассивные эксперименты. Эксперимент будет активным, если имеется возможность не только контролировать входные переменные, но и управлять ими. В пассивном эксперименте исследователь не имеет возможности устанавливать значения входных переменных по своему усмотрению, т. е. управлять входными переменными.
11.3.сущностьвыборочногометода
Особенностью методов математической статистики является то, что выводы и заключения, полученные на основе этих методов, относятся не к отдельным испытаниям, которые были произведены, а представляют собой утверждения о вероятностных характеристиках исследуемого явления в целом [1, 12, 1 ]. Поэтому результат наблюдения в отдельном испытании следует рассматривать как один из возможных исходов, кото-




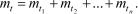
 . Требуется определить среднее время безотказной работы системы.
. Требуется определить среднее время безотказной работы системы.
