
где  ,
,  — оценки математических ожиданий случайных переменных X и Y.
— оценки математических ожиданий случайных переменных X и Y.
По полученным оценкам 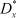 и
и  необходимо вынести суждение о равенстве истинных значений дисперсий Dx и Dy, т. е. проверить нулевую гипотезу H0: Dx = Dy.
необходимо вынести суждение о равенстве истинных значений дисперсий Dx и Dy, т. е. проверить нулевую гипотезу H0: Dx = Dy.
Если нулевая гипотеза будет справедлива, то это означает, что выборочные оценки  и
и  представляют собой оценки одной и той же дисперсии, а их различие обусловлено случайными причинами. В противном случае различие дисперсий существенно.
представляют собой оценки одной и той же дисперсии, а их различие обусловлено случайными причинами. В противном случае различие дисперсий существенно.
В качестве показателя согласованности проверки нулевой гипотезы о равенстве дисперсий принимают случайную величину
(1 .2 )
Показатель согласованности (1 .2 ) имеет распределение Фишера (F-распределение) с числами степеней свободы k1 = n1 2 1 и k2 = n2 2 1. Известно, что распределение Фишера зависит только от значений чисел степеней свободы и не зависит от других параметров. Плотность распределения Фишера показана на рис. 1 .6.
Для распределения Фишера составлена таблица значений up, удовлетворяющих равенству
(1 .24)
при различных комбинациях k1, k2 и значениях вероятности P, равных 0,01 и 0,05 (табл.14 приложения).

2. Вычисляют значение показателя согласованности по формуле (1 .25) или (1 .26) в зависимости от соотношения оценок дисперсий.
. Задают уровень значимости и находят по таблице вероятностей Фишера критическое значение показателя согласованности up. Входами в таблицу являются числа степеней
свободы k1, k1 и .
4. Проверяют справедливость нулевой гипотезы. Если выполняется неравенство u < up, то нулевую гипотезу принимают. В противном случае ее отклоняют как несправедливую.
Показатель согласованности (1 .2 ) можно использовать при сравнении дисперсий и в том случае, когда одна из них известна, т. е. для нее найдена не оценка, а точное значение.
При этом число степеней свободы закона распределения Фишера в числителе или знаменателе ПС следует устремить к бесконечности. В остальном, методика проверки гипотезы остается прежней.
Пример13.3.По результатам измерений при стендовых испытаниях десяти ЖРД определены числовые характеристики секундного расхода окислителя, значения которых оказались равными:
 кг/с и
кг/с и  кг/с.
кг/с.
При летных испытаниях десяти ракет с двигателями той же партии получены значения числовых характеристик:
 кг/с и
кг/с и  кг/с.
кг/с.
Требуется установить, изменяются ли действительные значения числовых характеристик в зависимости от того, в каких условиях работают двигатели (на стенде или в полете), если для измерения секундного расхода при стендовых и летных испытаниях использовались однотипные датчики.
Решение
1. Проверяем гипотезу о равенстве средних квадратических отклонений (дисперсий) секундного расхода, окислителя, для чего:

а) принимаем уровень значимости ПС равным 0,1 и по таблице F-распределения при числах степеней свободы k1 = k2 = 9 и P = 0,05 находим критическое значение up = ,18;
б) по формуле (1 .25), заменяя в ней и на и , вычисляем значение ПС u, отвечающее результатам испытаний:
u = (2,1/1,9)2 = 1,22.
Поскольку вычисленное значение ПС оказывается в области допустимых значений при достаточно высоком уровне значимости, можно считать, что результаты испытаний не противоречат гипотезе о равенстве средних квадратических отклонений секундного расхода окислителя при работе двигателей на стенде и в полете.
2. Проверяем гипотезу о равенстве математических ожиданий секундного расхода окислителя. Для этого, принимая во внимание результаты проверки гипотезы о равенстве дисперсий, используем ПС вида (1 .21):
а) по формуле (1 .22) вычисляем число степеней свободы показателя согласованности
k = 10 + 10 2 2 = 18;
б) принимаем уровень значимости ПС равным 0,1 и по таблице распределения Стьюдента при числе степеней свободы k = 18 находим критическое значение ПС |u | = 1,7 4;
в) определяем значение ПС, отвечающее результатам испытаний
Сопоставляя вычисленное значение ПС с критическим, приходим к выводу о том, что результаты испытаний не противоречат гипотезе о равенстве математических ожиданий секундного расхода окислителя при работе двигателей на стенде и в полете.

13.4.Проверкагипотезметодомпоследовательногоанализа
13.4.1.Сущностьметодапоследовательногоанализа
Впунктах 1 .2 и 1 . были изложены методы проверки гипотез по классической схеме, когда все множество возможных значений ПС разбивалось на два подмножества (две области): область допустимых значений и критическую об-
ласть (рис. 1 .8) [2].
Область допутимых |
Критическая |
значений |
область |
u u
Рис. 13.8
Решение о принятии или отклонении нулевой гипотезы принимается в зависимости от того, в какую область попало вычисленное по результатам испытаний значение ПС.
Классическим методам присущи два недостатка:
при малых объемах выборок принятие решения связано со значительной долей риска. Это обусловлено тем, что при уменьшении объема выборок увеличиваются вероятности ошибок первого и второго рода;
не существует подходов к обоснованию оптимальных объемов выборок, что затрудняет планирование и проведение экспериментов.
Метод последовательного анализа, разработанный А. Вальдом в некоторой степени свободен от этих недостатков. В отличие от классических методов в методе последовательного анализа вводится еще одна область — область продолжения испытаний (рис. 1 .9).
При попадании значения ПС в эту область принимается решение на необходимость проведения еще одного испытания. Испытания проводятся до тех пор, пока не будет приня-

Область Область Критическая
принятия продолжения область гипотезы испытаний
uA uB
Рис. 13.9
то решение на принятие или отклонение нулевой гипотезы. Число испытаний в методе последовательного анализа заранее не фиксируется. Оно зависит от конкретных полученных результатов испытаний, т. е. число испытаний является случайным.
Предпочтительными критериями принятия или отклонения нулевой гипотезы должны быть такие, чтобы при фиксированных вероятностях ошибок первого и второго рода обеспечивался минимум математического ожидания необходимого объема выборки. При использовании таких критериев метод последовательного анализа оказывается более экономичным по сравнению с классическим, так как в среднем требует для реализации меньшего числа испытаний.
При проверке гипотез методом последовательного анализа выделяют два этапа:
выбирают показатель согласованности u(n);
устанавливают решающее правило, в соответствии с которым после каждого испытания принимают одно из трех решений:
– нулевую гипотезу принять;
– нулевую гипотезу отклонить;
– провести еще одно испытание.
В качестве показателя согласованности при проверке гипотез данным методом принимают предложенный Вальдом последовательный показатель отношения вероятностей
(1 .27)

где P0n — вероятность появления результатов испытаний x1, x2, …, xn при условии справедливости проверяемой гипотезы;
P1n — вероятность появления этих результатов при условии, что проверяемая гипотеза неверна.
Проверяемая гипотеза принимается, если после n-го испытания выполняется условие
(1 .28)
или отклоняется, если окажется, что
(1 .29)
Если же вычисленное значение показателя согласованности после n-го испытания будет удовлетворять неравенству
(1 . 0)
то проводят еще одно испытание. После проведения испытания вычисляют новое значение ПС и проверяют неравенства
(1 .28–1 . 0).
Такой пошаговый процесс проверки гипотезы продолжают до тех пор, пока не будет принято решение: проверяемая гипотеза принимается либо отклоняется.
Метод последовательного анализа в окончательном виде разработан для решения лишь отдельных задач статистической проверки гипотез. Рассмотрим некоторые из этих задач.
13.4.2.Проверкагипотезыовероятностинаступлениясобытия
Решение данной задачи рассмотрим на примере контроля качества готовой продукции по доле в ней дефектных изделий. Из партии готовой продукции по одному извлекают изделие и подвергают контролю. Изделие может оказаться годным или дефектным. Совокупность результатов испытаний за n шагов можно описать числом m дефектных изделий среди n подверг-
нутых контролю. Вероятность извлечения дефектного изделия из партии при большом ее объеме численно равна доле таких изделий в партии.
Введем обозначения:
P0 — наибольшая доля дефектных изделий в партии, при которой партия считается еще годной;
P1 — наименьшая доля дефектных изделий, при которой она считается уже негодной.
Последовательный показатель отношения вероятностей после n-го шага будет определяться выражением
(1 . 1)
С учетом (1 . 1) неравенства (1 .28)–(1 . 0) запишем в следующем виде:
Прологарифмировав эти выражения, получим
(1 . 2)
где
(1 . )

(1 . 4)
Значения an и rn, которые принято называть приемочным и браковочным числами, при фиксированных P0, P1, и b зависят только от n и могут быть вычислены заранее.
На практике решение такого типа задач обычно производят графически. В прямоугольной системе координат по оси абсцисс откладывают номер шага испытания n, а по оси ординат — число бракованных изделий m, появившихся после n испытаний. Перед проведением испытаний рассчитывают коэффициенты уравнений (1 . ) и (1 . 4) и проводят на графике соответствующие прямые an и rn (рис. 1 .10).
|
m |
Область |
|
6 |
отклонения H0 |
|
5 |
Область |
|
4 |
|
проведения |
|
|
испытаний |
|
|
|
2 |
Область |
|
принятия H0 |
|
1 |
|
|
|
0 1 2 4 5 6 7 8 9 10 n |
|
|
Рис. 13.10 |
Эти прямые выделяют на плоскости три области: область принятия гипотезы H0; область отклонения гипотезы H0; область продолжения испытаний.
При испытании после каждого его шага на график наносят точку с координатами (n, m). В зависимости от того, в какую область попала точка, проверяемую гипотезу либо принимают, либо отклоняют, либо продолжают испытание.
На рис. 1 .10 представлен случай, когда гипотеза после пятого шага испытаний оказалась принятой.



 ,
,  — оценки математических ожиданий случайных переменных
— оценки математических ожиданий случайных переменных 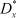 и
и  необходимо вынести суждение о равенстве истинных значений дисперсий
необходимо вынести суждение о равенстве истинных значений дисперсий  и
и  представляют собой оценки одной и той же дисперсии, а их различие обусловлено случайными причинами. В противном случае различие дисперсий существенно.
представляют собой оценки одной и той же дисперсии, а их различие обусловлено случайными причинами. В противном случае различие дисперсий существенно.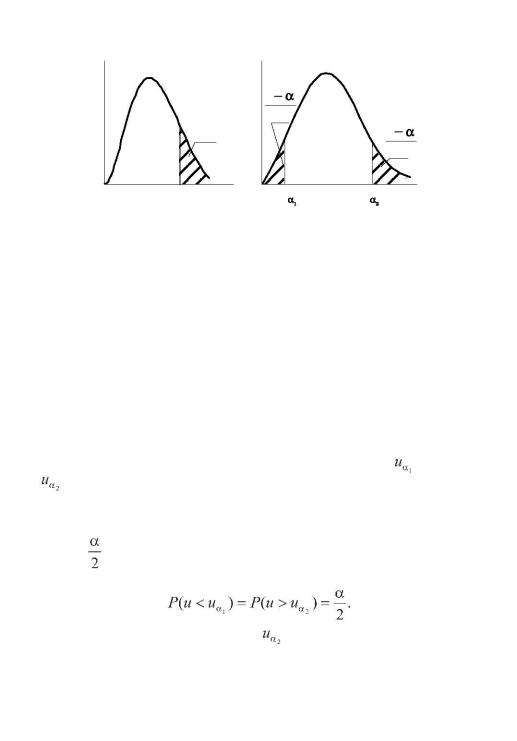


 кг
кг кг
кг кг
кг кг
кг




