Если s— стандартное отклонение кругового рассеивания точек попадания относительно точки прицеливания, то  и
и
при r # 0,
(9.67)
при r > 0.
Функция распределения F(r) случайной величины R, подчиняющейся закону Релея, определяется равенством
при r # 0,
(9.68)
при r > 0,
а основные числовые характеристики mr и Dr вычисляют по формулам:
(9.69)
(9.70)
Графики плотности и функции распределения изображе-
ны на рис. 9.29 и 9. 0.
гамма-распределение
Случайная величина X имеет гамма-распределение, если плотность распределения определяется выражением

при x # 0,
(9.71)
при x > 0,
где G( ) — гамма-функция;
и b — параметры распределения (b > 0).
В частном случае, если параметр принимает лишь целочисленные значения k = 0, 1, 2, …
G(k + 1) = kG(k) = k!
и выражение для плотности распределения при x > 0 может быть переписано в виде
(9.72)
Для гамма-распределения основные числовые характеристики — математическое ожидание и дисперсию — определяют по формулам:
m |
x |
= b( + 1), D |
x |
= b2( + 1). |
(9.7 ) |
|
|
|
|
Гамма-распределение находит широкое применение в теории надежности. Оно используется при исследовании надежности аппаратуры в период ее приработки и работы в форсированных режимах.
Если плотность гамма-распределения определяется выражением (9.72), то говорят, что случайная величина X имеет распределение Эрланга k-го порядка. Показательное распределение является распределением Эрланга нулевого порядка. Если в выражении (9.72) положить k = 0, получим (9.40).
Одним из частных случаев гамма-распределения является x2 (хи-квадрат)-распределение с k степенями свободы, для которого плотность распределения определяется выражением
при x # 0,
(9.74)
при x > 0.

Формула (9.74) следует из (9.71) при b = 2, , (k = 1, 2, , …).
Если случайная величина X подчиняется x2-распределе- нию, то из (9.7 ) следует, что mx = k, Dx = 2k.
x2-распределение широко используется при статистической обработке и анализе результатов испытаний образцов про-
дукции [1, 10, 14].
РаспределениеСтьюдента
Случайная величина X имеет распределение Стьюдента, если плотность распределения определяется выражением
(9.75)
где k — целочисленный параметр, называемый числом степеней свободы.
Данное распределение широко используется при обработке результатов испытаний образцов продукции.
При неограниченном увеличении k (k > 0) плотность распределения Стьюдента приближается к плотности нормального распределения, т. е. для распределения Стьюдента нормальное распределение является предельным.
9.5.распределениеслучайноговектора
Распределения векторных случайных величин представляются теми же основными формами, что и распределения скалярных. В дальнейшем ограничимся рассмотрением этих форм применительно лишь к двумерному случайному вектору (системе двух случайных величин).
Функция вероятности используется только для случайных векторов с дискретными компонентами и обычно задается таблицей, где указываются возможные значения xi и yi компонент X и Y случайного вектора {X, Y}, а также вероятности p(xi, yi) всех пар этих значений (табл. 9. ).

Очевидно, что при этом
|
|
|
|
|
|
|
Таблица 9.3 |
|
|
|
|
|
|
|
|
|
y |
xi |
x1 |
x2 |
… |
xi |
… |
|
xn |
|
j |
|
|
|
|
|
|
|
|
y1 |
p(x1, y1) |
p(x2, y1) |
… |
p(xi, y1) |
… |
|
p(xn, y1) |
|
y2 |
p(x1, y2) |
p(x2, y2) |
… |
p(xi, y2) |
… |
|
p(xn, y2) |
|
… |
… |
… |
… |
… |
… |
|
… |
|
|
|
|
|
|
|
|
|
|
yj |
p(x1, yj) |
p(x2, yj) |
… |
p(xi, yj) |
… |
|
p(xn, yj) |
|
… |
… |
… |
… |
… |
… |
|
… |
|
|
|
|
|
|
|
|
|
|
ym |
p(x1, ym) |
p(x2, ym) |
… |
p(xi, ym) |
… |
|
p(xn, ym) |
Функцией распределения двумерного случайного вектора {X, Y} называется функция F(x, y) двух аргументов x и y, которая при каждой комбинации их значений задает вероятность совместного выполнения двух неравенств: X < x и Y < y, т. е.
|
|
F(x, y) = P(X < x, y < Y). |
|
(9.76) |
|
Таким образом, функция распределения F(x, y) задает ве- |
|
роятность того, что точка со случайными координатами X и Y |
|
(случайная точка {X, Y} окажется где- |
|
y |
|
либо в пределах бесконечного квад- |
|
|
|
|
|
ранта плоскости x0y, правая верши- |
|
(x, y) |
|
на которого имеет координаты x и y |
|
|
|
(рис. 9. 1). |
|
|
|
|
|
Функция |
распределения |
слу- |
|
|
|
чайного вектора {X, Y} с дискретными |
0 |
x |
|
компонентами связана с вероятнос- |
|
|
|
|
тями p(xi, yj) комбинацией их всевоз- |
Рис. 9.31 |
|
|
можных значений соотношением |
|
|
|
|
|
|
(9.77)
Она представляется в трехмерном пространстве ступенчатой (для случайного вектора {X, Y} с дискретными компонентами) или гладкой поверхностью (для случайного вектора с непрерывными компонентами).
Основными свойствами функции распределения двумерного случайного вектора являются следующие:
1. 0 # F(x, y) # 1, поскольку функция F(x, y) представляется вероятностями.
2. 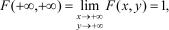
(9.78)
в чем нетрудно убедиться, обращаясь к рис. 9. 1.
. Функция распределения F(x, y) — неубывающая функция каждого из своих аргументов
F(x2, y) $ F(x1, y), если x2 > x1, F(x, y2) $ F(x, y1), если y2 > y1,
F(x2, y2) $ F(x1, y1), если x2 > x1 или y2 > y1,
yчто опять-таки следует из рис. 9. 1.
|
|
x |
|
4. Вероятность |
попадания |
|
|
|
y |
случайной точки {X, Y} в прямо- |
|
|
|
угольник, стороны которого парал- |
|
y |
|
|
лельны осям координат 0x, 0y (рис. |
|
|
|
9. 2), равна алгебраической сумме |
|
0 |
x |
x |
|
значений функции распределения |
|
|
|
|
|
|
|
|
F(x, y) в вершинах этого прямо- |
|
Рис. 9.32 |
|
угольника |
|
|
|
|
|

P(x # X < x + Dx, y # Y < y + Dy) = |
|
= F(x + Dx, y + Dy) 2 F(x + Dx, y) 2 |
|
2 F(x, y + Dy) + F(x, y). |
(9.79) |
Отсюда следует, что вероятность совпадения случайной точки {X, Y} с любой точкой плоскости, как и вероятность ее попадания на любую линию этой плоскости, равна нулю.
Плотностью распределения двумерного случайного вектора {X, Y} называется функция f (x, y) аргументов, которая определяется следующим образом:
(9.80)
т. е. является пределом отношения вероятности попадания случайной точки {X, Y} в прямоугольник со сторонами Dx и Dy, примыкающий к точке (x, y), когда оба его размера стремятся к нулю (если такой предел существует).
С учетом соотношения (9.79) равенство (9.80) можно представить в виде
(9.81)
что обеспечивает возможность нахождения плотности f (x, y), если функция распределения F(x, y) задана.
Геометрически плотность распределения f (x, y) представляется поверхностью в трехмерном пространстве и используется применительно только к случайным векторам с непрерывными компонентами.
Плотность распределения двумерного случайного вектора имеет следующие основные свойства.
1. f (x, y) $ 0 как предел отношения неотрицательной величины к положительной.
что непосредственно вытекает из соотношения (9.81).
. Вероятность попадания случайной точки {X, Y} в какуюлибо область G на плоскости x0y определяется равенством
(9.8 )
т. е. численно равна объему под поверхностью f (x, y) над этой областью (рис. 9. ).
f x, y
0
Рис. 9.33
Отсюда следует, что с точностью до бесконечно малых высших порядков вероятность попадания случайной точки {X, Y} в бесконечно малую окрестность точки (x, y) P(x # X < x + Dx, y # Y < y + Dy) на плоскости x0y определяется равенством
P(x # X < x + Dx, y # Y < y + Dy) = f (x, y)dxdy, |
(9.84) |
правую часть которого называют элементом вероятности.
4.  как вероятность достоверного события,
как вероятность достоверного события,
так что весь объем под поверхностью плотности распределения равен единице.
Размерность плотности f (x, y) обратна произведению размерностей компонент X и Y случайного вектора, что полезно иметь в виду при решении практических задач, связанных с нахождением плотностей распределения.
Функцию и плотность распределения двумерного случайного вектора {X, Y} принято задавать на всей плоскости x0y.
27

9.6.частныеиусловныераспределениякомпонент случайноговектора
9.6.1.Частныераспределения
Распределение одной или нескольких компонент, входящих в случайный вектор (систему случайных величин), называют частным распределением.
Частные распределения случайных величин, составляющих систему, часто используются при решении практических задач. Например, если рассматривается система трех случайных величин {X, Y, Z}, то помимо частных распределений отдельных случайных величин рассматривают и частные распределения различных пар случайных величин {X, Y}, {X, Z}, {Y, Z}.
В дальнейшем рассмотрим частные распределения для системы двух случайных величин.
При известном распределении вектора {X, Y} частные распределения определяются следующим образом. Предположим компоненты X и Y — дискретные случайные величины, совместное распределение которых задано табл. 9. . Вероятности p(xi), p(yi) возможных значений компонент X и Y, которые представляют частные распределения каждой из них, определяются выражениями
(9.85)
Таким образом, вероятности возможных значений компоненты X получаются суммированием записанных в табл. 9. чисел по строкам, а вероятности возможных значений компоненты Y — суммированием этих чисел по строкам.
Если распределение случайного вектора {X, Y} задано функцией распределения, то с учетом свойства функции распределения частные функции распределения F(x) и F(y) следует определять из соотношений

(9.86)
Для вектора с непрерывными компонентами плотности f (x) и f (y) соответствующих частных распределений могут быть получены на основе равенства (9.11)
 и
и 
В случае если распределение случайного вектора {X, Y} задано плотностью f (x, y), то плотности f (x) и f (y) частных распределений его компонент могут быть получены из соотношений
(9.87)
Выражения (9.87) получены исходя из свойств плотности и функции распределения (равенства 9.81 и 9.82).
Из соотношений (9.87) следует, что геометрически плотность f (x) частного распределения компоненты X при каждом значении аргумента x представляется площадью вертикального сечения фигуры, ограниченной поверхностью f (x, y), причем секущая плоскость проходит через точку x перпендикулярно оси 0x (рис. 9. ). Аналогичную геометрическую интерпретацию дают и плотности f (y) частного распределения компоненты Y.
Пример 9.4. Мобильная точечная цель свободно маневрирует на участке местности, который представляется кругом радиуса R. Информация о фактическом положении цели отсутствует. Найти распределения ее прямоугольных координат относительно центра области маневрирования.
Решение
По условиям задачи положение цели в произвольный момент времени описывается двумерным случайным вектором,
компонентами которого являются ее текущие координаты X и Y в заданной системе координат. Плотность f (x, y) распределения этого случайного вектора может быть получена следующим образом. Поскольку информация о фактическом текущем положении цели отсутствует, то нахождение ее в окрестности любой точки круга радиуса R является равновозможным. Используя геометрический способ определения вероятности, получим
Согласно соотношению (9.80) распределение случайного вектора {X, Y} описывается плотностью
при x2 + y2 > R2,
представленной на рис. 9. 4 (равномерное распределение в круге радиуса R с центром в начале координат).
Плотность f (x, y) отлична от нуля для любого значения x
при
(рис. 9. 5), а для любого значения y при
|
f(x, y) |
|
y |
|
|
|
R2 |
x2 |
|
|
|
|
|
|
|
R |
|
R |
|
|
|
1 |
|
|
|
|
R2 |
|
|
x |
x |
|
|
|
0 |
|
0 |
|
|
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
Рис. 9.34 |
|
Рис. 9.35 |
|
|








 как вероятность достоверного события,
как вероятность достоверного события,



 и
и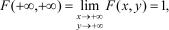
 и
и 