
f u/H1
Рис. 13.2
Для уменьшения вероятности ошибки при принятии гипотезы критическую границу необходимо выбирать таким образом, чтобы сумма вероятностей ошибок первого и второго рода была минимальной. В случае, если показатель согласованности распределен по нормальному закону, то минимум суммы вероятностей ошибок и b достигается при выборе критической границы в абсциссе точки пересечения кривых плотностей распределения f (u/H0) и f (u/H1) (на рис. 1 .2 точка  ). Однако, не всегда такой подход к выбору критической границы u является целесообразным.
). Однако, не всегда такой подход к выбору критической границы u является целесообразным.
Часто при решении практических задач при выборе u исходят из анализа последствий от неверно принятого решения (“тяжести” последствий ошибок первого и второго рода для конкретной задачи). Например, если ошибка первого рода повлечет большие потери, а второго рода — малые, то целесообразно назначить возможно меньшее значение .
Критерий проверки гипотезы принято характеризовать мощностью показателя согласованности. Под мощностью по-
казателя согласованности понимают вероятность попадания ПС в критическую область, при условии что справедлива альтернативная гипотеза H1. В соответствии с данным определением можно записать

Из данного выражения видно, что мощность ПС это есть вероятность того, что не будет допущена ошибка второго рода.
Таким образом, для уменьшения ошибки второго рода критическую область надо выбирать так, чтобы мощность ПС при заданном уровне значимости была максимальной.
Следуетотметить,чтомощностьПСпозволяетобоснованно подойти к выбору односторонних критических областей. Если характер альтернативной гипотезы неясен, то целесообразно в качестве критической выбирать двустороннюю симметричную область.
Для того чтобы одновременно уменьшить ошибки первого и второго рода, необходимо увеличивать объем выборки, по результатам которой проверяют гипотезу.
13.2.Методыпроверкигипотезозаконахраспределения
13.2.1.Постановказадачи
При обосновании закона распределения случайной переменной по результатам испытаний обычно решают две задачи:
1.Задача выравнивания (сглаживания) полученного при испытании статистического ряда. При решении данной задачи подбирают теоретическую кривую распределения, которая выражает лишь существенные черты статистического распределения.
2.Задача проверки гипотезы о законе распределения. В результатерешенияустанавливаютпричинырасхождениямежду подобранной теоретической кривой распределения и статистическим распределением. Расхождение может быть обусловлено либо случайными отклонениями, либо тем, что подобранная кривая плохо описывает статистическое распределение.
Задача выравнивания заключается в том, чтобы подобрать теоретическую кривую распределения, которая с той или иной

точки зрения наилучшим образом описывает данное статистическое распределение. Выбранный в результате решения данной задачи теоретический закон распределения принимается в качестве нулевой гипотезы. Для ее решения используют метод моментов, систему кривых К. Пирсона, систему кривых Н. А. Бородачева и ряд других методов.
Для выбора нулевой гипотезы может быть использована следующая методика. По результатам испытаний находят оценки коэффициентов асимметрии  и эксцесса
и эксцесса 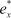
(1 .1)
где  — оценка стандартного отклонения исследуемой случайной переменной X,
— оценка стандартного отклонения исследуемой случайной переменной X,
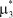
 — оценка центрального момента третьего (четвертого) порядка случайной переменной X,
— оценка центрального момента третьего (четвертого) порядка случайной переменной X,
Доказано, что каждому закону распределения соответствует вполне определенное соотношение между коэффициентами асимметрии и эксцесса. На основе данного свойства строят диаграмму, на которой могут быть выделены точки, прямые и области, отвечающие соответствующему распределению. Такая диаграмма показана на рис. 1 . .
С помощью этой диаграммы можно приближенно определить гипотетический закон распределения, который следует выдвигать в качестве нулевой гипотезы. Для этого на диаграмму наносится точка с координатами  , которые получены по формулам (1 .1). Если она окажется вблизи от точки, прямой или области, соответствующей одному из распределений, то его и следует выдвигать в качестве нулевой гипотезы.
, которые получены по формулам (1 .1). Если она окажется вблизи от точки, прямой или области, соответствующей одному из распределений, то его и следует выдвигать в качестве нулевой гипотезы.

F*(x), F(x) — соответственно статистическая и теоретическая функции распределения исследуемой случайной переменной X.
Независимо от вида закона распределения случайной переменной X функция распределения ПС при n → ` имеет вид
(1 .5)
где k — число степеней свободы;
u — показатель согласованности.
В качестве критической области используется правосторонняя область, границу u которой определяют из условия
= P(u $ u ) = 1 2 P(u < u ) = 1 2 F(u = ua),
т. е. она равна квантилю случайной величины u при аргументе
где F21(*) — функция, обратная функции распределения показателя согласованности.
Для определения u в соответствии с формулой (1 .6) составлена специальная табл. 1 .1.
|
|
|
|
|
Таблица 13.1 |
|
|
|
|
|
|
|
|
0,5 |
0,1 |
0,05 |
0,01 |
|
0,001 |
u |
0,828 |
1,224 |
1,258 |
1,627 |
|
1,950 |
|
|
|
|
|
|
|
Проверка нулевой гипотезы методом А. Н. Колмогорова производится следующим образом.
1.По результатам испытаний строят статистическую функцию распределения F*(x) (рис. 1 .4).
2.На том же графике строят функцию F(x) теоретического закона распределения, принятого в качестве нулевой гипотезы.
. По графику определяют максимальную величину модуля разности ординат статистической и теоретической функций распределения и вычисляют значение показателя согласованности u по формуле (1 .4).

F(x) F*(x) |
|
1,0 |
|
|
F(x) |
|
F*(x) |
0 |
x |
|
Рис. 13.4 |
4. Назначаютуровеньзначимостикритерия ипотабл. 1 .1 определяют критическое значение показателя согласованнос-
ти u .
5. Проверяют справедливость выдвинутой гипотезы H0. Если выполняется неравенство u $ u , то гипотезу H0 бракуют, в противном случае делают вывод, что результаты испытаний не противоречат гипотезе о том, что исследуемая случайная переменная X подчинена закону распределения с функцией F(x).
Достоинством метода А. Н. Колмогорова является его простота и отсутствие сложных расчетов. Однако для его применения необходимо знать не только вид теоретического закона распределения, но и его параметры. Кроме того, метод учитывает только максимальное отклонение статистической функции распределения от теоретической функции, а не закон изменения отклонения по всему размаху выборки.
Проверкагипотезметодомн.в.смирнова
При проверке гипотезы данным методом в качестве меры рассогласования теоретического и статистического законов распределения принимается функция разности статистической и теоретической функции распределения. В качестве показателя согласованности используется среднее значение разности по всей области определения функции распределения.

Если исследуемая случайная переменная X непрерывного типа, то ПС определяется выражением
(1 .7)
Для дискретной случайной величины выражение (1 .7) запишется в виде
(1 .8)
где Pi — вероятность появления в выборке значения xi.
На практике для удобства вычислений выражение (1 .8) преобразуют к виду
(1 .9)
Значения критической границы u в зависимости от уровня значимости критерия приведены в табл. 1 .2. Они рассчитываются в соответствии с законом распределения ПС по формуле
u = F21(1 2 ),
где F21(*) — функция, обратная функции распределения показателя согласованности.
|
|
|
|
|
Таблица 13.2 |
|
|
|
|
|
|
|
|
0,5 |
0,1 |
0,05 |
0,02 |
|
0,001 |
u |
0,118 |
0, 47 |
0,461 |
0,620 |
|
0,744 |
Проверка нулевой гипотезы методом Н. В. Смирнова производится в следующем порядке:
1.Вычисляют по результатам испытаний значение показателя согласованности u в соответствии с (1 .9).
2.Назначают уровень значимости и по таблице 1 .2 опре-
деляют значение границы критической области u .
. Проверяют справедливость нулевой гипотезы H0. Если выполняется неравенство u > u , то гипотеза H0 отклоняется.

Если же u # u , то делается вывод о том, что результаты испытания не противоречат гипотезе о распределении переменной X по предполагаемому закону с функцией F(x).
Проверкагипотезметодомк.Пирсона
В качестве меры расхождения теоретического и статистического законов распределения принята сумма квадратов разностеймеждучастотойивероятностьюпопаданияисследуемой случайной переменной X в интервалы, на которые разбивается множество возможных значений этой переменной
(1 .10)
где m — число интервалов, на которые разбивается множество возможных значений при построении статистической функции распределения.
Коэффициенты Cj вводятся для того, чтобы учесть неравнозначность абсолютных значений разностей  при различных значениях вероятности Pj. Поскольку одно и то же значение разности
при различных значениях вероятности Pj. Поскольку одно и то же значение разности  является малозначимым при большой вероятности Pj и представляет собой заметную величину, когда Pj мала.
является малозначимым при большой вероятности Pj и представляет собой заметную величину, когда Pj мала.
К. Пирсон показал, что если коэффициенты Cj определять в соответствии с выражением
то при большом объеме выборки закон распределения случайной величины u, определяемой формулой (1 .10), практически не зависит от вида закона распределения случайной переменной Xи объема выборки n, а зависит только от числа интервалов m. При этом при увеличении m закон распределения случайной величины u приближается к x2 (хи-квадрат)-распределению с числом степеней свободы k = m 2 1.
На практике в качестве ПС используют и случайную величину
(1 .11)

гдевал; nj — число результатов испытаний, попавших в j-й интер-
Pj — вероятность попадания результата испытания в j-й интервал при теоретическом законе распределения исследуемой переменной X.
Взависимости от формы представления результатов испы-
таний (исходными данными для проверки гипотезы являются  или nj) в качестве ПС принимают выражение (1 .10) либо (1 .11).
или nj) в качестве ПС принимают выражение (1 .10) либо (1 .11).
Вдальнейшем будем рассматривать ПС вида (1 .11).
Если параметры теоретического закона, который принят в качестве нулевой гипотезы, неизвестны, то вычисление вероятностей Pj не представляется возможным. Оказывается, что если при определении этих вероятностей вместо неизвестных значений параметров теоретического распределения подставить соответствующие их оценки , полученные по результатам испытаний, то случайная величина
(1 .12)
при n → ` также будет иметь x2-распределение, но с числом степеней свободы
где s — число неизвестных параметров теоретического закона распределения.
Так, например, для нормального закона распределения s = 2 (параметры — математическое ожидание и дисперсия), для показательного — s = 1 (параметр — коэффициент l) и т. д.
Таким образом, для проверки нулевой гипотезы в качестве показателя согласованности принимают случайную величину (1 .12). При этом неизвестные значения параметров теоретического распределения определяют с помощью статистических оценок.
При группировании результатов испытаний по интервалам для нахождения оценок математического ожидания и дисперсии обычно используют формулы



 ). Однако, не всегда такой подход к выбору критической границы
). Однако, не всегда такой подход к выбору критической границы 

 и эксцесса
и эксцесса 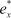
 — оценка стандартного отклонения исследуемой случайной переменной
— оценка стандартного отклонения исследуемой случайной переменной 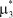
 — оценка центрального момента третьего (четвертого) порядка случайной переменной
— оценка центрального момента третьего (четвертого) порядка случайной переменной  , которые получены по формулам (1 .1). Если она окажется вблизи от точки, прямой или области, соответствующей одному из распределений, то его и следует выдвигать в качестве нулевой гипотезы.
, которые получены по формулам (1 .1). Если она окажется вблизи от точки, прямой или области, соответствующей одному из распределений, то его и следует выдвигать в качестве нулевой гипотезы.





 при различных значениях вероятности
при различных значениях вероятности  является малозначимым при большой вероятности
является малозначимым при большой вероятности 
 или
или