
пешных» реализаций, а не хранить результаты всех испытаний. Для оценки математического ожидания накапливают сумму возможных значений случайной величины Xi: i = 1, 2, …, n, которые она принимает в различных реализациях.
Непосредственное вычисление оценки дисперсии по формуле (12.15) нерационально, так как среднее значение  изменяется в процессе накапливания значений xi. Это приводит к необходимости запоминания всех n значений xi. Поэтому более рационально организовать фиксацию результатов моделирования для вычисления оценки дисперсии с использованием следующей формулы [1, 10, 1 ]:
изменяется в процессе накапливания значений xi. Это приводит к необходимости запоминания всех n значений xi. Поэтому более рационально организовать фиксацию результатов моделирования для вычисления оценки дисперсии с использованием следующей формулы [1, 10, 1 ]:
Это значит, что для вычисления оценки дисперсии необходимо и достаточно накапливать две суммы: xi и их квадратов  .
.
12.4.4.Определениечисловыххарактеристикслучайныхвеличин прибольшомобъемевыборки
При очень большом числе результатов измерений (несколько десятков или сотен) определение числовых характеристик случайных величин с помощью оценок (12.10) и (12.15) требует громоздких вычислений. Поэтому в таких случаях часто используют упрощенный способ решения задачи. Сущность его заключается в том, что результаты измерений группируют по интервалам, т. е. представляют их в виде статистического ряда, а искомые числовые характеристики определяют с помощью оценок следующего вида:
(12.16)
где m — число интервалов;

— частота попадания результатов измерений в j-й интервал;
xcpj — координата середины j-го интервала.
Выражения (12.16) аналогичны выражениям (12.10), (12.15) и (9.16), (9.22), определяющим математическое ожидание и дисперсию дискретной случайной величины. Разница состоит только в том, что здесь вероятности заменены частотами, а математическое ожидание mx — статистическим средним  .
.
12.5.интервальноеоцениваниечисловыххарактеристик случайныхвеличин
12.5.1.Понятиедоверительнойвероятности
идоверительногоинтервала
При точечном оценивании получаются лишь приближенные значения искомых параметров. Степень рассеивания этих значений относительно истинных характеризуется дисперсиями (стандартными отклонениями) оценок. Однако знание этих дисперсий обычно оказывается недостаточным. Иногда требуется знать, насколько значение истинного параметра, полученное с помощью оценки при том или ином объеме выборки, отличается от истинного значения данного параметра, т. е. какой является ошибка:
(12.17)
Из равенства (12.17) видно, что величина погрешности  случайна, а истинное значение x неизвестно. Поэтому нельзя определить значение погрешности, даже зная оценку
случайна, а истинное значение x неизвестно. Поэтому нельзя определить значение погрешности, даже зная оценку  . Относительно погрешности
. Относительно погрешности  можно сделать суждение вероятностного характера. Такие суждения обычно делают на основе понятия доверительного интервала.
можно сделать суждение вероятностного характера. Такие суждения обычно делают на основе понятия доверительного интервала.
Под доверительным интервалом понимают случайный интервал, который с некоторой вероятностью накрывает истинное значение искомого параметра:
(12.18)

При интервальном оценивании решаются следующие основные задачи:
определение доверительного интервала при заданной доверительной вероятности и фиксированном числе испытаний;
определение доверительной вероятности при заданном доверительном интервале и фиксированном числе испытаний;
определение необходимого числа испытаний при заданных доверительной вероятности и доверительном интервале.
Решение указанных задач не вызывает затруднений, если
известен закон распределения случайной величины  Рассмотрим методы решения задач интервального оценивания при определении вероятности наступления случайного события, математического ожидания и стандартного отклонения случайной величины, которые наиболее часто используются в качестве характеристик вооружения и показателей эф-
Рассмотрим методы решения задач интервального оценивания при определении вероятности наступления случайного события, математического ожидания и стандартного отклонения случайной величины, которые наиболее часто используются в качестве характеристик вооружения и показателей эф-
фективности боевых действий.
Иногда в силу ограниченности априорных сведений об исследуемом процессе либо из-за сложности вероятностных расчетов установить закон распределения не удается. В этом случае вначале приходится выдвигать соответствующие гипотезы относительно закона распределения оценки и проводить их проверку.
12.5.2.Оцениваниевероятностинаступленияслучайногособытия
Как было показано в п. 12.4.1, частота P*, полученная по результатам n реализаций в соответствии с формулой (12.7), является эффективной оценкой вероятности P. В силу центральной предельной теоремы теории вероятностей (теоремы Ляпунова) при большом n распределение частоты P* описывается нормальным законом распределения с плотностью вероятности
(12.22)
При этом математическое ожидание и стандартное отклонение частоты определяются выражениями:
(12.2 )
Рассмотрим случайную величину
(12.24)
Поскольку случайная величина Y связана с частотой P* линейной зависимостью, то она также имеет нормальное распределение с математическим ожиданием, равным нулю, и дисперсией, равной единице, т. е. Y [ N(0,1). Поэтому при любом уровне вероятности справедливо соотношение
(12.25)
где  — аргумент табличной функции Лапласа, при ко-
— аргумент табличной функции Лапласа, при ко-
тором FT(y ) = . Неравенство
равносильно неравенству
или неравенству
Отсюда вытекает, что интервал
(12.26)
накрывает неизвестное значение P с вероятностью .
Таким образом, для определения доверительного интервала при заданной доверительной вероятности и фиксированном n необходимо:
по результатам n испытаний по формуле (12.7) получить значение частоты P*;
рассчитать значение стандартного отклонения
по доверительной вероятности из таблицы функции Лапласа (табл. 2 приложения) найти значение y ;
рассчитать границы доверительного интервала по фор-
муле (12.26).
Р |
P =P* +y |
P* |
|
|
1,0 |
|
|
|
|
P |
|
|
|
|
P* |
|
|
|
|
P |
|
P =P* |
y |
P* |
0 |
P* |
1,0 |
|
P* |
Рис. 12.8. Зависимость границ доверительного интервала для вероятности случайного события от значения частоты
На рис. 12.8 представлены зависимости границ доверительного интервала  и от значения оценки P* при фиксированных значениях и n. Поскольку при вычислении оценки стандартного отклонения по формуле (12.2 ) вместо неизвестного значения вероятности P подставляют ее оценку P*, полученную по результатам n испытаний, то оказывается случайным не только центр доверительного интервала, но и его длина.
и от значения оценки P* при фиксированных значениях и n. Поскольку при вычислении оценки стандартного отклонения по формуле (12.2 ) вместо неизвестного значения вероятности P подставляют ее оценку P*, полученную по результатам n испытаний, то оказывается случайным не только центр доверительного интервала, но и его длина.

Определение доверительной вероятности при заданном доверительном интервале gи фиксированном числе испытаний n производится в такой последовательности:
рассчитать значения оценок вероятности P* и стандартного отклонения ;
вычислить значение аргумента табличной функции Лапласа
(12.27)
по значению y из таблицы функции Лапласа найти вероятность .
Если требуемые точность g и достоверность оценивания вероятности P заданы, то необходимое для их обеспечения число испытаний nтр находится из уравнения (12.27):
(12.28)
где y находится из таблицы функции Лапласа по известной доверительной вероятности .
Из соотношения (12.28) видно, что при фиксированном значении необходимое число испытаний обратно пропорционально квадрату допустимой абсолютной погрешности g. Поэтому для определения вероятности P по частоте P* с достаточной точностью и достоверностью требуется большое число испытаний. В табл. 12.7 приведены необходимые значения числа испытаний nтр, обеспечивающие с доверительной вероятностью требуемую точность g оценивания различных значений вероятности P.
Из таблицы видно, что необходимое число испытаний растет не только с увеличением требуемой точности, но и с приближением истинного значения оцениваемой вероятности P к вероятности, равной 0,5. Это обусловлено тем, что дисперсия оценки P* достигает максимального значения, равного 0,25/n, именно при P = 0,5.
Поскольку в выражение (12.28) входит неизвестное значение вероятности P, то определение необходимого числа ис-
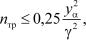
Таблица 12.7
требуемое число испытаний для оценивания вероятности с заданной точностью
Р |
|
|
g |
|
0,05 |
0,01 |
|
0,005 |
0,001 |
|
|
0,1 (0,9) |
1 9 |
458 |
|
1 8 0 |
45744 |
0,2 (0,8) |
246 |
6147 |
|
24587 |
614656 |
0, (0,7) |
2 |
8068 |
|
2270 |
8067 6 |
0,4 (0,6) |
69 |
9220 |
|
6880 |
921984 |
0,5 |
85 |
9604 |
|
8416 |
960400 |
пытаний nтр производят приближенно. Один из способов такого приближения состоит в оценке верхней границы необходимого числа испытаний на основе неравенства
которое получается с учетом того, что max{P(1 ] P)} = 0,25. Другой способ заключается в реализации соотношения
(12.28) путем последовательного уточнения частоты P* и n, начиная с некоторого ориентировочного значения числа испытаний n0. После проведения n0 испытаний это значение уточняют, заменяя в формуле (12.28) вероятность P полученным значением частоты P*. Если при этом окажется, что новое значение n1 не превышает n0, решение задачи заканчивается. Если же n1 > n0, то производят еще (n1 ] n0) испытаний, по результатам которых уточняют значение частоты, а по нему — значение необходимого числа испытаний. Этот процесс продолжается до тех пор, пока не будет обеспечена заданная точность определения вероятности P.
12.5.3.Оцениваниематематическогоожидания
При оценивании математического ожидания следует различать случаи большой (n > 0) и малой (n # 0)










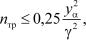

 изменяется в процессе накапливания значений
изменяется в процессе накапливания значений  .
. .
. случайна, а истинное значение
случайна, а истинное значение  . Относительно погрешности
. Относительно погрешности  можно сделать суждение вероятностного характера. Такие суждения обычно делают на основе понятия доверительного интервала.
можно сделать суждение вероятностного характера. Такие суждения обычно делают на основе понятия доверительного интервала. Рассмотрим методы решения задач интервального оценивания при определении вероятности наступления случайного события, математического ожидания и стандартного отклонения случайной величины, которые наиболее часто используются в качестве характеристик вооружения и показателей эф-
Рассмотрим методы решения задач интервального оценивания при определении вероятности наступления случайного события, математического ожидания и стандартного отклонения случайной величины, которые наиболее часто используются в качестве характеристик вооружения и показателей эф- — аргумент табличной функции Лапласа, при ко-
— аргумент табличной функции Лапласа, при ко- и от значения оценки
и от значения оценки