Вариант №7
1. В комплекте —12 деталей первого сорта и 6 —второго. Наудачу вынимаются 4 детали. Найти вероятность того, что среди них окажутся
3 детали первого сорта.
2. В урне 5 белых и 4 красных шара, одинаковых наощупь. Наудачу вынимаются 3 шара. Найти вероятность того, что среди извлеченных шаров будет не менее 2 красных.
3. Найти вероятность безотказной работы функциональной схемы,
┌─────┐ ┌─┤ 4 ├─┐ ┌─────┐ ┌─────┐ │ └─────┘ │ ┌──┤ 1 ├──┤ 2 ├──┐ ┌──┤ ├──┐ │ └─────┘ └─────┘ │ │ │ ┌─────┐ │ │ ┌─────┐ ──┤ ├──┤ └─┤ 5 ├─┘ ├──┤ 7 ├── │ ┌─────┐ │ │ └─────┘ │ └─────┘ └──────┤ 3 ├───────┘ │ │ └─────┘ │ ┌─────┐ │ └────┤ 6 ├────┘ └─────┘
состоящей из независимо работающих элементов, если вероятность работы каждого элемента равна 0,98.
4. Комплект состоит из 16‑ти деталей завода №1, 12‑ти деталей завода №2 и 22‑х деталей завода №3. Вероятности того, что деталь низкого качества соответственно равны 0,08 для первого завода, 0,06 —для второго завода и 0,1 для третьего. Найти вероятность того, что наудачу вынутая деталь из комплекта будет высокого качества.
5. Событие B появится в том случае, если событие A наступит не менее двух раз. Найти вероятность появления события B, если произведено шесть независимых испытаний, в каждом из которых вероятность появления события A равна 0,4.
6. Автобаза обслуживает 240 магазинов. От каждого из них заявка на автомашины на следующий день может поступить с вероятностью 0,4. Найти вероятность того, что поступит не более 110‑ти заявок; ровно 110 заявок.
7. Коммутатор учреждения обслуживает 200 абонентов. Вероятность того, что в течение одной минуты абонент позвонит на коммутатор, равна 0,01. Найти вероятность того, что в течение минуты позвонят более двух абонентов.
8. В команде 9 спортсменов, из них 4 первого разряда и 5 второго. Наудачу выбраны 4 спортсмена. Найти ряд распределения дискретной случайной величины X —числа спортсменов второго разряда среди отобранных. Построить многоугольник распределения, вычислить математическое ожидание M(X) и среднее квадратическое отклонение (X) этого ряда и отобразить их на многоугольнике распределения.
9. Плотность вероятностей случайной величины Х равна
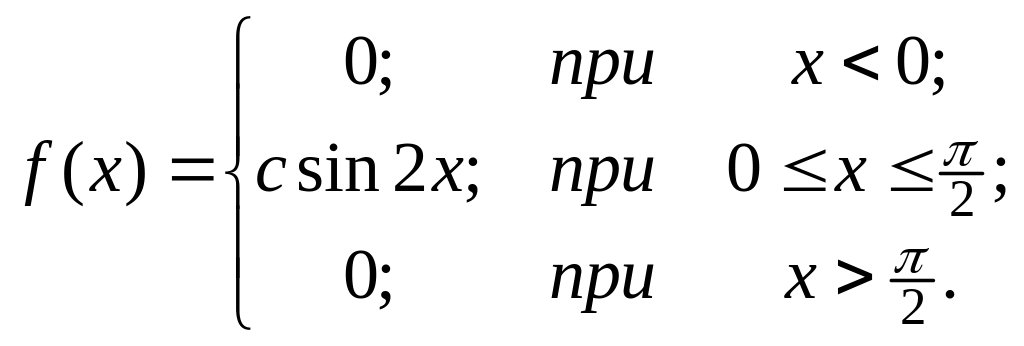
Найти коэффициент c, интегральную функцию распределения F(x), математическое ожидание M(X), среднее квадратическое отклонение (X) и вероятность P(0,5<X<1). Построить графики плотности и функции распределения и на показать них математическое ожидание и среднее квадратическое отклонение (X).
10. На станке изготавливается деталь. Ее длина X —случайная величина, распределенная по нормальному закону с параметрами a = 23,0 см,
= 0,6 см. Найти вероятность того, что длина детали будет заключена между 22,1 и 23,9 см. Какое отклонение длины детали от a можно гарантировать с вероятностью 0,92; 0,98? В каких пределах, симметричных относительно a, будут лежать практически все размеры деталей?
11. На основе данных о результатах 49‑ти измерений времени предварительного застывания цементного раствора марки 300 (30% твердости)
No |
t[час] |
No |
t[час] |
No |
t[час] |
No |
t[час] |
No |
t[час] |
1 |
11,2 |
11 |
14,6 |
21 |
15,8 |
31 |
16,6 |
41 |
18,0 |
2 |
11,6 |
12 |
14,8 |
22 |
15,8 |
32 |
16,7 |
42 |
18,2 |
3 |
12,0 |
13 |
15,1 |
23 |
15,9 |
33 |
16,7 |
43 |
18,4 |
4 |
12,5 |
14 |
15,2 |
24 |
16,0 |
34 |
16,8 |
44 |
18,6 |
5 |
13,1 |
15 |
15,3 |
25 |
16,1 |
35 |
16,8 |
45 |
18,8 |
6 |
13,4 |
16 |
15,4 |
26 |
16,2 |
36 |
16,9 |
46 |
19,4 |
7 |
13,6 |
17 |
15,5 |
27 |
16,3 |
37 |
17,2 |
47 |
19,8 |
8 |
13,9 |
18 |
15,6 |
28 |
16,4 |
38 |
17,5 |
48 |
20,2 |
9 |
14,1 |
19 |
15,6 |
29 |
16,5 |
39 |
17,6 |
49 |
20,6 |
10 |
14,4 |
20 |
15,7 |
30 |
16,5 |
40 |
17,8 |
|
|
сформировать таблицу значений относительных частот для равноотстоящих вариант, таблицу значений эмпирической плотности относительных частот и эмпирической функции распределения, разбив рассматриваемый отрезок значений исследуемого параметра на 7 равноотстоящих частичных интервалов.
12. Построить полигон и гистограмму относительных частот и график эмпирической функции распределения.
13. Вычислить выборочную среднюю выборки, её дисперсию, выборочное среднее квадратическое отклонение и выборочные коэффициенты асимметрии и эксцесса, отобразив выборочную среднюю и выборочное среднее квадратическое отклонение на полигоне и гистограмме относительных частот.
14. Найти точечные оценки параметров нормального закона распределения, записать соответствующую формулу для плотности вероятностей f(x) и рассчитать теоретические относительные частоты. Построить график плотности распределения на гистограмме относительных частот, а теоретические относительные частоты показать на полигоне относительных частот.
15. Найти интервальные оценки параметров нормального закона распределения, приняв доверительную вероятность = 0,95 и 0,99.
16. Проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности с эмпирическим распределением выборки, используя критерий Пирсона при уровнях значимости 0,01; 0,05.
17. Найти выборочное уравнение линейной регрессии признака Y на признаке X и коэффициент их корреляции по экспериментальным данным из таблицы
-
nij
X
10
20
30
40
50
60
Y
30
5
10
40
15
5
50
20
80
60
5
10
35
70
5
10