1. Зависимость от концентрации фермента

По уравнению

Скорость реакции при определенной концентрации субстрата должна линейно зависеть от концентрации фермента. Для большинства ферментативных реакций это не соответствует действительности. Нужно учитывать, что уравнение приводится для концентрации субстрата, которая значительно превосходит концентрацию фермента. Линейная зависимость будет выполняться, пока будут соблюдаться эти условия. В случае значительного повышения концентрации [E₀] имеет место отклонение от линейности, а при некоорых концентрациях (E) скорость реакции повышаться не будет. Это связано с тем, что концентрация комплекса (ES) – промежуточного продукта реакции не будет повышаться в случае отсутствия достаточного количества свободного субстрата.

В некоторых случаях, даже при соблюдении условий, когда , линейная зависимость между v и [E₀] не наблюдается, что может свидетельствовать о более сложном механизме ферментативной реакции, по сравнению с тем, который описывается химическим уравнением (1.1) и о невозможности применения уравнения Михаэлиса–Ментен.

2. Зависимость скорости реакции от концентрации субстрата.

Зависимость скорости ферментативной реакции от концентрации субстрата при постоянной концентрации фермента определяется гиперболичной функцией:

V

V_max

K_m S

2.1. В случае незначительных концентраций субстрата, когда , можно принять, что, , тогда .

Скорость реакции линейно зависит от концентрации субстрата.

2.2. При , , т.е. скорость реакции не зависит от концентрации субстрата и равна максимальной скорости реакции.

Определение параметров V_m и K_m из экспериментальных данных

Как правило, из данных по стационарной кинетике величины V_m и K_m определяют на основе линеаризации уравнения Михаэлиса–Ментен.

1. Метод двойных обратных координат (Метод Лайнуивера–Берка)

2 . Метод Хейнса

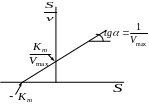
3 . Метод Скэтчарда (Иди–Хофсти)

Ингибирование ферментов

Исследование кинетики действия ферментов является основой для установления характера действия многих ингибиторов. Ингибиторы можно разделить на две группы –обратимые и необратимые. При действии обратимого ингибитора после его удаления (с помощью диализа) активность фермента восстанавливается (при действии необратимого ингибитора- не восстанавливается). Необратимое ингибирование является прогрессирующим и становится полным в том случае, если весь фермент оказывается связанным с ингибитором, в то время как обратимое ингибирование достигает состояния равновесия, определяемое ингибиторной константой, то есть константой диссоциации комплекса фермент- ингибитор.

Различают три типа обратимого ингибирования, а именно: конкурентное, неконкурентное и бесконкурентное. При конкурентном и неконкурентном ингибировании наблюдается изменение кажущихся величин и соответственно.

Конкурентный ингибитор- это соединение, которое благодаря большому структурному сходству с истинным субстратом, способно взаимодействовать с активным центром и, следовательно, конкурировать с субстратом за фермент; он увеличивает . Скорость реакции снижается, поскольку комплекс фермент- ингибитор является неактивным, то есть не распадается с образованием продуктов. Степень ингибирования зависит от относительных концентраций субстрата и ингибитора, и при достаточно большой концентрации субстрата ингибирование может быть полностью подавлено.

При неконкурентном ингибировании степень обратимого ингибирования зависит только от концентрации ингибитора и не изменяется при варьировании концентрации субстрата. Это свидетельствует о том, что взаимодействие ингибитора с ферментом происходит на участке, важном для активности, но не в самом активном центре, где связывается субстрат, то есть сродство фермента к своему субстрату не изменяется; ингибитор влияет на .

Бесконкурентное ингибирование наблюдается в том случае, когда ингибитор не взаимодействует со свободным ферментом, а способен связываться только с комплексом фермент- субстрат или другими формами фермента, которые не присоединяют субстрат. Поэтому представляется вероятным, что в том случае, когда образование комплекса с субстратом не изменяет конформацию фермента, взаимодействие комплекса с ингибитором должно осуществляться, по крайней мере частично, при участии связанного субстрата. Бесконкурентное ингибирование влияет как на связывание субстрата так и на максимальную скорость, и, как будет показано ниже, характерной чертой для бесконкурентного ингибирования является уменьшение и в одно и то же число раз.

Следует подчеркнуть, что тип ингибирования, наблюдаемый при действии данного соединения, зависит от природы фермента. Например, соединение может действовать как конкурентный ингибитор по отношению к одному ферменту и как неконкурентный– по отношению к другому.

Установление типа ингибирования (конкурентного, неконкурентного и бесконкурентного) может быть осуществлено экспериментально; при этом используют кинетические уравнения ингибирования.