1.2. Кинетика ферментативных реакций Механизм действия ферментов

Около 50% белков являются ферментами и могут ускорять ту или иную реакцию. Ускорение достигается за счет улучшения кинетических характеристик реакции.

Рассмотрим, за счет чего, в принципе, может осуществляться этот эффект.

1. Способы ускорения реакций.

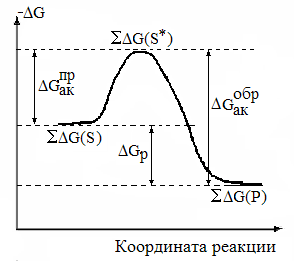
Обратимся, для определенности к двусубстратной реакции вида: (1) и ее энергетической диаграмме (рис.1.2.1). На диаграмме: 1. и - соответственно, общая средняя энергия субстратов (АВ и С) и продуктов (А, ВС); 2. их разница - , энер­гия реакции; 3. – энергетический барьер, или энергия то­го возбужденного состояния субстратов, в котором они и мо­гут вступать в реакцию; 4. разница между средней энергией и энергетическим барьером - энергия активации прямой или обратной реакции, если

Рис.1.2.1. Энергетическая диаграмма реакции вида

речь идёт о средней энергии, соответственно, субстратов или продуктов:

Обе эти величины всегда положительны. Из диаграммы ясна также связь между энергией активации прямой и обратной реакций:

Для скорости прямого превращения справедливы формулы:

(1) (2)

где формула (2) – уравнение Эйринга, Отсюда ясно, что скорость реакции определяется лишь следующими параметрами (не считая температуры) – концентрациями участников ( ) и энергией активации реакции ( ).

Это означает, что катализатор любой природы (в т.ч. и фермент) имеет всего три принципиальные возможности ускорить реакцию:

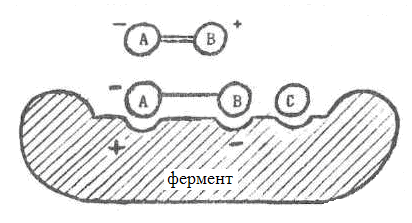
I. увеличить эффективную концентрацию участников. Увеличение эффективной концентрации достигается за счет того, что фермент имеет центры связывания для обоих субстратов, так что при связывании с ними молекулы субстратов во-первых, сильно сближаются, а во-вторых, правильно ориентируются друг относительно друга.

II. Уменьшить энергию активации

А. "снизу", за счет увеличения энергии субстратов .

Суть данного феномена в том, что взаимодействие субстрата с ферментом ведет к созданию в молекуле субстрата напряженной конформации (такой, в которой субстрат легче вступает в реакцию).

Например, как показано на рис.1.2.2, расстояние на ферменте между центрами связывания групп А и В субстрата АВ несколько больше длины молекулы АВ. Поэтому при связывании связь А—В как бы "растягивается", что и означает переход субстрата в возбужденное состояние. Таким образом, здесь имеет место передача некоторого количества энергии от фермента к субстрату. Но потом, когда фермент переходит в начальное состояние, эта энергия ему возвращается за счет выделяющейся энергии реакции.

Рис. 1.2.2. Механизм снижения энергии активации за счет увеличения энергии субстратов.

Б. либо "сверху", за счёт снижения энергетического барьера .

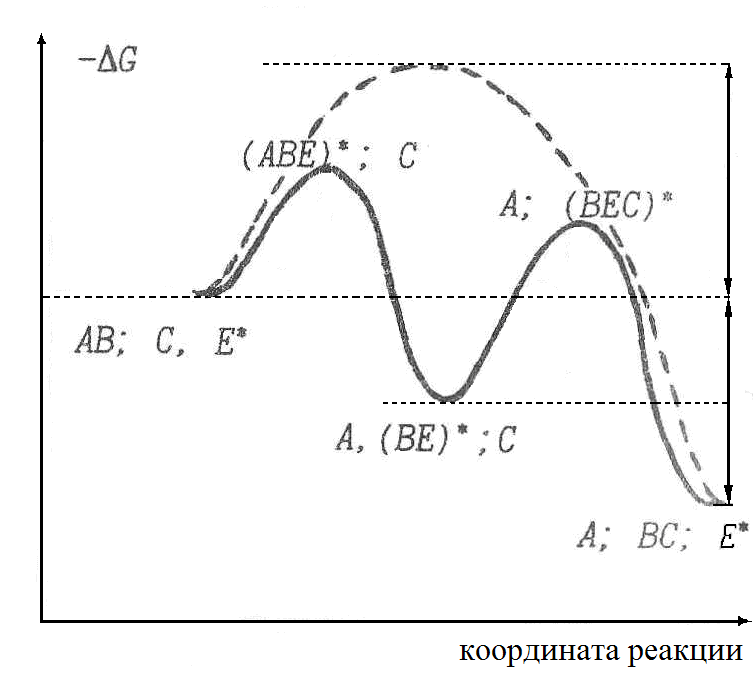
Энергетический барьер обычно снижается путем разбиения исходной реакции на несколько других, причем таких, что энергия активации в каждой из них оказывается меньше, чем в исходной (1.2.3).

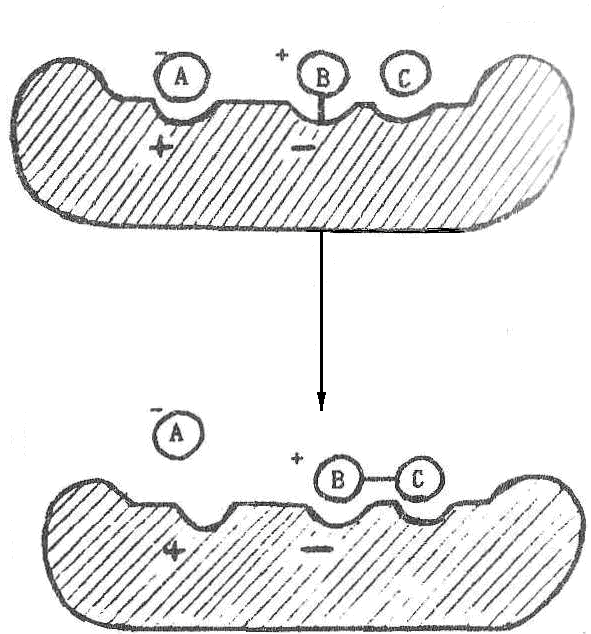
Например, пусть после разрыва связи А—В группа В предварительно образует связь с ферментом (ковалентную или иную) (1.2.3), т.е. вместо реакции (1) получаются реакции:

И пусть соответствующая группа фермента, участвующая в образовании связи, находится в возбужденном состоянии (за счет влияния окружающих радикалов).

Тогда энергия активации каждой из промежуточных реакций (рис. 1.2.3) окажется меньше, чем для исходной реакции. В каждой из них энергия требуется для активации только одного из двух участников реакции: в первой - только для АВ, а во второй - только для С. Скорость результирующего процесса будет определяться той из двух промежуточных реакций, у которой энергия активации больше.

Рис. 1.2.3. Механизм снижения энергии активации за счет снижения энергетического барьера.

Все эти три возможности используются в катализе (как ферментативном, так и неферментативном), причем одни катализаторы реализуют сразу две-три из них, а другие - лишь какую-либо одну.