Влияние температуры на скорость химической реакции

Скорость протекания любой химической реакции зависит от условий проведения эксперимента: состава реакционной смеси, температуры, давления, рН и т.д.

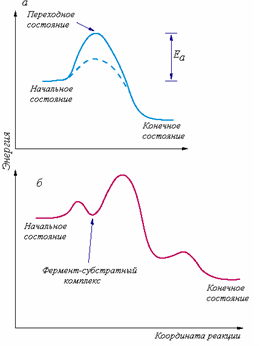
Рис.1.1.3. Схематическое представление изменения свободной энергии в ходе реакции: а– пунктирная линия – снижение барьера свободной энергии; б–фермент разбивает высокий барьер на несколько более мелких.

Модификация условий эксперимента может привести к изменению величины константы скорости реакции или к трансформации механизма протекания реакции. Зависимость константы скорости реакции от температуры описывается уравнением Аррениуса: Зависимость данного типа в 1889 году впервые получил С.Аррениус. Большую роль сыграла опубликованная пятью годами раньше книга Я. Вант-Гоффа «Очерки по химической динамике», в которой он эмпирическим путем вывел уравнение для температурной зависимости константы равновесия реакции (уравнение изохоры Вант-Гоффа). Для объяснения полученной зависимости Аррениус исходил примерно из следующих соображений. Скорость реакции пропорциональна числу столкновений молекул реагирующих веществ. Поэтому разумно предположить, что константа скорости также пропорциональна этому числу столкновений. Следовательно,

где Р-коэффициент пропорциональности (фактор аддиабативности); Z- число столкновений между молекулами.

Если бы любое столкновение между молекулами приводило к образованию продуктов химической реакции, то температура не оказывала бы столь большое влияние на скорость протекания химической реакции. Следовательно, химическая реакция протекает в результате столкновения не любых, а только «активных» молекул. Число таких молекул должно возрастать при увеличении температуры.

Согласно предположениям Аррениуса, разница между «активной» и «неактивной» молекулами определяется энергией молекулы. Для каждой химической реакции существует своя критическая величина E, называемая энергией активации. Как только энергия молекулы больше, чем Е, она «активна».

Энергией активации называется количество энергии, которая необходима для переведения одного моля вещества в активированное состояние при определенной температуре. Ее определяют опытным путем, обозначают буквой E (Е_a) и обычно выражают в кДж/моль.

Графически эта величина соответствует величине барьера (образование переходного состояния, рис. 1.1.3), который необходимо преодолеть для осуществления химической реакции (соответствует разности энергий Гиббса переходного и исходного состояний).

Реакция возможна, если она идет с понижением энергии. Это необходимое, но не достаточное условие.

Еще до Аррениуса было показано, что доля молекул с энергией больше, чем Е, равна, где R—универсальная газовая постоянная. Поэтому разумно предположить, что . Тогда:

Обозначая предэкспоненциальный множитель как , получаем современный вид уравнения Аррениуса:

Строим графическую зависимость в координатах — (рис. 1.1.4).

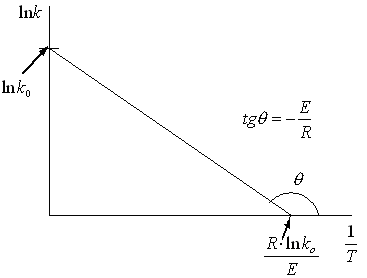
Рис.1.1.4. Определение энергии активации исходя из температурной зависимости.

Д ифференцируем последнее уравнение по Т:
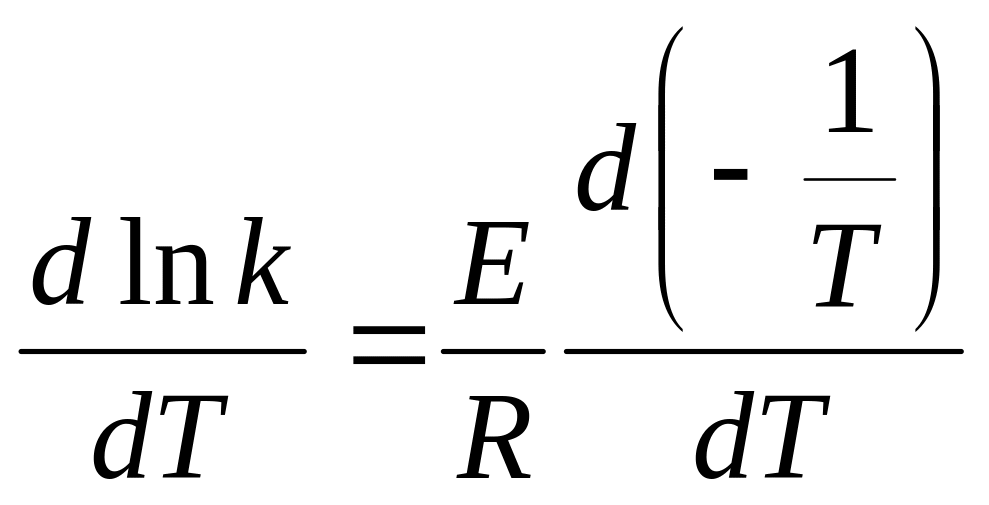
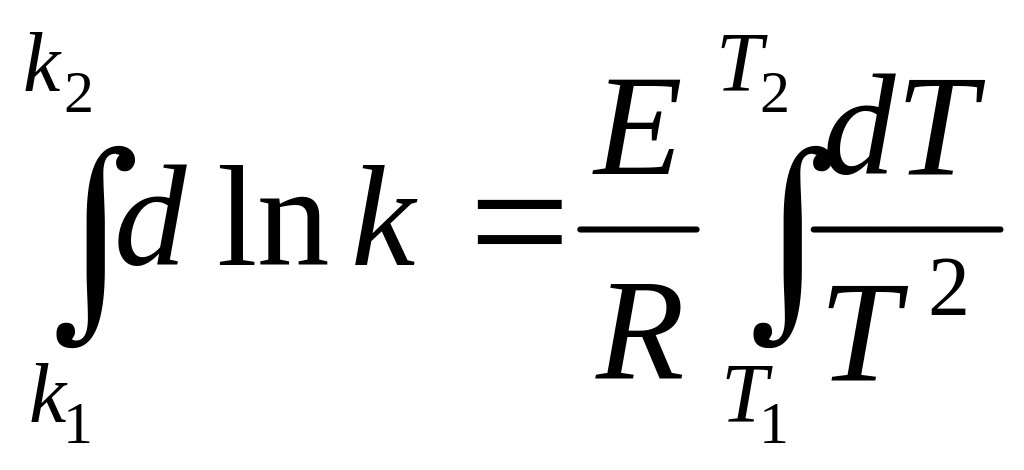