
- •Раздел I. Кинетика ферментативных процессов
- •1.1. Формальная кинетика
- •Закон действующих масс
- •Константа скорости реакции
- •Порядок химической реакции
- •Обратимые химические реакции
- •Влияние температуры на скорость химической реакции
- •Кинетика реакций Реакции первого порядка
- •Кинетическое уравнение реакции второго порядка
- •Метод Гуггенгейма
- •1.2. Кинетика ферментативных реакций Механизм действия ферментов
- •II. Уменьшить энергию активации
- •Уравнение Михаэлиса-Ментен
- •1. Зависимость от концентрации фермента
- •2. Зависимость скорости реакции от концентрации субстрата.
- •2 . Метод Хейнса
- •3 . Метод Скэтчарда (Иди–Хофсти)
- •Ингибирование ферментов
- •Конкурентное ингибирование
- •Графическое определение параметров конкурентного ингибирования
- •Бесконкурентное ингибирование
- •Графические методы определения параметров бесконкурентного ингибирования
- •1. Лайнуивера-Берка
- •2 . Хейнса
- •4. График Диксона
- •Неконкурентное ингибирование
- •1. Метод Лайнуивера-Берка
- •4. График Диксона
- •1. Общие сведения.
- •2. Ввод данных.
- •3. Построение графика.
- •4. Определение параметров поставленной задачи.
- •Лабораторная работа № 2. Определение кинетических параметров ферментативной реакции.
- •Задание для самостоятельной подготовки
- •Задание к работе.
- •Задания к лабораторной работе 2 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10.
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Р аздел іі. Изучение динамических моделей биологическихпроцессов Общие принципы описания кинетического поведения биологических систем
- •Качественное исследование простейших моделей биологических процессов
- •Простейшие математические модели
- •1. Модель экспоненциального роста популяций
- •Решение представляет собой формулу экспоненциального роста
- •2. Модель сезонного роста
- •3. Модель логистического роста
- •Качественные методы исследования систем дифференциальных уравнений
- •Устойчивость стационарного состояния. Фазовые портреты
- •Модели биологических процессов, описываемые системой дифференциальных уравнений
- •1. Виды конкурируют за одну и ту же пищу, запасы которой ограничены
- •2. Модель логистического роста (модель плотностного давления)
- •3. Модель хищник – жертва Вольтерра
- •4. Биологический метод борьбы с нежелательным видом. Метод Кюрасао.
- •Мы изучаем наиболее простую модель, предложенную Базыкиным.
- •Возможности MathCad, которые можно использовать при изучении темы
- •1. Символьное решение определителя матрицы для нахождения корней характеристического уравнения
- •2. Нахождение частных производных с помощью программы MathCad
- •3. Символьное решение уравнений и систем уравнений
- •Лабораторная работа 1 Численные методы решения дифференциальных уравнений и систем дифференциальных уравнений
- •I. Изменение численности популяции описывается одним дифференциальным уравнением
- •Задание 1
- •Задание 2
- •Изменение численности популяции описывается системой уравнений. Один вид ведет себя по отношению к другому как хищник Задание 3
- •Задание 4
- •Лабораторная работа № 2 Математические модели распространения инфекционных заболеваний Модель 1
- •Модель 2.
- •Модели эпидемий с переносчиками
- •Раздел ііі. Термодинамика биологических процессов обзор по равновесной термодинамике
- •1. Первый и второй законы термодинамики
- •Второй закон термодинамики
- •Энтропия и вероятность состояния
- •2. Характеристические функции
- •Для равновесных процессов:
- •Для неравновесных процессов:
- •Самопроизвольные процессы при постоянных t и p
- •Полезная работа и приращение свободной энергии
- •Выражение для свободной энергии в явном виде
- •Стандартные состояния. Стандартные условия
- •Химический потенциал
- •Электрохимический потенциал
- •Расчеты стандартных энергий биохимических реакций
- •Описание систем в термодинамике неравновесных процессов
- •1. Второй закон термодинамики в открытых системах
- •Особенности открытых систем
- •Возрастание энтропии вследствие необратимых процессов внутри открытых систем
- •Диссипация энергии в скалярных необратимых процессах
- •Диссипация энергии в векторных необратимых процессах
- •Диссипация свободной энергии в сопряженных скалярных и векторных процессах
- •Соотношения между значениями движущих сил и скоростей процессов. Соотношения Онзагера
- •Примеры линейных соотношений
- •– Соответствуют возможной взаимосвязи двух потоков и носят название коэффициентов взаимности Онзагера.
- •Пример:
- •Теорема Пригожина.
- •Список рекомендованной литературы Основная литература
- •Дополнительная литература
Качественные методы исследования систем дифференциальных уравнений
Качественные методы исследования подобных систем рассмотрим на моделях, представимых в виде систем двух автономных дифференциальных уравнений:
![]()
![]()
Здесь
![]() ,
,
![]() - непрерывные функции, определенные в
некоторой евклидовой плоскости (x,y
– декартовы координаты) и имеющие в
этой области непрерывные производные
порядка не ниже первого.
- непрерывные функции, определенные в
некоторой евклидовой плоскости (x,y
– декартовы координаты) и имеющие в
этой области непрерывные производные
порядка не ниже первого.
Область
может быть как неограниченной, так и
ограниченной. В том случае, когда
переменные величины
![]() имеют конкретный биологический смысл,
на них накладываются некоторые
ограничения. Прежде всего, биологические
переменные не могут быть отрицательными.
Так, в модели Вольтерра,
имеют конкретный биологический смысл,
на них накладываются некоторые
ограничения. Прежде всего, биологические
переменные не могут быть отрицательными.
Так, в модели Вольтерра,
![]() - переменная, характеризующая численность
жертвы, а
- переменная, характеризующая численность
жертвы, а
![]() - хищника. Область
- хищника. Область![]() представляет собой положительный
квадрат правой полуплоскости:
представляет собой положительный
квадрат правой полуплоскости:
![]()
В
процессе изменения состояния системы
во времени переменные
изменяются согласно системе уравнений,
так что каждому состоянию системы
соответствует пара значений
.
Рассмотрим плоскость с осями координат,
на которых отложены значения переменных
![]() Такая плоскость носит название фазовой
плоскости.
Она представляет совокупность всех
возможных состояний системы.
Такая плоскость носит название фазовой
плоскости.
Она представляет совокупность всех
возможных состояний системы.
Точка
![]() называется изображающей.
Пусть, при
называется изображающей.
Пусть, при
![]() ,
координаты изображающей точки
,
координаты изображающей точки
![]() .
В каждый следующий момент времени
.
В каждый следующий момент времени
![]() изображающая точка будет двигаться в
соответствии с системой уравнений и
принимать положение
,
соответствующее значениям
,
изображающая точка будет двигаться в
соответствии с системой уравнений и
принимать положение
,
соответствующее значениям
,
![]() .
.
Совокупность этих точек на фазовой плоскости называется фазовой траекторией. Характер фазовых траекторий отражает общие качественные черты поведения системы во времени.
Изображающая
точка с координатами
![]() ,
называется стационарной,
и в этой точке
,
называется стационарной,
и в этой точке
![]()
Устойчивость стационарного состояния. Фазовые портреты
1. Стационарная точка типа узел.
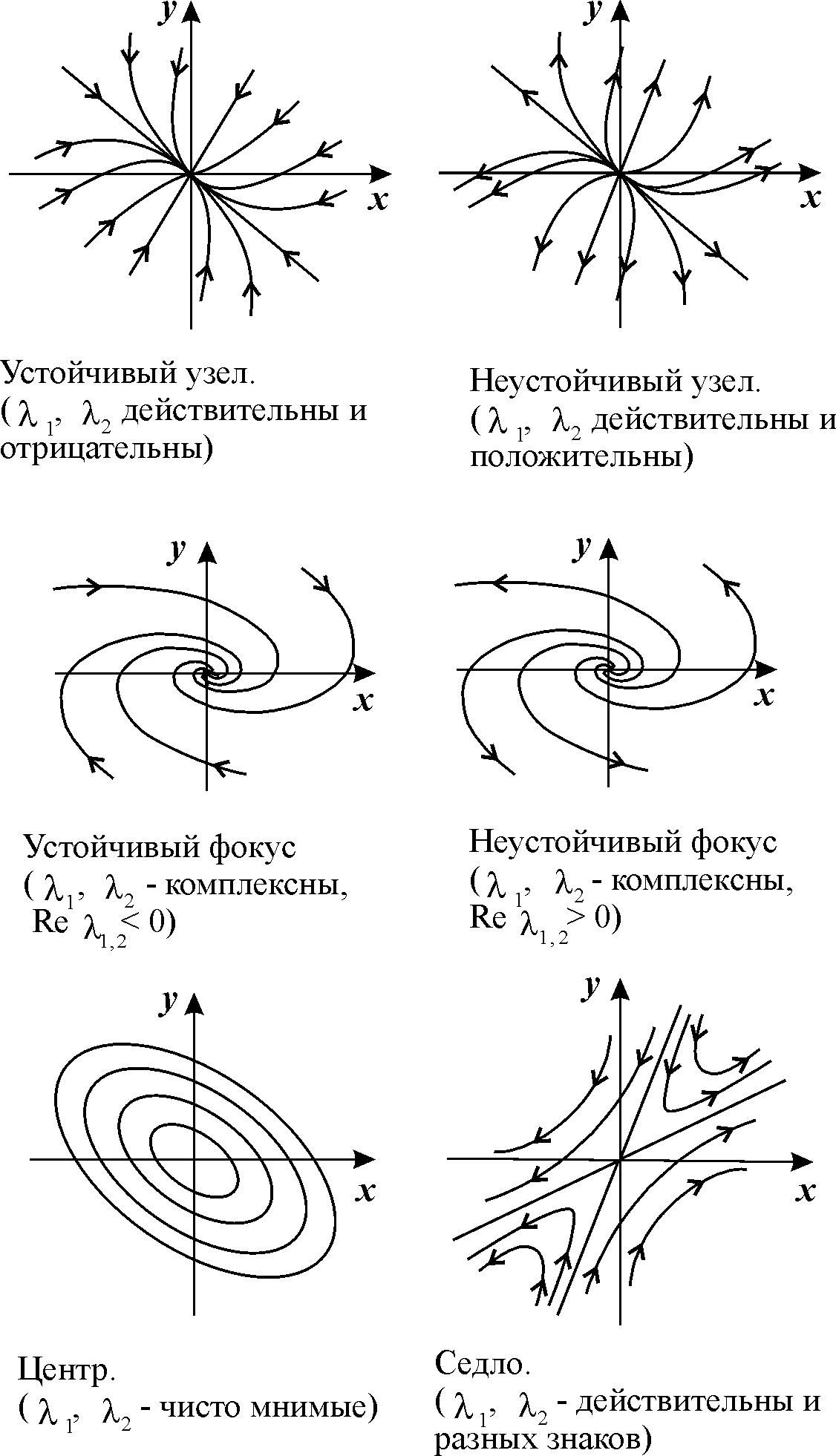
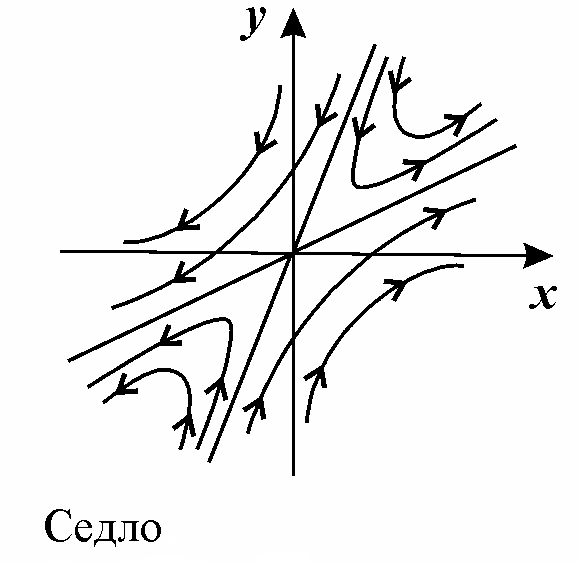
2. Поведение переменных изображается на фазовой плоскости кривыми гиперболического типа. Такая особая точка является неустойчивой и называется особой точкой типа “седло”. Легко видеть, где бы ни находилась изображающая точка в начальный момент, она всегда в конечном счете будет удаляться от равновесия.
3. Изменение переменных во времени носит колебательный характер, а фазовая траектория представляет собой спирали. Особая точка в этом случае называется фокусом. При этом, если колебания затухают, то положение равновесия является устойчивым фокусом, если амплитуда колебаний со временем нарастает, то особая точка является неустойчивым фокусом.
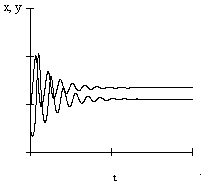
Затухающие колебания
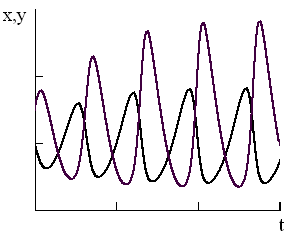
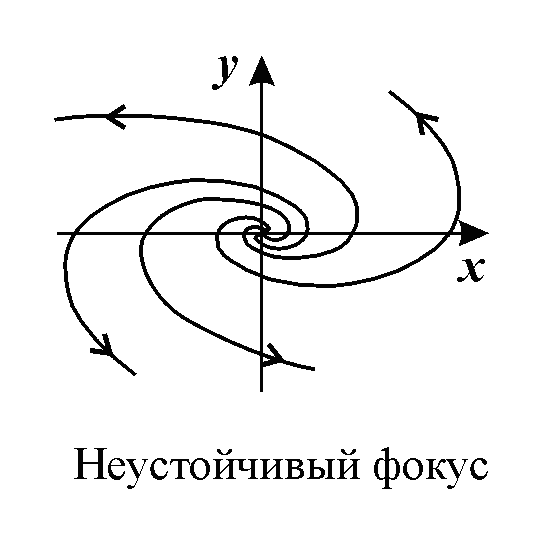
 Наростающие
колебания
Наростающие
колебания
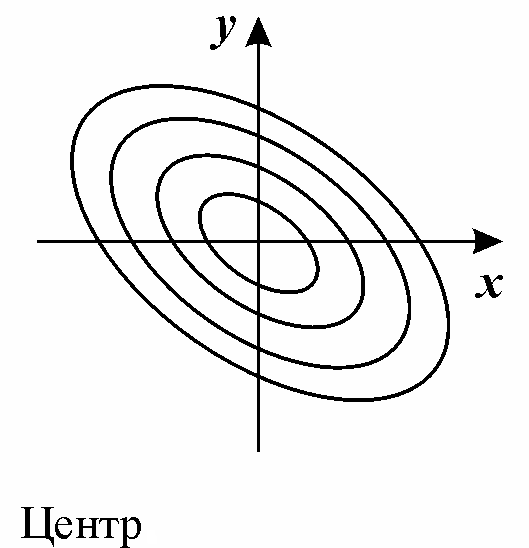
4. В том случае, когда фазовые траектории в окрестности особой точки представляют собой эллипсы, через особую точку не проходит ни одна интегральная кривая.
Такая изолированная особая точка, вблизи которой фазовые траектории представляют замкнутые кривые (эллипсы), “вложенные друг в друга” и охватывающие особую точку, называется центром.
Классическим примером системы, имеющей своей особой точкой центр, является система уравнений Вольтерра.
