Вариант 6

Метионин образуется при биосинтезе (Escherichia coli) в результате ферментативного метиллрования гомоцистеина 5-метилтетрагидроптероилтриглутаматом. Образование метионина регистрировали микробиологическим методом. Были получены следующие результаты:

Триглутамат, мкмоль/л	Кол-во образовавшегося метионина, нмоль
10	500
12,5	526
16,7	555
25	589
50	714

Найти константу Михаэлиса и максимальную скорость реакции методами Лайнуивера-Бэрка, Эди-Хофсти и Хейнса. Сравните полученные результаты.

Вариант 7

При изучении зависимости скорости реакции от концентрации субстрата были получены след. данные. Субстратом служил фенолфталеинглюкуронид; скорость реакции выражали в микрограммах фенолфталеина, освобождаемого за 60 минут при 37^оС. Найти константу Михаэлиса и максимальную скорость реакции методами Лайнуивера-Бэрка, Эди-Хофсти и Хейнса. Сравните полученные результаты.

Концентрация субстрата, мМ	Скорость реакции
1	32
2	43,6
3	50,4
4	53
5	56,5
10	62,1

Вариант 8

Начальная скорость окисления сукцината натрия в фумарат натрия под действием фермента сукциноксидазы была измерена для ряда концентраций субстрата:

[S], моль/л	0,01	0,002	0,001	0,0005	0,00033
V·106, моль/(л·с)	1,17	0,99	0,79	0,62	0,50

Определите константу Михаэлиса и максимальную скорость данной реакции методами Лайнуивера-Бэрка, Эди-Хофсти и Хейнса. Сравните полученные результаты

Вариант 9

Н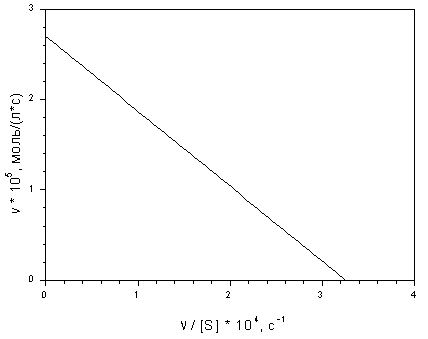 айдите константу Михаэлиса и максимальную скорость каталитического разложения гидроперекиси тетралина по следующим кинетическим данным:

Используя уравнение Михаэлиса-Ментен, найдите значения концентрации субстрата для нескольких значений скорости реакции. По полученным данным рассчитайте максимальную скорость реакции и константу Михаэлиса методами Лайнуивера-Бэрка и Хейнса. Сравните полученные результаты.

П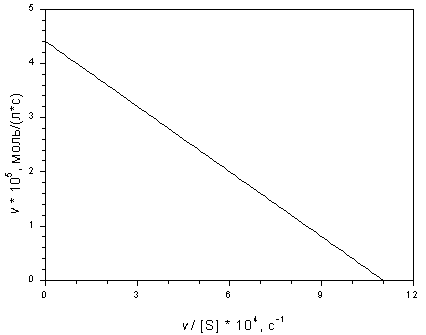 римечание: Для нахождения концентраций субстрата выбрать несколько значений скорости по предложенному графику и записать их в виде массива. Из уравнения Михаэлиса-Ментен выразить значение S через найденные величины V, K_m и V_max. Поскольку полученная формула предполагает действия с векторами, над выражением необходимо поставить знак вектора (панель инструментов Matrix, кнопка с изображением ).

Вариант 10.

Найдите константу Михаэлиса и максимальную скорость каталитического окисления циклогексена трет-бутилпероксидом по следующим кинетическим данным:

Используя уравнение Михаэлиса-Ментен, найдите значения концентрации субстрата для нескольких значений скорости реакции. По полученным данным рассчитайте максимальную скорость реакции и константу Михаэлиса методами Лайнуивера-Бэрка и Хейнса. Сравните полученные результаты.

Лабораторная работа № 3.

Влияние ингибиторов на кинетику ферментативных реакций.

Задание для самостоятельной подготовки:

1. Знать типы ингибирования и соответствующие им уравнения скорости ферментативной реакции.

2. Уметь по графику в координатах Лайнуивера-Бэрка, Эди-Хофсти, Хейнса и Диксона определять тип ингибирования, константу ингибирования, кинетические параметры ферментативной системы.

Задание к работе.

Определить тип ингибирования и константу диссоциации комплекса фермент  ингибитор, исходя из данных таблицы.

1. Построить точечные графики в координатах Лайнуивера-Бэрка. На одной координатной плоскости расположить графики без и в присутствии ингибитора.

2. С помощью функций slope и intercept определить тангенсы угла наклона полученных прямых и отрезки, отсекаемые на оси ординат.

3. На графике Лайнуивера-Бэрка пострить прямые, проходящие через точки, и для определения типа ингибирования полученные прямые продлить до точки их пересечения, как это описано в Лабораторной работе 2.

4. По виду полученных графиков определите тип ингибирования.

5. По тангенсам угла наклона и отрезкам, отсекаемым на осях найти константу Михаэлиса, максимальную скорость реакции, константу диссоциации фермент-ингибиторного комплекса.

6. Построить графики и найти кинетические параметры методами Эди-Хофсти, Хейнса и Диксона. Сравнить полученные результаты.

Примечание.

При нахождении кинетических параметров методом Диксона выполнить следующую последовательность действий:

- ввести вектор значений концентраций ингибитора;

- массивы для скоростей реакции сформировать следующим образом: каждому массиву задается новое имя (например, Vd1, Vd2 …); количество массивов равно числу концентраций субстрата; количество элементов в массиве соответствует количеству концентраций ингибитора. Элементами каждого массива являются значения скоростей реакции для выбранной концентрации субстрата при всех концентрациях ингибитора.

При нахождении константы ингибирования по методу Диксона для решения системы уравнений используется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:

• Given — ключевое слово;

• система уравнений, записанная в виде равенств.

• Find(x₁... ,х_n) — встроенная функция для решения системы относительно переменных х₁, ...x_n.

Блок Given/Find использует для поиска решения итерационные методы, поэтому перед ключевым словом Given требуется задать начальные значения для всех х. Значение функции Find есть вектор, составленный из решения каждой переменной. Таким образом, число элементов вектора равно числу аргументов Find.

Например, необходимо найти решение системы уравнений:

В программе MathCad запись решения системы будет выглядеть следующим образом:

Присваиваем начальные значения переменным х и y:

Вводим операторы блока Given/Find и систему уравнений:

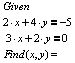
Знак равенства [ ] в системе уравнений вводится с помощью комбинации клавиш [Ctrl]+[=]; знак равенства после оператора Find служит для вывода результата на экран и вводится с клавиатуры нажатием обычного символа [=].