5 (Пунктирная линия),
10 (Штрих - пунктирная линия),
15 (Штриховая линия).
На рис. 2.6 построены
ПРВ при заданных параметрах, полученные
аналитически при количествах членов
ряда
5
(пунктирная линия), 10 (штрих - пунктирная
линия) и 15 (штриховая линия), а также
моделированием (сплошная линия). В данном
случае получается аналогичный результат,
т.е. при оптимальном количестве членов
ряда Фурье
расчётные значения заметно отличаются
от значений, полученных с помощью модели,
хотя оценки расстройки по частоте
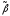близки.
2.3. Анализ срыва слежения.
Одной из важнейших
характеристик системы является её
устойчивость во времени, т.е. способность
осуществлять слежение без срывов в
течение заданного промежутка времени
[14]. Под срывом будет понимать момент
времени, когда рассогласование по фазе
достигает величины
.
Рис. 2.7. Зависимость
рассогласования
от времени при
.
На рис. 2.7 представлена
зависимость
,
которая иллюстрирует типовой процесс
срывов слежения при значении
.
В момент срыва
изменяется на
.
2.3.1. Расчёт среднего времени до срыва слежения.
В общем случае
среднее время до срыва синхронизации
находится из решения уравнения Понтрягина
[10, 11]. Существует приближённая формула
для расчёта времени до срыва, которая
справедлива при малых
и больших значениях
и имеет вид
.
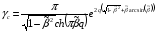(2.5)
Произведём
моделирование срыва и сравним результаты.
Для обработки результатов моделирования
можно воспользоваться следующим методом.
Модель необходимо перестроить так,
чтобы при достижении границы
система автоматически сбрасывалась в
и продолжала работу из этого состояния,
при этом данные
со счётчика реального времени поступают
на хранение, затем счётчик сбрасывается
и начинает считать дальше. Таким образом,
по окончании моделирования в памяти
будет набор случайных времён сброса
,
где
,
а
получается автоматически. Соответственно
среднее время до срыва слежения равно
.
На рис. 2.8 представлена
зависимость среднего времени до срыва
слежения
от ОСШ
при
0,
0.2 и 0.5, полученная расчётом (штриховая
линия) и моделированием (сплошная линия).
Рис. 2.8. Зависимость
от
при
0,
0.2 и 0.5, полученная
расчётом (штриховая линия) и
моделированием (сплошная линия).
Из графика на рис.
2.8 можно сделать вывод, что аналитическое
выражение (2.5) можно использовать при
расчёте
,
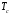однако необходимо сделать поправку
коэффициента
в экспоненте. Причём исходные зависимости
дают точный результат при малых
и больших
.
2.3.2. Расчёт вероятности срыва слежения.
Вероятность
достижения границ интервала
определяется как
,
где
- вероятность того, что границы не
достигаются. Вероятность
удовлетворяет неравенству
,
(2.6)
при этом
является решением уравнения
,
а оператор
,
в котором
[11]. В итоге получается система уравнений,
которая решается численными методами.
Существует приближённая формула для
расчёта вероятности срыва
,
в которой
можно принять равной
[11].
Для нахождения
по результатам моделирования можно
воспользоваться уже полученными ранее
значениями
.
Для этого сначала найдём
при
.
Затем зафиксируем дискретный момент
времени
и проанализируем все
при
,
чтобы найти количество элементов, для
которых выполняется неравенство
.
Всего таких элементов будет
,
тогда вероятность срыва в момент
равна
.
Получена
- вероятность срыва в один момент
времени, всего таких времён будет
,
потому что при
срыв будет всегда, тогда
.
На рис. 9 представлена
зависимость
,
полученная аналитически (штриховая
линия) и моделированием (сплошная линия)
при
и значениях ОСШ
0.25,
0.5, 1, 2, 4.
Рис. 2.9. Зависимость
при
и
0.25,
0.5, 1, 2, 4, полученная
аналитически (штриховая линия) и
моделированием (сплошная линия).
Из графика на рис.
2.9 видно, что семейство кривых достаточно
точно может быть описано зависимостью
,
однако
требует коррекции, потому что при
кривые при
повторяют друг друга, но при других
,
особенно больших, они сильно расходятся.
Проведём аналогичные
рассуждения для случая, когда
.
Аналитический
расчёт вероятности срыва при
представляет собой трудоёмкую задачу,
поэтому на рис. 10 представлена зависимость
,
полученная моделированием при
и значениях ОСШ
2
(сплошная линия), 4 (штриховая линия) и 8
(штрих - пунктирная линия).
Рис. 2.10. Зависимость
при
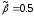и значениях