5.3. Модель с одной петлёй.

В предыдущем разделе была изложена идея добавления к входному сигналу белого шума, тем самым размывая спектр ошибки квантования по всему диапазону частот. В основе конструкции лежит метод, согласно которому ошибку квантования, которая по предположению является БШ, добавляют к входному сигналу аналогично (5.22), тем самым обеспечивая её же размывание по частоте. Структурная схема подобной модели изображена на рис. 5.3. Элемент задержки введён в схему для того, чтобы она соответствовала работе реального АЦП, потому что это устройство является тактируемым. Изменение полярности ошибки применяется для удобства.

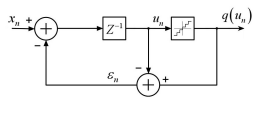
Рис. 5.3. Основа конструкции .

Из рис. 5.3 можно получить разностное уравнение

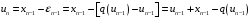. (5.23)

На рис. 5.4 приведена наиболее распространённая структурная схема 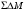с одним кольцом, которая легко получается из схемы на рис. 5.3 с помощью преобразований сумматоров [22]. На входе схемы расположен вычитатель квантованного сигнала 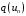из входного . После вычитателя расположен цифровой интегратор, выделенный штриховой линией. После интегратора сигнал подвергается квантованию и затем через кольцо обратной связи поступает на вычитатель.

Рис. 5.4. Структурная схема .

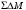Из (5.2) получим выражения

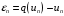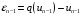, . (5.24)

Тогда с помощью (5.23), (5.24) получим

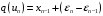. (5.25)

Таким образом, на выходе 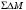сигнал представляет собой смесь задержанного входного сигнала и разности ошибок квантования за текущий такт и предыдущий. Основная задача анализа уравнения (5.25) состоит в исследовании спектра ошибки, т.к. для её устранения необходима фильтрация.

При условии (5.6) с учётом (5.23) ошибка преобразуется к виду

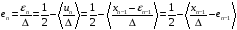. (5.26)

Формула (5.26) представляет собой рекурсивное уравнение ошибки.

Обозначим начальные условия 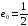и сделаем замену

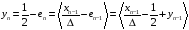. (5.27)

Поскольку в определении 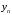участвует лишь дробная часть, т.е. 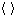, то в скобках можно прибавить 1. Тогда из (5.27) получим

. (5.28)

При этом .

Из (5.28) находим

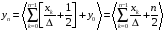. (5.29)

Ошибка квантования по (5.27), (5.29) имеет вид

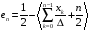. (5.30)

Стоит отметить, что выражение (5.30) по своей структуре аналогично (5.6), поэтому, произведя замену

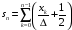, (5.31)

получим аналог (5.6), т.е.

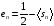. (5.32)

При этом 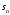в 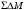является аналогом 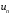в АЦП, т.е. является интегратором суммы входного сигнала и константы .

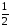5.4. Спектральные характеристики при постоянном входном воздействии.

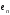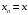Рассчитаем статистические характеристики сигнала ошибки при для 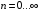, причём не вызывает переполнения и в общем случае 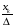является иррациональным числом [24-26]. Стоит отметить, что в случае рационального 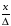, например 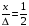, ошибка является периодической функцией с заранее известным периодом. Поскольку сигнал является медленно изменяющейся функцией, то условие передискретизации выполняется.

Из (5.31), (5.32) следует, что с каждым тактом дискретизации возрастает на величину 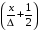, т.е. имеет место линейная зависимость

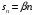, (5.33)

где . Тогда из (5.18) с учётом (5.33) получим характеристическую функцию сигнала 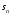в виде

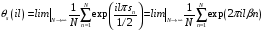. (5.34)

Поскольку для экспоненты справедливо равенство

,

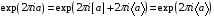которое означает, что аргумент, кратный , не влияет на результат вычисления, то из (5.34) получим

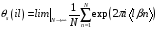. (5.35)

В работе [29] показано, что для интегрируемой функции 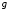справедливо равенство

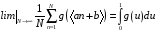
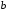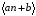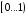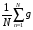при условии, что является иррациональным числом, а - действительным. Такое равенство вполне понятно интуитивно, т.к. - генератор равномерно распределённой случайной величины (СВ) на интервале , а - математическое ожидание 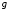на заданном интервале.

Поэтому из (5.35) получим

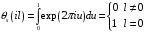. (5.36)

Причём 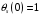можно найти из выражения (5.35).

Тогда из (5.20) для 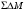получим

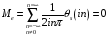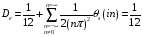, . (5.37)

Из (5.37) следует, что среднее значение и мощность ошибки 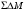такие же, как у равномерно распределённой СВ, т.е. соответствуют характеристикам шума квантования в обычном устройстве квантования. Остаётся лишь найти её спектральные характеристики.

Из (5.19) находим

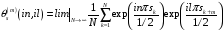, (5.38)

Тогда из (5.33) получим

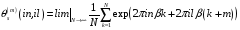
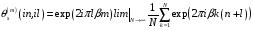
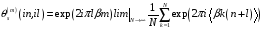. (5.39)

Таким образом, выражение (5.39) преобразуется к виду

. (5.40)

С помощью (5.21) находим корреляционную функцию (КФ) ошибки 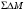в виде

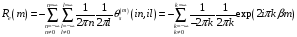. (5.41)

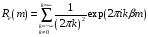. (5.42)

Как известно, по теореме Винера-Хинчина корреляционная функция и спектральная плотность мощности (СПМ) связаны парой преобразований Фурье, поэтому выражение (5.42) представляет собой синтез КФ по гармоникам с частотами 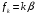и мощностями согласно (5.7).

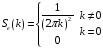. (5.43)

Из (5.42) следует, что спектр ошибки является дискретным и периодическим.

Поскольку условие т. Котельникова не выполняется для спектра ошибки, т.е. имеет место перекрытие, то при рассмотрении области частот 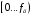следует учитывать влияние копий спектра. Поэтому в заданном диапазоне гармоники находятся на частотах

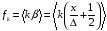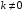при . (5.44)

Таким образом, положение гармоник в спектре ошибки зависит только от амплитуды входного сигнала.