2.2. Плотность распределения вероятности рассогласования.

Одной из основных характеристик системы является плотность распределения вероятностей (ПРВ) рассогласования .

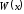В аналитических расчётах используется метод, согласно которому искомое распределение является решением уравнения ФПК, которое в стационарном режиме имеет вид

,

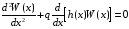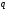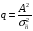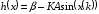где - ОСШ, которое может быть рассчитано как , а [11].

Несмотря на то, что уравнение и его решение получены для непрерывных систем, можно воспользоваться результатами, если принять шаг дискретизации по времени достаточно малым. Такое допущение имеет право на существование, потому что в главе рассматривается бесфильтровая ФАС, в которой текущее состояние системы определяется только предыдущим состоянием и входным воздействием.

Решить аналитически уравнение ФПК достаточно трудно, поэтому решение удобно представить в виде ряда Фурье

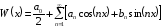, (3)

коэффициенты которого рассчитываются с помощью модифицированной функции Бесселя .

Для упрощения расчётов и проверки аналитических зависимостей приравняем в уравнении (2.2) параметры 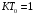, 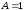и обозначим нормированную расстройку 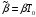. Перепишем уравнение с учётом введённых обозначений

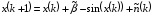. (2.4)

Таким образом, уравнение записано относительно безразмерных величин.

Тогда при условии 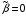получим

.

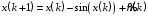При малых значениях ОСШ и отсутствии частотной расстройки справедливо равенство

,

которое в пределе принимает форму [11], т.е.

.

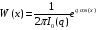Рис. 2.2. Зависимость , полученная

моделированием (линия с прямоугольником) и

расчётом (линия с окружностью).

Произведём параллельно моделирование и расчёт при заданных параметрах и 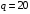дБ.

На рис. 2.2. построены две ПРВ 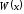, полученные моделированием (линия с прямоугольником) и аналитическим расчётом (линия с окружностью).

Из графика видно, что в достаточно большой окрестности 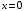кривые совпадают, т.е. формулы дают достоверный результат.

При наличии частотной расстройки, т.е. при значениях 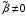расчёты намного усложняются.

Принцип работы бесфильтровой системы в режиме частотной расстройки без шума заключается в следующем. Пусть в начальный момент времени начальные фазы полезного сигнала и УГ совпадают, тогда 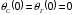. Детектор измеряет разницу фаз опорного колебания и УГ и прибавляет её к фазе УГ. Разница 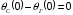, поэтому , и фаза УГ не изменяется, т.е. 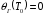. Фаза полезного сигнала изменится на 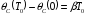и станет 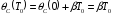. В этом случае детектор определит разницу 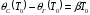и произойдёт коррекция фазы УГ, т.е. 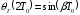, однако 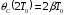, и разница на выходе детектора составит .

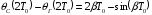Тогд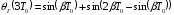а , а .

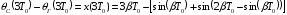Таким образом, процесс будет повторяться с каждым тактом, и при 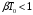за счёт чередования «+» и «-» в формуле получим

.

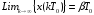Все дальнейшие рассуждения проведены относительно уравнения (2.4).

ПРВ в переходном режиме рассчитывается по разностной схеме, согласно которой производные заменяются разностями, т.е.

,

,

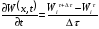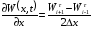где параметры 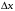и 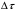задают точность вычислений по времени и фазе соответственно [11]. Рассмотрим 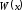в стационарном режиме, т.е. когда все переходные процессы закончились. Для этого не будем последовательно решать разностную задачу по отысканию 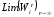, воспользуемся представленной ранее формулой разложения 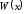в ряд (2.3). Вычисление коэффициентов напрямую представляет собой трудоёмкую задачу, однако для расчёта можно воспользоваться рекуррентными соотношениями, что заметно упрощает решение. Эти разностные уравнения имеют вид

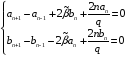
и решаются при начальных условиях 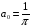, 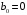[11]. Для решения системы необходимо знать 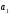и 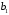, вычисление которых удобно производить по приближённым формулам. При малых значениях 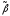коэффициенты могут быть найдены как

,

.

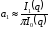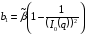Построим ПРВ рассогласования при значении 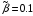, исходя из приближённых формул, и сравним их с результатом моделирования.

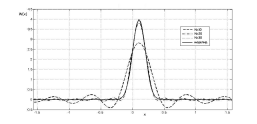
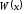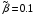Рис. 2.3. Зависимость при , полученная

моделированием (сплошная линия) и расчётом при значениях