
- •Содержание
- •Глава 1. Нелинейная динамика синтезатора частот с петлёй фап………………………………………………………………………………..4
- •Глава 2. Анализ бесфильтровой дискретной системы фазовой автоподстройки при наличии нормального белого шума…………...……23
- •Глава 3. Сравнительный анализ цифровых систем синхронизации………………………………………………………………….41
- •Глава 4. Цифровые системы синхронизации с перестраивающимися параметрами…………………………………………62
- •Глава 5. Анализ сигма-дельта модулятора с одной петлёй……..….79
- •Введение
- •Глава 1 Нелинейная динамика синтезатора частот с петлёй фап.
- •1.1. Анализ бесфильтровой системы ифапч.
- •1.2. Моделирование системы ифапч с ичфд и фильтром второго порядка в частотном режиме.
- •1.3. Устойчивость системы ифапч.
- •1.4. Синтез оптимальной по устойчивости и быстродействию структуры синтезатора.
- •1.5. Переходной процесс синтезатора частот с петлёй фап.
- •Глава 2. Анализ бесфильтровой дискретной системы фазовой автоподстройки при наличии нормального белого шума.
- •2.1. Математическая модель системы Импульсной Фазовой Автоподстройки (ифап).
- •2.2. Плотность распределения вероятности рассогласования.
- •10 (Штриховая линия),
- •20 (Штрих - пунктирная линия линия),
- •30 (Пунктирная линия).
- •10 (Штрих - пунктирная линия),
- •20 (Штриховая линия),
- •30 (Пунктирная линия).
- •3 (Пунктирная линия),
- •4 (Штрих - пунктирная линия),
- •5 (Штриховая линия).
- •5 (Пунктирная линия),
- •10 (Штрих - пунктирная линия),
- •15 (Штриховая линия).
- •2.3. Анализ срыва слежения.
- •2.3.1. Расчёт среднего времени до срыва слежения.
- •2.3.2. Расчёт вероятности срыва слежения.
- •2 (Сплошная линия),
- •4 (Штриховая линия) и
- •8 (Штрих - пунктирная линия).
- •Глава 3. Сравнительный анализ цифровых систем синхронизации.
- •3.1. Структура математической модели цсс.
- •3.2. Схема Холмса.
- •3.3. Схема Осатаке-Огавы.
- •3.4. Схема Кессны - Леви.
- •3.4.1. Фильтр случайных блужданий.
- •Глава 4. Цифровые системы синхронизации с перестраивающимися параметрами.
- •4.1. Структура модели цсс.
- •4.2. Модель схемы Кессны - Леви.
- •4.3. Цсс с перестроением параметров.
- •4.3.1. Целевая функция.
- •4.3.2. Принцип построения системы.
- •4.3.3. Реализация системы.
- •4.4. Полоса захвата системы с постоянными параметрами.
- •4.5. Применение цсс с перестроением параметров.
- •Глава 5. Анализ сигма-дельта модулятора с одной петлёй.
- •5.1. Математическая модель устройства квантования.
- •5.2. Статистические характеристики ошибки квантования.
- •5.3. Модель с одной петлёй.
- •5.4. Спектральные характеристики при постоянном входном воздействии.
- •5.5. Моделирование работы при постоянном входном воздействии.
- •Список использованных источников
1.2. Моделирование системы ифапч с ичфд и фильтром второго порядка в частотном режиме.
Дискриминатор типа ИЧФДЗ на двух триггерах в частотном режиме работает практически без пауз, а в фазовом - как обычный дискриминатор с широтно-импульсной модуляцией (ШИМ). Применяемый ФНЧ является суммарным преобразователем «временной интервал-напряжение» за счет заряда от источников тока эквивалентной емкостной составляющей [5,6]. В общем случае такая система является нелинейной, так как в ней имеется ШИМ.
Одним из возможных методов анализа работы ИФАПЧ является имитационное моделирование. Модель позволяет оценить такие важные характеристики нелинейной системы как переходный процесс и устойчивость, причём без каких-либо допущений. С её помощью можно проверить результаты расчётов, оценить точность приближений, а также вычислить параметры, анализ которых аналитическими методами затруднён.
В
качестве примера зададим параметры
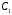 =0.01мкф,
=0.01мкф,
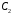 =0.001мкф,
=0.001мкф,
 =500
Ом,
=500
Ом,
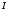 =4
мА,
=4
мА,
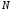 =2,
=2,
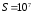 Гц/В,
Гц/В,
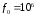 Гц, тогда получим расчётное значение
Гц, тогда получим расчётное значение
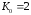 по формуле (1.6) для линейного СЧ без
фильтра (граница устойчивости). При
моделировании можно убедится, что
система неустойчива, т.к. модель нелинейная
и фильтр вносит свои изменения. Методом
последовательных приближений находим,
что система устойчива при
по формуле (1.6) для линейного СЧ без
фильтра (граница устойчивости). При
моделировании можно убедится, что
система неустойчива, т.к. модель нелинейная
и фильтр вносит свои изменения. Методом
последовательных приближений находим,
что система устойчива при
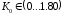 .
Оставим все параметры системы, кроме
.
Оставим все параметры системы, кроме
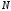 ,
без изменения. На рис. 1.2 показан процесс
изменения напряжения на фильтре при
переключении ДПКД из
,
без изменения. На рис. 1.2 показан процесс
изменения напряжения на фильтре при
переключении ДПКД из
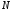 =6
в
=6
в
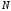 =12.
Из эпюры напряжения видно, что при
=12.
Из эпюры напряжения видно, что при
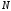 =6
система находится на границе устойчивости,
хотя это граница представляет собой не
конкретное значение
=6
система находится на границе устойчивости,
хотя это граница представляет собой не
конкретное значение
 ,
а некоторый диапазон (в данном случае
при
,
а некоторый диапазон (в данном случае
при
 на фильтре наблюдаются периодические
колебания).
на фильтре наблюдаются периодические
колебания).
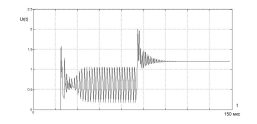
Рис. 1.2. Процесс
изменения напряжения на фильтре при
переключении ДПКД из
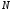 =6
в
=6
в
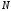 =12.
=12.
На рис. 1.3 показан
процесс изменения напряжения на фильтре
при переключении ДПКД из значения
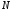 =32
в
=32
в
 =64
и обратно. Из эпюры напряжения видно,
что переходные процессы установления
напряжения отличаются по типу и имеют
разную длительность.
=64
и обратно. Из эпюры напряжения видно,
что переходные процессы установления
напряжения отличаются по типу и имеют
разную длительность.
Рис. 1.3. Процесс
изменения напряжения на фильтре при
переключении ДПКД из значения
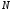 =32
в
=32
в
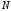 =64
и обратно.
=64
и обратно.
В зарубежных и отечественных публикациях [1,3,8,9] появилось достаточно много публикаций по проектированию колец ИФАПЧ, где критерием выбора параметров является полоса пропускания. В этих работах кольца ИФАПЧ рассматриваются как непрерывные, хотя, как правило, имеют место компоненты дискретного характера. Так, использование импульсного частотно-фазового детектора (ИЧФД), который рассматривается в них в качестве дискриминатора, допускает применение методов непрерывного анализа с некоторыми ограничениями.
Для построения частотных характеристик воспользуемся результатами [7]. Для режима малых отклонений от положения равновесия, когда система считается линейной, приведено аналитическое выражение передаточной функции разомкнутой системы по фазе, непрерывная часть которой при условии (1.1) имеет вид:
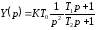 ,
(1.7)
,
(1.7)
где
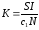 - коэффициент усиления разомкнутой
системы.
- коэффициент усиления разомкнутой
системы.
Применим
 - преобразование к формуле (1.7), согласно
которому
- преобразование к формуле (1.7), согласно
которому
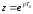 ,
получим
,
получим
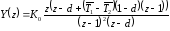 ,
,
где
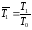 ,
,
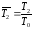 ,
а
,
а
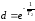 .
.
Применим
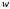 - преобразование к формуле (1.7), согласно
которому
- преобразование к формуле (1.7), согласно
которому
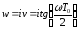 ,
получим
,
получим
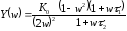 ,
(1.8)
,
(1.8)
где
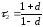 ,
а
,
а
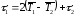 .
.
Как известно, для замкнутых автоматических систем справедливо соотношение
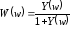 ,
,
где
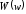 - передаточная функция замкнутой системы,
а
- передаточная функция замкнутой системы,
а
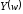 - передаточная функция разомкнутой
системы. Таким образом, для анализа
устойчивости можно рассматривать не
замкнутую систему
- передаточная функция разомкнутой
системы. Таким образом, для анализа
устойчивости можно рассматривать не
замкнутую систему
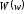 ,
а разомкнутую
,
а разомкнутую
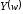 .
Для этого разработаны стандартные
критерии. Например, критерий Михайлова
использует годограф передаточной
функции разомкнутой системы, а критерий
Гурвица основан на анализе характеристического
полинома передаточной функции замкнутой
системы.
.
Для этого разработаны стандартные
критерии. Например, критерий Михайлова
использует годограф передаточной
функции разомкнутой системы, а критерий
Гурвица основан на анализе характеристического
полинома передаточной функции замкнутой
системы.
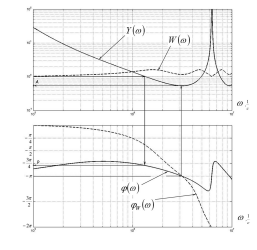
Рис. 1.4. Зависимости
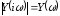 ,
,
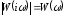 ,
а также
,
а также
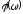 ,
,
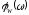 ,
т.е. ЧХ разомкнутой и замкнутой систем
соответственно.
,
т.е. ЧХ разомкнутой и замкнутой систем
соответственно.
Оставим параметры
синтезатора
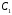 =0.01мкф,
=0.01мкф,
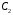 =0.001мкф,
=0.001мкф,
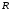 =500
Ом,
=500
Ом,
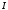 =4
мА,
=4
мА,
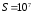 Гц/В,
Гц/В,
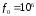 Гц без изменений, но используем
Гц без изменений, но используем
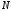 =16,
получим значение
=16,
получим значение
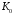 =0.25.
При этом
=0.25.
При этом
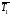 =5.5,
=5.5,
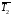 =0.5,
тогда
=0.5,
тогда
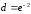 .
Рассчитаем
.
Рассчитаем
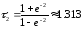 и
и
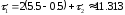 .
.
На рис. 4 представлены
зависимости
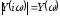 ,
,
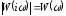 ,
а также
,
а также
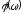 ,
,
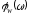 ,
т.е. ЧХ разомкнутой и замкнутой систем
соответственно.
,
т.е. ЧХ разомкнутой и замкнутой систем
соответственно.
