
- •Содержание
- •Глава 1. Нелинейная динамика синтезатора частот с петлёй фап………………………………………………………………………………..4
- •Глава 2. Анализ бесфильтровой дискретной системы фазовой автоподстройки при наличии нормального белого шума…………...……23
- •Глава 3. Сравнительный анализ цифровых систем синхронизации………………………………………………………………….41
- •Глава 4. Цифровые системы синхронизации с перестраивающимися параметрами…………………………………………62
- •Глава 5. Анализ сигма-дельта модулятора с одной петлёй……..….79
- •Введение
- •Глава 1 Нелинейная динамика синтезатора частот с петлёй фап.
- •1.1. Анализ бесфильтровой системы ифапч.
- •1.2. Моделирование системы ифапч с ичфд и фильтром второго порядка в частотном режиме.
- •1.3. Устойчивость системы ифапч.
- •1.4. Синтез оптимальной по устойчивости и быстродействию структуры синтезатора.
- •1.5. Переходной процесс синтезатора частот с петлёй фап.
- •Глава 2. Анализ бесфильтровой дискретной системы фазовой автоподстройки при наличии нормального белого шума.
- •2.1. Математическая модель системы Импульсной Фазовой Автоподстройки (ифап).
- •2.2. Плотность распределения вероятности рассогласования.
- •10 (Штриховая линия),
- •20 (Штрих - пунктирная линия линия),
- •30 (Пунктирная линия).
- •10 (Штрих - пунктирная линия),
- •20 (Штриховая линия),
- •30 (Пунктирная линия).
- •3 (Пунктирная линия),
- •4 (Штрих - пунктирная линия),
- •5 (Штриховая линия).
- •5 (Пунктирная линия),
- •10 (Штрих - пунктирная линия),
- •15 (Штриховая линия).
- •2.3. Анализ срыва слежения.
- •2.3.1. Расчёт среднего времени до срыва слежения.
- •2.3.2. Расчёт вероятности срыва слежения.
- •2 (Сплошная линия),
- •4 (Штриховая линия) и
- •8 (Штрих - пунктирная линия).
- •Глава 3. Сравнительный анализ цифровых систем синхронизации.
- •3.1. Структура математической модели цсс.
- •3.2. Схема Холмса.
- •3.3. Схема Осатаке-Огавы.
- •3.4. Схема Кессны - Леви.
- •3.4.1. Фильтр случайных блужданий.
- •Глава 4. Цифровые системы синхронизации с перестраивающимися параметрами.
- •4.1. Структура модели цсс.
- •4.2. Модель схемы Кессны - Леви.
- •4.3. Цсс с перестроением параметров.
- •4.3.1. Целевая функция.
- •4.3.2. Принцип построения системы.
- •4.3.3. Реализация системы.
- •4.4. Полоса захвата системы с постоянными параметрами.
- •4.5. Применение цсс с перестроением параметров.
- •Глава 5. Анализ сигма-дельта модулятора с одной петлёй.
- •5.1. Математическая модель устройства квантования.
- •5.2. Статистические характеристики ошибки квантования.
- •5.3. Модель с одной петлёй.
- •5.4. Спектральные характеристики при постоянном входном воздействии.
- •5.5. Моделирование работы при постоянном входном воздействии.
- •Список использованных источников
Глава 1 Нелинейная динамика синтезатора частот с петлёй фап.
Построена нелинейная имитационная модель системы импульсно-фазовой автоподстройки частоты (ИФАПЧ) с широтно-импульсным фазовым детектором и фильтром 2-го порядка. Определены границы устойчивости и длительность переходного процесса. Построены частотные характеристики разомкнутой и замкнутой петли ФАП. Найдены параметры системы с учётом запасов устойчивости по амплитуде и фазе. Даны рекомендации по проектированию синтезатора при оптимальном соотношении запасов устойчивости и быстродействия.
Вопросам теории
нелинейных систем ИФАПЧ с ИЧФД и фильтром
2-го порядка проявляется повышенный
интерес, так как такие системы в последнее
время находят весьма широкое применение.
Поэтому вопросу анализа спектральных
и динамических характеристик данных
систем посвящено достаточно много
публикаций. Например, анализ динамических
характеристик синтезаторов, построенных
на основе систем ИФАПЧ с широтно-импульсным
частотно-фазовым детектором (IIIИЧФД) и
фильтром второго порядка, проводится
в публикациях [1,2,5,6]. Однако динамика в
данных работах либо описывается
достаточно сложными математическими
выражениями, что затрудняет их наглядность
[1], либо проводится с некоторыми
ограничениями для режимов больших и
малых отклонений от положения равновесия.
Такие ограничения могут несколько
искажать картину процесса установления
системы как при больших отклонений от
положения равновесия, так и в режиме
устойчивости в малом. Кроме того, в
большинстве публикаций не рассматривается
реальная динамика процесса установления
с одного края диапазона на другой при
переключении коэффициентов деления
делителя с переменным коэффициентом
деления (ДПКД) в цепи обратной связи.
Такое рассмотрение процесса установления
весьма важно, так как в этом случае
наблюдается смещение рабочей точки по
модуляционной характеристике управляемого
генератора (УГ). При этом можно определить,
выходит ли характеристика регулирования
за пределы линейного участка
дискриминационной характеристики
ШИЧФД, так как выход рабочей точки за
пределы участка напряжений
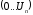 может привести к разрыву петли ИФАПЧ
(
может привести к разрыву петли ИФАПЧ
(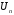 - напряжение питания выходных цепей
ШИЧФД) и срыву синхронизации. В работе
[2] представлен достаточно наглядный
алгоритм динамики процесса установления
системы с учетом влияния коэффициентов
деления ДПКД, однако в ней не учитывалось
влияние фильтра второго порядка. Поэтому
построение модели, которая как можно
ближе отображает динамику работы системы
ИФАПЧ с фильтром второго порядка,
является весьма актуальной задачей.
- напряжение питания выходных цепей
ШИЧФД) и срыву синхронизации. В работе
[2] представлен достаточно наглядный
алгоритм динамики процесса установления
системы с учетом влияния коэффициентов
деления ДПКД, однако в ней не учитывалось
влияние фильтра второго порядка. Поэтому
построение модели, которая как можно
ближе отображает динамику работы системы
ИФАПЧ с фильтром второго порядка,
является весьма актуальной задачей.
1.1. Анализ бесфильтровой системы ифапч.
Обобщенная структурная схема системы представлена на рис. 1.1, где ФНЧ - фильтр нижних частот; УГ - управляемый генератор; ДПКД - делитель с переменным коэффициентом деления; ГТ - генератор тока; Кл – ключ; Т – триггер[1]. В качестве ИЧФД был выбран дискриминатор с тремя состояниями ИЧФД3. Работа такой системы описана в [2].
Передаточная функция ФНЧ равна
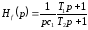 ,
(1.1)
,
(1.1)
где
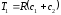 ,
а
,
а
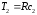 ,
,
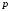 -
оператор преобразования Лапласа. Такой
фильтр следует считать фильтром 2-го
порядка. Как уже отмечалось, в [2] для
анализа динамических характеристик
синтезаторов частот с ИФАПЧ исследовались
характеристики бесфильтровых
линеаризованных систем, т.е. систем, в
которых
-
оператор преобразования Лапласа. Такой
фильтр следует считать фильтром 2-го
порядка. Как уже отмечалось, в [2] для
анализа динамических характеристик
синтезаторов частот с ИФАПЧ исследовались
характеристики бесфильтровых
линеаризованных систем, т.е. систем, в
которых
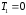 и
и
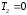 ,
тогда
,
тогда
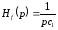 .
Одним из способов визуализации переходного
процесса установления колебаний является
графо-аналитический метод, который
позволяет рассмотреть динамику системы
без фильтра[2]. Рассмотрим переключение
кода в подобной системе.
.
Одним из способов визуализации переходного
процесса установления колебаний является
графо-аналитический метод, который
позволяет рассмотреть динамику системы
без фильтра[2]. Рассмотрим переключение
кода в подобной системе.

Рис. 1.1. Обобщенная структурная схема системы ИФАПЧ с фильтром второго порядка, на которой ФНЧ - фильтр нижних частот; УГ - управляемый генератор; ДПКД - делитель с переменным коэффициентом деления; ГТ - генератор тока; Кл – ключ; Т – триггер.
Введём обозначения
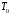 - период повторения опорного сигнала,
- период повторения опорного сигнала,
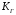 - коэффициент передачи УГ,
- коэффициент передачи УГ,
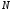 - коэффициент деления ДПКД,
- коэффициент деления ДПКД,
 -
коэффициент передачи ИЧФД и ФНЧ. Пусть
коэффициент передачи ДПКД изменяется
с
-
коэффициент передачи ИЧФД и ФНЧ. Пусть
коэффициент передачи ДПКД изменяется
с
 на
на
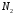 ,
тогда напряжение на фильтре станет
,
тогда напряжение на фильтре станет
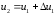 ,
(1.2)
,
(1.2)
где
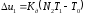 - приращение УГ в момент переключения.
В установившемся режиме справедливо
равенство
- приращение УГ в момент переключения.
В установившемся режиме справедливо
равенство
 ,
,
поэтому
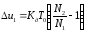 ,
(1.3)
,
(1.3)
В дальнейшем процесс будет повторяться и разностное уравнение с учётом (1.2) и (1.3) примет вид
 ,
(1.4)
,
(1.4)
где
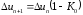 ,
а
,
а
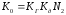 - коэффициент усиления разомкнутой
системы [1,2]. Таким образом, из (1.4) следует,
что
- коэффициент усиления разомкнутой
системы [1,2]. Таким образом, из (1.4) следует,
что
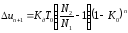 ,
(1.5)
,
(1.5)
Динамические
характеристики определяются устойчивостью
ИФАПЧ, параметрами переходного процесса
[3,4]. Определим границы устойчивости «в
малом». Для того чтобы система была
устойчива «в малом» т.е. была способна
возвращаться в стационарный режим при
малых отклонениях, необходимо выполнение
условия
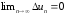 .
Тогда из (1.5) получим, что система устойчива
при
.
Тогда из (1.5) получим, что система устойчива
при
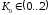 .
Коэффициент усиления
.
Коэффициент усиления
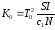 ,
(1.6)
,
(1.6)
где
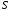 - крутизна характеристики УГ [Гц/В]. Для
анализа устойчивости «в малом» непрерывных
систем развит ряд критериев: Рауса -
Гурвица, Найквиста, Михайлова. Например,
анализ устойчивости ИФАПЧ по критерию
Рауса – Гурвица выполняется посредством
решения системы уравнений типа
«неравенство». Причём если ФНЧ имеет
порядок 0 (ФНЧ отсутствует), то система
содержит 2 неравенства, если же ФНЧ имеет
порядок 2 (рис. 1.1), то их количество
возрастает до 5, а при дальнейшем росте
порядка сложность условий резко
возрастает.
- крутизна характеристики УГ [Гц/В]. Для
анализа устойчивости «в малом» непрерывных
систем развит ряд критериев: Рауса -
Гурвица, Найквиста, Михайлова. Например,
анализ устойчивости ИФАПЧ по критерию
Рауса – Гурвица выполняется посредством
решения системы уравнений типа
«неравенство». Причём если ФНЧ имеет
порядок 0 (ФНЧ отсутствует), то система
содержит 2 неравенства, если же ФНЧ имеет
порядок 2 (рис. 1.1), то их количество
возрастает до 5, а при дальнейшем росте
порядка сложность условий резко
возрастает.
В режимах, когда включается СЧ или переключаются коэффициенты деления, возможны достаточно большие отклонения от положения равновесия. Как известно из [1,3], в таких режимах для выяснения условий устойчивости ИФАПЧ «в целом» линейные приближения не могут быть использованы и должна быть проанализирована система нелинейных разностных уравнений с учетом алгоритмов функционирования дискриминаторов. Поскольку решение этих уравнений в аналитической форме выражается сложными формулами, его исследуют с помощью ЭВМ, либо приближенными методами анализа. Результаты изучения ИФАПЧ с ИЧФД и различными ФНЧ позволяют утверждать, что введение импульсного ЧД приводит к устойчивости системы «в целом», если она обладает устойчивостью «в малом» [1,3].
Одной из основных
характеристик СЧ является переходной
процесс, возникающий при переключении
коэффициента деления. Основным показателем
переходного процесса является его
длительность, которая часто измеряется
в периодах опорного колебания
 ,
по истечении которых выполняется
неравенство
,
по истечении которых выполняется
неравенство
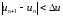 ,
где
,
где
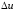 характеризует точность установления
[1]. Для оценки быстродействия с учётом
(1.4) введём параметр
характеризует точность установления
[1]. Для оценки быстродействия с учётом
(1.4) введём параметр
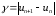 ,
тогда в случае бесфильтровой линеаризованной
системы получим
,
тогда в случае бесфильтровой линеаризованной
системы получим
 .
.
Как известно [1], анализ переходного процесса системы с фильтром в частотном режиме связан с разложением передаточной функции по отношению к ошибке на элементарные дроби, нахождением их оригиналов во временной области и последующим анализом. При этом система предполагается линейной и непрерывной. Такой метод является не только приближённым, но и неточным, т.к. происходит потеря данных при ограничении ряда. Следует отметить, что в фазовом режиме переходной процесс описывается более сложными аналитическими выражениями.
