
- •CONTENTS
- •Preface
- •To the Student
- •Diagnostic Tests
- •1.1 Four Ways to Represent a Function
- •1.2 Mathematical Models: A Catalog of Essential Functions
- •1.3 New Functions from Old Functions
- •1.4 Graphing Calculators and Computers
- •1.6 Inverse Functions and Logarithms
- •Review
- •2.1 The Tangent and Velocity Problems
- •2.2 The Limit of a Function
- •2.3 Calculating Limits Using the Limit Laws
- •2.4 The Precise Definition of a Limit
- •2.5 Continuity
- •2.6 Limits at Infinity; Horizontal Asymptotes
- •2.7 Derivatives and Rates of Change
- •Review
- •3.2 The Product and Quotient Rules
- •3.3 Derivatives of Trigonometric Functions
- •3.4 The Chain Rule
- •3.5 Implicit Differentiation
- •3.6 Derivatives of Logarithmic Functions
- •3.7 Rates of Change in the Natural and Social Sciences
- •3.8 Exponential Growth and Decay
- •3.9 Related Rates
- •3.10 Linear Approximations and Differentials
- •3.11 Hyperbolic Functions
- •Review
- •4.1 Maximum and Minimum Values
- •4.2 The Mean Value Theorem
- •4.3 How Derivatives Affect the Shape of a Graph
- •4.5 Summary of Curve Sketching
- •4.7 Optimization Problems
- •Review
- •5 INTEGRALS
- •5.1 Areas and Distances
- •5.2 The Definite Integral
- •5.3 The Fundamental Theorem of Calculus
- •5.4 Indefinite Integrals and the Net Change Theorem
- •5.5 The Substitution Rule
- •6.1 Areas between Curves
- •6.2 Volumes
- •6.3 Volumes by Cylindrical Shells
- •6.4 Work
- •6.5 Average Value of a Function
- •Review
- •7.1 Integration by Parts
- •7.2 Trigonometric Integrals
- •7.3 Trigonometric Substitution
- •7.4 Integration of Rational Functions by Partial Fractions
- •7.5 Strategy for Integration
- •7.6 Integration Using Tables and Computer Algebra Systems
- •7.7 Approximate Integration
- •7.8 Improper Integrals
- •Review
- •8.1 Arc Length
- •8.2 Area of a Surface of Revolution
- •8.3 Applications to Physics and Engineering
- •8.4 Applications to Economics and Biology
- •8.5 Probability
- •Review
- •9.1 Modeling with Differential Equations
- •9.2 Direction Fields and Euler’s Method
- •9.3 Separable Equations
- •9.4 Models for Population Growth
- •9.5 Linear Equations
- •9.6 Predator-Prey Systems
- •Review
- •10.1 Curves Defined by Parametric Equations
- •10.2 Calculus with Parametric Curves
- •10.3 Polar Coordinates
- •10.4 Areas and Lengths in Polar Coordinates
- •10.5 Conic Sections
- •10.6 Conic Sections in Polar Coordinates
- •Review
- •11.1 Sequences
- •11.2 Series
- •11.3 The Integral Test and Estimates of Sums
- •11.4 The Comparison Tests
- •11.5 Alternating Series
- •11.6 Absolute Convergence and the Ratio and Root Tests
- •11.7 Strategy for Testing Series
- •11.8 Power Series
- •11.9 Representations of Functions as Power Series
- •11.10 Taylor and Maclaurin Series
- •11.11 Applications of Taylor Polynomials
- •Review
- •APPENDIXES
- •A Numbers, Inequalities, and Absolute Values
- •B Coordinate Geometry and Lines
- •E Sigma Notation
- •F Proofs of Theorems
- •G The Logarithm Defined as an Integral
- •INDEX

67–69
|
|
67. |
y |
|
|
68. |
y |
|
|
69. |
y |
Prove the formula, where m and n are positive integers.
sin mx cos nx dx 0 |
|
||
sin mx sin nx dx |
|
0 |
if m n |
|
|
if m n |
|
cos mx cos nx dx |
0 |
if m n |
|
|
|
|
if m n |
SECTION 7.3 TRIGONOMETRIC SUBSTITUTION |||| 467
70. A finite Fourier series is given by the sum
N
f x an sin nx
n 1
a1 sin x a2 sin 2x aN sin Nx
Show that the mth coefficient am is given by the formula
|
1 |
|
|
|
am |
y |
f x sin mx dx |
||
|
 7.3 TRIGONOMETRIC SUBSTITUTION
7.3 TRIGONOMETRIC SUBSTITUTION
In finding the area of a circle or an ellipse, an integral of the form xsa 2 x 2 dx arises,
where a 0. If it were xx sa 2 x 2 dx, the substitution u a 2 x 2 would be effective
but, as it stands, xsa 2 x 2 dx is more difficult. If we change the variable from x to by the substitution x a sin , then the identity 1 sin2 cos2 allows us to get rid of the root sign because
sa 2 x 2 sa 2 a 2 sin2 sa 2 1 sin2 sa 2 cos2 a cos
Notice the difference between the substitution u a 2 x 2 (in which the new variable is a function of the old one) and the substitution x a sin (the old variable is a function of the new one).
In general we can make a substitution of the form x t t by using the Substitution Rule in reverse. To make our calculations simpler, we assume that t has an inverse function; that is, t is one-to-one. In this case, if we replace u by x and x by t in the Substitution Rule (Equation 5.5.4), we obtain
yf x dx yf t t t t dt
This kind of substitution is called inverse substitution.
We can make the inverse substitution x a sin provided that it defines a one-to-one
function. This can be accomplished by restricting to lie in the interval 2, |
2 . |
In the following table we list trigonometric substitutions that are effective for the given radical expressions because of the specified trigonometric identities. In each case the restriction on is imposed to ensure that the function that defines the substitution is one-to-one. (These are the same intervals used in Section 1.6 in defining the inverse functions.)
TABLE OF TRIGONOMETRIC SUBSTITUTIONS
Expression |
|
Substitution |
|
|
|
|
Identity |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sa 2 |
x 2 |
x a sin , |
|
|
|
|
|
|
|
|
|
|
1 |
sin2 |
cos2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sa 2 |
x 2 |
x a tan , |
|
|
|
|
|
|
|
|
1 |
tan2 |
sec2 |
|
||||||
|
|
|
|
|
|
|
|
|||||||||||||
2 |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
s |
|
|
x a sec , |
0 |
|
|
|
|
|
|
or |
|
3 |
|
sec2 1 tan2 |
|
||||
x 2 a 2 |
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

468 |||| CHAPTER 7 TECHNIQUES OF INTEGRATION
3
x
¨
œ„„„„9-≈„
FIGURE 1 sin ¨= x3
y
(0,b)
(a,0)
0x
FIGURE 2
≈ + ¥ =1 a@ b@
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EXAMPLE 1 Evaluate y |
s9 |
x 2 |
|
dx. |
|
|
|
|
|
|||||||||||
V |
|
|
|
|
|
|
|||||||||||||||
x 2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
SOLUTION Let x 3 sin , where 2 |
|
|
|
2. Then dx 3 cos d and |
|||||||||||||||||
|
s |
|
s |
|
|
|
|
s |
|
3 cos 3 cos |
|||||||||||
9 x 2 |
9 9 sin2 |
|
9 cos2 |
||||||||||||||||||
(Note that cos 0 because 2 |
|
|
|
|
2.) Thus the Inverse Substitution Rule |
||||||||||||||||
gives |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
3 cos |
|||||||
|
|
|
y |
|
9 x 2 |
|
dx y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 cos d |
|||||||||
|
|
|
x 2 |
|
|
|
9 sin2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
d ycot2 d |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
sin2 |
|||||||||
y csc2 1 d
cot C
Since this is an indefinite integral, we must return to the original variable x. This can be done either by using trigonometric identities to express cot in terms of sin x 3 or by drawing a diagram, as in Figure 1, where is interpreted as an angle of a right triangle. Since sin x 3, we label the opposite side and the hypotenuse as having lengths x and 3. Then the Pythagorean Theorem gives the length of the adjacent side as s9 x 2 ,
so we can simply read the value of cot |
from the figure: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cot |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(Although 0 in the diagram, this expression for cot |
is valid even when 0.) |
|
|||||||||||||||||||||||||||||||||||||
Since sin x 3, we have |
|
sin 1 x 3 and so |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
s |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
9 x 2 |
|
dx |
9 x 2 |
|
sin 1 |
|
|
|
C |
M |
||||||||||||||||||||||||
|
|
|
|
y |
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||
|
EXAMPLE 2 Find the area enclosed by the ellipse |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 2 |
|
b 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
SOLUTION Solving the equation of the ellipse for y, we get |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
y 2 |
|
|
|
x 2 |
|
|
|
a 2 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
or |
|
y |
|
sa 2 |
x 2 |
|
|||||||||||||||||||||||||||
|
|
b |
2 |
a |
2 |
|
a |
2 |
|
|
|
|
|
|
|
|
a |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Because the ellipse is symmetric with respect to both axes, the total area A is four times the area in the first quadrant (see Figure 2). The part of the ellipse in the first quadrant is given by the function
|
y |
b |
|
|
|
0 x a |
|||||
|
|
a 2 |
x 2 |
|
|||||||
|
a s |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a b |
|
|
|
||||
and so |
41 A y0 |
|
|
sa 2 |
x 2 dx |
||||||
|
a |
||||||||||

œ„„„„„≈+4
x
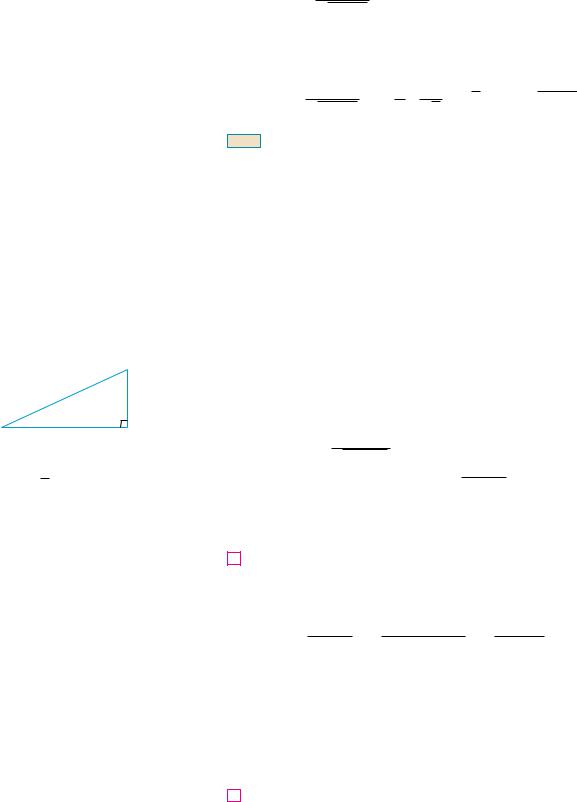
¨
2
FIGURE 3 tan ¨= x2
SECTION 7.3 TRIGONOMETRIC SUBSTITUTION |||| 469
To evaluate this integral we substitute x a sin . Then dx a cos d . To change
the limits of integration we note that when x 0, sin |
0, so 0; when x a, |
|||||||||||||||||
sin 1, so |
2. Also |
|
|
|
|
|
|
|
||||||||||
|
s |
|
s |
|
|
s |
|
a cos a cos |
||||||||||
|
a 2 x 2 |
a 2 a 2 sin2 |
a 2 cos2 |
|||||||||||||||
since 0 |
|
|
2. Therefore |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
b a |
|
|
|
|
|
|
b |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A 4 |
|
y0 |
sa 2 x 2 dx 4 |
|
y0 |
a cos a cos d |
|||||||||
|
|
|
a |
a |
||||||||||||||
|
|
|
4ab y0 |
2 cos2 d 4ab y0 2 |
21 1 cos 2 d |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2ab |
|
0 0 ab |
||||||
|
|
|
2ab[ |
21 sin 2 ]0 |
|
|||||||||||||
|
|
|
2 |
|||||||||||||||
We have shown that the area of an ellipse with semiaxes a and b is ab. In particular, |
|
taking a b r, we have proved the famous formula that the area of a circle with |
|
radius r is r 2. |
M |
NOTE Since the integral in Example 2 was a definite integral, we changed the limits of integration and did not have to convert back to the original variable x.
|
EXAMPLE 3 Find y |
1 |
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x 2s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x 2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
SOLUTION Let x 2 tan , 2 |
2. Then dx 2 sec2 d and |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
s |
|
s |
|
|
|
s |
|
|
2 sec 2 sec |
||||||||||||||||||||||||||||||||||||||||||||||
x 2 4 |
4 tan 2 1 |
|
4 sec2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Thus we have |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
2 sec2 d |
|
|
|
|
|
|
1 |
|
|
|
sec |
||||||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
d |
||||||||||||||||||||||||||||||||||
|
x 2s |
|
|
|
|
4 tan2 |
|
2 sec |
|
4 |
tan2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
x 2 4 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
To evaluate this trigonometric integral we put everything in terms of sin and cos : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sec |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
cos2 |
|
|
|
cos |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
tan2 |
|
cos |
|
|
|
sin2 |
sin2 |
|
|
|
||||||||||||||||||||||||||||||||||
Therefore, making the substitution u sin |
, we have |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
y |
|
|
|
|
|
dx |
1 |
|
y |
|
cos |
|
|
d |
|
1 |
|
y |
|
du |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x 2s |
|
|
|
|
|
|
|
4 |
|
|
sin2 |
|
|
4 |
|
|
u 2 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
x 2 4 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
C |
1 |
|
C |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
4 sin |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
csc |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We use Figure 3 to determine that csc |
s |
|
|
|
|
|
|
x and so |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
x 2 4 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
s |
x 2 4 |
|
|
C |
|
|
M |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x 2s |
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
x 2 4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
470 |||| CHAPTER 7 TECHNIQUES OF INTEGRATION
x
EXAMPLE 4 Find y sx 2 4 dx.
SOLUTION It would be possible to use the trigonometric substitution x 2 tan Example 3). But the direct substitution u x 2 4 is simpler, because then and
y sx 2x 4 dx 12 y sduu su C sx 2 4 C
here (as in du 2x dx
M
NOTE Example 4 illustrates the fact that even when trigonometric substitutions are possible, they may not give the easiest solution. You should look for a simpler method first.
EXAMPLE 5 Evaluate y |
|
dx |
, where a 0. |
|
|
||||||||||||||
s |
|
|
|
|
|||||||||||||||
x 2 a 2 |
|
|
|||||||||||||||||
SOLUTION 1 We let x a sec , where 0 |
2 or |
3 2. Then |
|||||||||||||||||
dx a sec |
tan d and |
|
|
|
|
|
|
|
|||||||||||
|
s |
|
s |
|
|
|
|
s |
|
a tan a tan |
|||||||||
|
x 2 a 2 |
a 2 sec2 |
1 |
a 2 tan2 |
|||||||||||||||
Therefore |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
a sec tan |
|
|
||||||||||
|
|
y |
|
|
|
|
|
|
|
y |
|
|
|
|
d |
|
|
||
|
s |
|
|
|
|
|
a tan |
|
|
|
|
||||||||
|
x 2 a 2 |
|
|
||||||||||||||||
ysec d ln sec tan C
x
œ„„„„„≈-a@
¨
a
FIGURE 4
x sec ¨=a
The triangle in Figure 4 gives tan
dx
y sx 2 a 2
Writing C1 C ln a, we have
s |
x |
2 a 2 |
a, so we have |
|||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|||
ln |
|
x |
|
sx 2 a 2 |
|
C |
||
|
|
|
|
|
||||
ln x sx 2 a 2 ln a C
|
y |
|
dx |
ln x s |
|
C1 |
|
1 |
|
x 2 a 2 |
|||||
s |
|
|
|||||
x 2 a 2 |
|||||||
SOLUTION 2 For x 0 the hyperbolic substitution x a cosh t can also be used. Using the identity cosh2 y sinh2 y 1, we have
sx 2 a 2 sa 2 cosh2 t 1 sa 2 sinh2 t a sinh t
Since dx a sinh t dt, we obtain
|
y |
|
dx |
y |
a sinh t dt |
ydt t C |
|||||||
|
s |
|
|
a sinh t |
|||||||||
|
x 2 a 2 |
||||||||||||
Since cosh t x a, we have t cosh 1 x a and |
|||||||||||||
2 |
|
|
y |
|
dx |
cosh 1 |
x |
C |
|||||
s |
|
|
|
|
a |
||||||||
x 2 a 2 |
|||||||||||||

SECTION 7.3 TRIGONOMETRIC SUBSTITUTION |||| |
471 |
Although Formulas 1 and 2 look quite different, they are actually equivalent by |
|
Formula 3.11.4. |
M |
NOTE As Example 5 illustrates, hyperbolic substitutions can be used in place of trigonometric substitutions and sometimes they lead to simpler answers. But we usually use trigonometric substitutions because trigonometric identities are more familiar than hyperbolic identities.
3 |
s |
3 2 |
|
x 3 |
|
|
|||||
EXAMPLE 6 Find y0 |
|
|
|
dx. |
|
|
|||||
|
|
|
4x 2 9 3 2 |
|
|
||||||
SOLUTION First we note that 4x |
2 9 3 2 |
|
|
)3 so trigonometric substitution |
|||||||
4x 2 |
9 |
||||||||||
is appropriate. Although |
|
|
|
|
s |
|
|
||||
|
4x 2 |
9 |
is not quite one of the expressions in the table of |
||||||||
|
|
|
|
s |
|
|
|
|
|
|
|
trigonometric substitutions, it becomes one of them if we make the preliminary substitution u 2x. When we combine this with the tangent substitution, we have x 32 tan , which gives dx 32 sec2 d and
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
4x 2 9 |
9 tan2 |
9 3 sec |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
When x 0, tan 0, so |
0; when x 3s |
|
2, tan s |
|
, so |
|
|
3. |
|
|||||||||||||||||||||||||||||||||||||||||
3 |
3 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
27 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
s |
3 2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
tan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
y0 |
|
|
|
|
dx y0 |
|
|
|
|
23 sec2 d |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
4x 2 9 3 2 |
27 |
sec3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 tan |
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
d |
|
y0 |
|
|
|
d |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
sec |
|
16 |
|
cos2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 1 cos2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
sin d |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
cos2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Now we substitute u cos |
so that du sin |
d . When |
0, u 1; when |
|
||||||||||||||||||||||||||||||||||||||||||||||
3, u 21. Therefore |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 |
|
2 |
|
|
x 3 |
|
|
|
|
|
|
|
|
|
1 2 1 u 2 |
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
y0 s |
|
|
|
|
|
|
|
dx |
y1 |
|
|
|
|
|
|
|
|
|
du |
y1 |
1 |
u 2 |
du |
|
||||||||||||||||||||||||||
|
|
4x 2 9 3 2 |
16 |
|
|
|
|
u 2 |
|
|
|
16 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
u |
1 |
1 |
|
|
3 |
|
[(21 2) 1 1 ] |
3 |
|
M |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
16 |
|
u |
|
16 |
32 |
||||||||||||||||||||||||||||||||||
EXAMPLE 7 Evaluate y |
|
|
|
x |
|
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 2x x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
SOLUTION We can transform the integrand into a function for which trigonometric substitution is appropriate by first completing the square under the root sign:
32x x 2 3 x 2 2x 3 1 x 2 2x 1
4 x 1 2
This suggests that we make the substitution u x 1. Then du dx and x u 1, so
|
|
x |
u 1 |
|||||
y |
|
|
|
dx y |
|
|
|
du |
|
s |
|
|
|||||
|
3 2x x 2 |
|
4 u 2 |
|||||
|
s |
|
|
|
||||
472 |||| CHAPTER 7 TECHNIQUES OF INTEGRATION
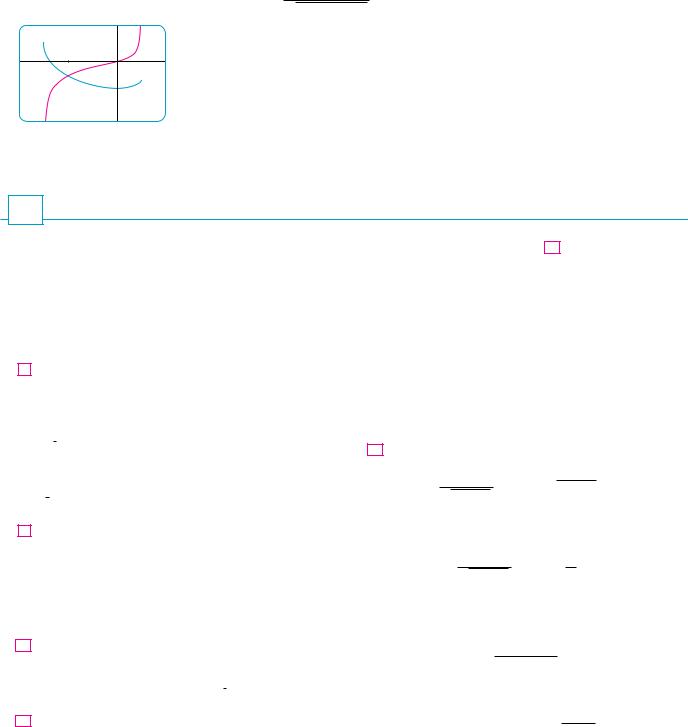
N Figure 5 shows the graphs of the integrand in Example 7 and its indefinite integral (with C 0). Which is which?
3
_4 |
2 |
_5
FIGURE 5
7.3EXERCISES
We now substitute u
y s3
x
2x
2sin
x2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, giving du 2 cos d and s4 u2 |
|
|||||||||||||||
dx y |
2 sin |
1 |
2 cos d |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||
|
2 cos |
|
|
|
|
|
||||||||||
y 2 sin |
1 d |
|
|
|
|
|
|
|
|
|||||||
2 cos |
C |
|
2 |
|
|
|
|
|||||||||
|
s |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
4 |
u2 |
|
sin 1 |
|
|
u |
C |
|
|
|||||
|
|
|
|
|
|
|
||||||||||
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
3 |
2x |
x2 |
sin 1 |
|
x |
|
||||||||
|
|
|
|
|
||||||||||||
2 cos , so
C |
M |
1–3 Evaluate the integral using the indicated trigonometric substitution. Sketch and label the associated right triangle.
1. |
y |
1 |
|
|
dx; |
x 3 sec |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x 2 s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
x 2 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2. |
yx 3 s |
|
|
|
dx; |
x 3 sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3. |
y |
x |
|
dx; x 3 tan |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
x 2 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4 –30 Evaluate the integral. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
2 |
s |
3 |
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. |
y0 |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
16 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
s |
x 2 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. |
ys2 |
|
|
|
|
|
|
|
|
dt |
|
6. |
y1 |
|
|
|
|
|
|
dx |
|||||||||||||||||||||||||||||||
t 3 s |
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
t 2 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
7. |
y |
|
|
|
|
|
|
|
dx |
|
8. |
y |
|
|
x |
|
|
|
|
dx |
|||||||||||||||||||||||||||||||
x 2 s |
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
25 |
x 2 |
|
|
x 2 |
100 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9. |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
y |
|
|
|
t |
|
dt |
|||||||||||||||||||||||||||
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
||||||||||||||||||||||||||||
x 2 16 |
|
|
|
|
|
|
|
|
|
|
|
|
t 2 2 |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
ys1 4x 2 dx |
|
12. |
y0 x sx 2 4 dx |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
13. |
y |
sx 9 |
|
dx |
|
14. |
y |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
x 3 |
|
u s |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
5 u 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3 |
|
|
dx |
|||||||||||||||||
15. |
y0 |
x 2sa 2 x 2 dx |
|
16. |
ys2 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
x 5s |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
9x 2 1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
17. |
y |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
dx |
|
18. |
y |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
s |
|
|
|
|
|
|
|
|
ax 2 b 2 3 2 |
|||||||||||||||||||||||||||||||||||||||||
|
x 2 7 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
y |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
||||||||||
19. |
1 |
x 2 |
|
|
|
dx |
|
20. |
y |
|
|
|
|
|
|
|
|
dt |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
25 t 2 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
0.6 |
|
|
x 2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
21. |
y0 |
|
|
|
|
|
dx |
22. |
y0 |
sx 2 1 dx |
|||||||||||||||
|
s |
|
|
|
|||||||||||||||||||||
|
9 25x 2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|||||||
23. |
ys5 4x x 2 dx |
24. |
y |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
s |
|
|
|
|
||||||||||||||||||||
|
t 2 6t 13 |
|
|
||||||||||||||||||||||
25. |
y |
|
|
|
x |
|
|
|
26. |
y |
|
|
|
|
x 2 |
||||||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
dx |
|||||||||||
s |
|
|
|
|
|
3 4x 4x 2 3 2 |
|||||||||||||||||||
x 2 x 1 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 1 |
||||||||
27. |
ysx 2 2x dx |
|
|
|
28. |
y |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|||||||||||||||
|
|
|
|
x 2 2x 2 2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos t |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
29. |
yx s1 x 4 dx |
|
|
|
30. |
y0 |
|
|
|
|
|
|
dt |
||||||||||||
|
|
|
|
|
s |
|
|
|
|||||||||||||||||
|
|
|
|
|
1 sin2t |
||||||||||||||||||||
31. (a) Use trigonometric substitution to show that
ysx 2dx a 2 ln(x sx 2 a 2 ) C
(b)Use the hyperbolic substitution x a sinh t to show that
y sx 2dx a 2 sinh 1 ax C
These formulas are connected by Formula 3.11.3.
32. Evaluate
x 2
yx 2 a 2 3 2 dx
(a)by trigonometric substitution.
(b)by the hyperbolic substitution x a sinh t.
33.Find the average value of f x sx 2 1 x , 1 x 7.
34.Find the area of the region bounded by the hyperbola 9x 2 4y 2 36 and the line x 3.
