
- •CONTENTS
- •Preface
- •To the Student
- •Diagnostic Tests
- •1.1 Four Ways to Represent a Function
- •1.2 Mathematical Models: A Catalog of Essential Functions
- •1.3 New Functions from Old Functions
- •1.4 Graphing Calculators and Computers
- •1.6 Inverse Functions and Logarithms
- •Review
- •2.1 The Tangent and Velocity Problems
- •2.2 The Limit of a Function
- •2.3 Calculating Limits Using the Limit Laws
- •2.4 The Precise Definition of a Limit
- •2.5 Continuity
- •2.6 Limits at Infinity; Horizontal Asymptotes
- •2.7 Derivatives and Rates of Change
- •Review
- •3.2 The Product and Quotient Rules
- •3.3 Derivatives of Trigonometric Functions
- •3.4 The Chain Rule
- •3.5 Implicit Differentiation
- •3.6 Derivatives of Logarithmic Functions
- •3.7 Rates of Change in the Natural and Social Sciences
- •3.8 Exponential Growth and Decay
- •3.9 Related Rates
- •3.10 Linear Approximations and Differentials
- •3.11 Hyperbolic Functions
- •Review
- •4.1 Maximum and Minimum Values
- •4.2 The Mean Value Theorem
- •4.3 How Derivatives Affect the Shape of a Graph
- •4.5 Summary of Curve Sketching
- •4.7 Optimization Problems
- •Review
- •5 INTEGRALS
- •5.1 Areas and Distances
- •5.2 The Definite Integral
- •5.3 The Fundamental Theorem of Calculus
- •5.4 Indefinite Integrals and the Net Change Theorem
- •5.5 The Substitution Rule
- •6.1 Areas between Curves
- •6.2 Volumes
- •6.3 Volumes by Cylindrical Shells
- •6.4 Work
- •6.5 Average Value of a Function
- •Review
- •7.1 Integration by Parts
- •7.2 Trigonometric Integrals
- •7.3 Trigonometric Substitution
- •7.4 Integration of Rational Functions by Partial Fractions
- •7.5 Strategy for Integration
- •7.6 Integration Using Tables and Computer Algebra Systems
- •7.7 Approximate Integration
- •7.8 Improper Integrals
- •Review
- •8.1 Arc Length
- •8.2 Area of a Surface of Revolution
- •8.3 Applications to Physics and Engineering
- •8.4 Applications to Economics and Biology
- •8.5 Probability
- •Review
- •9.1 Modeling with Differential Equations
- •9.2 Direction Fields and Euler’s Method
- •9.3 Separable Equations
- •9.4 Models for Population Growth
- •9.5 Linear Equations
- •9.6 Predator-Prey Systems
- •Review
- •10.1 Curves Defined by Parametric Equations
- •10.2 Calculus with Parametric Curves
- •10.3 Polar Coordinates
- •10.4 Areas and Lengths in Polar Coordinates
- •10.5 Conic Sections
- •10.6 Conic Sections in Polar Coordinates
- •Review
- •11.1 Sequences
- •11.2 Series
- •11.3 The Integral Test and Estimates of Sums
- •11.4 The Comparison Tests
- •11.5 Alternating Series
- •11.6 Absolute Convergence and the Ratio and Root Tests
- •11.7 Strategy for Testing Series
- •11.8 Power Series
- •11.9 Representations of Functions as Power Series
- •11.10 Taylor and Maclaurin Series
- •11.11 Applications of Taylor Polynomials
- •Review
- •APPENDIXES
- •A Numbers, Inequalities, and Absolute Values
- •B Coordinate Geometry and Lines
- •E Sigma Notation
- •F Proofs of Theorems
- •G The Logarithm Defined as an Integral
- •INDEX

cream cone, as shown in the figure. If |
A! |
$ |
" is the area of the |
|||||||
semicircle and B! |
$ |
" |
is the area of the triangle, find |
|||||||
|
|
|
lim A! |
$ |
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
$l0! |
B!$" |
|
|
|
|
||
|
|
|
A(¬) |
|
|
|
|
|
|
|
|
P |
B(¬) |
|
|
|
Q |
|
|||
|
|
|
|
|
|
|
|
|
||
|
10 cm |
|
|
10 cm |
|
|||||
|
|
|
¬ |
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
SECTION 3.4 THE CHAIN RULE |||| 197
51. The figure shows a circular arc of length s and a chord of length d, both subtended by a central angle $. Find
lim s
$l0! d
d s
¬
N See Section 1.3 for a review of composite functions.
3.4THE CHAIN RULE
Suppose you are asked to differentiate the function
F!x" ! sx2 ! 1
The differentiation formulas you learned in the previous sections of this chapter do not enable you to calculate F#!x".
Observe that F is a composite function. In fact, if we let y ! f !u" ! su and let u ! t!x" ! x2 ! 1, then we can write y ! F!x" ! f ! t!x"", that is, F ! f ! t. We know how to differentiate both f and t, so it would be useful to have a rule that tells us how to find the derivative of F ! f ! t in terms of the derivatives of f and t.
It turns out that the derivative of the composite function f ! tis the product of the derivatives of f and t. This fact is one of the most important of the differentiation rules and is called the Chain Rule. It seems plausible if we interpret derivatives as rates of change. Regard du%dx as the rate of change of u with respect to x, dy%du as the rate of change of y with respect to u, and dy%dx as the rate of change of y with respect to x. If u changes twice as fast as x and y changes three times as fast as u, then it seems reasonable that y changes six times as fast as x, and so we expect that
dy |
dy |
du |
dx |
! du |
dx |
THE CHAIN RULE If t is differentiable at x and f is differentiable at t!x", then the composite function F ! f ! t defined by F!x" ! f ! t!x"" is differentiable at x and F#is given by the product
F#!x" ! f #! t!x"" ! t#!x"
In Leibniz notation, if y ! f !u" and u ! t!x" are both differentiable functions, then
dy |
dy |
du |
dx |
! du |
dx |

198 |||| CHAPTER 3 DIFFERENTIATION RULES
COMMENTS ON THE PROOF OF THE CHAIN RULE Let +u be the change in u corresponding to a change of +x in x, that is,
+u ! t!x ! +x" " t!x"
Then the corresponding change in y is
+y ! f !u ! +u" " f !u"
It is tempting to write
dy |
! lim |
+y |
|
dx |
+x |
||
+x l0 |
1! lim +y ! +u
+x l0 +u +x
!lim +y ! lim +u
+x l0 +u +x l0 +x
! lim |
|
+y |
! lim |
+u |
(Note that +u l 0 as +x l 0 |
|
since t is continuous.) |
||||
|
|
+x |
|||
+u l0 +u |
+x l0 |
|
|||
dy |
du |
|
|
|
|
! du |
dx |
|
|
|
|
The only flaw in this reasoning is that in (1) it might happen that +u ! 0 (even when +x " 0) and, of course, we can’t divide by 0. Nonetheless, this reasoning does at least suggest that the Chain Rule is true. A full proof of the Chain Rule is given at the end of
this section. |
|
|
M |
The Chain Rule can be written either in the prime notation |
|||
2 |
! f ! t"#!x" ! f #! t!x"" ! t#!x" |
||
or, if y ! f !u" and u ! t!x", in Leibniz notation: |
|||
|
dy |
dy |
du |
3 |
dx |
! du |
dx |
Equation 3 is easy to remember because if dy%du and du%dx were quotients, then we could cancel du. Remember, however, that du has not been defined and du%dx should not be thought of as an actual quotient.
EXAMPLE 1 Find F#!x" if F!x" ! sx2 ! 1.
SOLUTION 1 (using Equation 2): At the beginning of this section we expressed F as
F!x" ! ! f ! t"!x" ! f ! t!x"" where f !u" ! su and t!x" ! x2 ! 1. Since
|
f #!u" ! 21 u"1%2 ! |
1 |
|
|
|
|
and |
||
|
|
|
|
|
|
|
|||
|
|
2su |
|||||||
|
|
|
|
|
|||||
we have |
F#!x" ! f #! t!x"" ! t#!x" |
||||||||
|
! |
|
1 |
|
|
|
|
! 2x ! |
|
|
|
|
|
|
|
|
|||
|
2s |
|
|
|
|
|
|
||
|
x2 ! 1 |
||||||||
t#!x" ! 2x
x
sx2 ! 1

|
|
|
|
|
SECTION 3.4 THE CHAIN RULE |||| |
199 |
|||||||||
SOLUTION 2 (using Equation 3): If we let u ! x2 ! 1 and y ! s |
|
, then |
|
||||||||||||
u |
|
||||||||||||||
|
dy du |
1 |
|
|
|
|
|
|
|
|
|
|
|||
F#!x" ! du dx ! |
|
|
|
|
!2x" |
|
|||||||||
|
2s |
|
|
|
|||||||||||
|
u |
|
|
||||||||||||
1 |
|
|
!2x" |
|
|
|
x |
|
|||||||
! |
|
|
|
|
! |
|
|
|
|
|
|
M |
|||
2s |
|
|
|
s |
|
|
|||||||||
x2 ! 1 |
x2 ! 1 |
||||||||||||||
When using Formula 3 we should bear in mind that dy%dx refers to the derivative of y when y is considered as a function of x (called the derivative of y with respect to x), whereas dy%du refers to the derivative of y when considered as a function of u (the derivative of y with respect to u). For instance, in Example 1, y can be considered as a function of x (y ! sx2 ! 1) and also as a function of u (y ! su ). Note that
dy |
! F#!x" ! |
|
x |
whereas |
dy |
! f #!u" ! |
1 |
|
|
|
dx |
s |
|
|
du |
2s |
|
|
|||
x2 ! 1 |
u |
|||||||||
NOTE In using the Chain Rule we work from the outside to the inside. Formula 2 says that we differentiate the outer function f [at the inner function t!x"] and then we multiply by the derivative of the inner function.
d |
f |
! t!x"" |
! f # |
! t!x"" |
! |
t#!x" |
|
dx |
|||||||
|
|
|
|
|
|
||
|
outer |
evaluated |
derivative |
evaluated |
|
derivative |
|
|
function |
at inner |
of outer |
at inner |
|
of inner |
|
|
|
function |
function |
function |
|
function |
V EXAMPLE 2 Differentiate (a) y ! sin!x2 " and (b) y ! sin2x.
SOLUTION
(a) If y ! sin!x2 ", then the outer function is the sine function and the inner function is the squaring function, so the Chain Rule gives
dy |
! |
d |
sin |
!x2 " |
! |
cos |
!x2 " |
! |
2x |
|
dx |
dx |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
outer |
evaluated |
|
derivative |
evaluated |
|
derivative |
|
|
|
|
function |
at inner |
|
of outer |
at inner |
|
of inner |
|
|
! 2x cos!x2 " |
function |
|
function |
function |
|
function |
|||
|
|
|
|
|
|
|
||||
(b) Note that sin2x ! !sin x"2. Here the outer function is the squaring function and the inner function is the sine function. So
dy |
! |
d |
!sin x"2 |
! |
2 |
! |
!sin x" |
! |
cos x |
|
dx |
dx |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
|
inner |
|
derivative |
evaluated |
|
derivative |
||
|
|
|
function |
|
of outer |
at inner |
|
of inner |
||
|
|
|
|
|
function |
function |
|
function |
||
N See Reference Page 2 or Appendix D.
The answer can be left as 2 sin x cos x or written as sin 2x (by a trigonometric identity |
|
known as the double-angle formula). |
M |
In Example 2(a) we combined the Chain Rule with the rule for differentiating the sine function. In general, if y ! sin u, where u is a differentiable function of x, then, by the Chain Rule,
dydx ! dudy dudx ! cos u dudx

200 |||| CHAPTER 3 DIFFERENTIATION RULES |
|
|
|
|
Thus |
d |
!sin u" ! cos u |
du |
|
dx |
dx |
|||
|
|
In a similar fashion, all of the formulas for differentiating trigonometric functions can be combined with the Chain Rule.
Let’s make explicit the special case of the Chain Rule where the outer function f is a power function. If y ! ' t!x"(n, then we can write y ! f !u" ! un where u ! t!x". By using the Chain Rule and then the Power Rule, we get
dydx ! dudy dudx ! nun"1 dudx ! n' t!x"(n"1t#!x"
4 THE POWER RULE COMBINED WITH THE CHAIN RULE If n is any real number |
|||||
and u ! t!x" is differentiable, then |
|
||||
|
|
|
d |
|
!un " ! nun"1 du |
|
|
|
dx |
||
|
|
|
dx |
||
Alternatively, |
d |
' t!x"(n ! n' t!x"(n"1 ! t#!x" |
|||
dx |
|||||
Notice that the derivative in Example 1 could be calculated by taking n ! 12 in Rule 4.
EXAMPLE 3 Differentiate y ! !x3 " 1"100.
SOLUTION Taking u ! t!x" ! x3 " 1 and n ! 100 in (4), we have
|
dy |
! |
d |
!x3 |
" 1"100 ! 100!x3 " 1"99 |
d |
|
!x3 " 1" |
|
||||||||||||||||||
|
dx |
|
dx |
|
|||||||||||||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
! 100!x3 " 1"99 ! 3x2 ! 300x2!x3 " 1"99 |
M |
||||||||||||||||||||||||
|
EXAMPLE 4 Find f #!x" if f !x" |
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
V |
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
sx2 ! x ! 1 |
|
|
|
|
|
|
|
|
|
|||||
SOLUTION First rewrite f : |
|
|
f !x" ! !x2 ! x ! 1""1%3 |
|
|
|
|
|
|
||||||||||||||||||
Thus |
f #!x" ! "31 !x2 ! x ! 1""4%3 |
d |
!x2 |
! x ! 1" |
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
||
|
|
|
|
|
! "31 !x2 ! x ! 1""4%3!2x ! 1" |
|
|
M |
|||||||||||||||||||
EXAMPLE 5 Find the derivative of the function |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t!t" ! # |
t " 2 |
$9 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2t ! 1 |
|
|
|
|
|
|
||||||||||
SOLUTION Combining the Power Rule, Chain Rule, and Quotient Rule, we get |
|
||||||||||||||||||||||||||
|
t#!t" ! 9# |
t " 2 |
|
$8 |
|
|
d |
# |
t " 2 |
$ |
|
|
|
|
|
|
|
|
|
|
|||||||
2t ! 1 |
|
|
dt |
2t ! 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
t " 2 |
8 |
|
|
!2t ! 1" ! 1 " 2!t " 2" |
|
|
|
45!t " 2"8 |
|
||||||||||||||
! 9# |
|
|
|
|
$ |
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
M |
|||||
|
2t ! 1 |
|
|
|
|
|
|
!2t ! 1"2 |
|
|
|
!2t ! 1"10 |
|
||||||||||||||
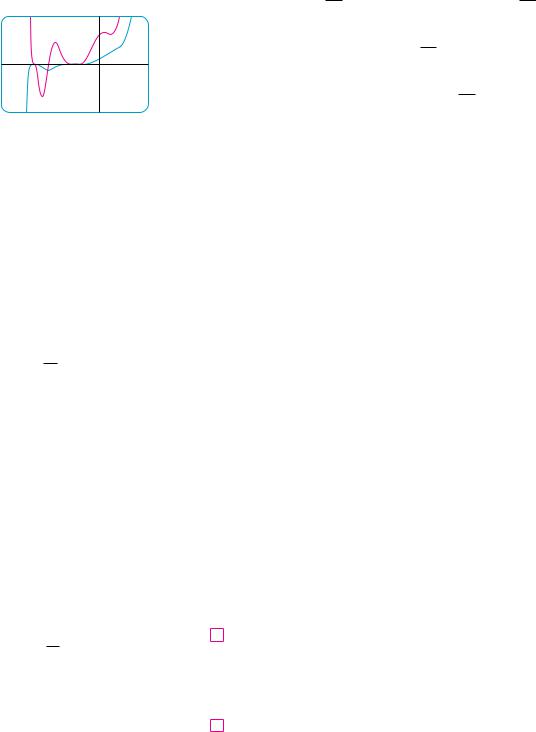
N The graphs of the functions y and y# in Example 6 are shown in Figure 1. Notice that
y# is large when y increases rapidly and y# ! 0 when y has a horizontal tangent. So our answer appears to be reasonable.
10
y»
_2 |
1 |
y
_10
FIGURE 1
N More generally, the Chain Rule gives dxd !eu" ! eu dudx
N Don’t confuse Formula 5 (where x is the exponent) with the Power Rule (where x is the base):
dxd !x n " ! nx n"1
SECTION 3.4 THE CHAIN RULE |||| 201
EXAMPLE 6 Differentiate y ! !2x ! 1"5!x3 " x ! 1"4.
SOLUTION In this example we must use the Product Rule before using the Chain Rule: dydx ! !2x ! 1"5 dxd !x3 " x ! 1"4 ! !x3 " x ! 1"4 dxd !2x ! 1"5
!!2x ! 1"5 ! 4!x3 " x ! 1"3 dxd !x3 " x ! 1"
!!x3 " x ! 1"4 ! 5!2x ! 1"4 dxd !2x ! 1"
!4!2x ! 1"5!x3 " x ! 1"3!3x2 " 1" ! 5!x3 " x ! 1"4!2x ! 1"4 ! 2
Noticing that each term has the common factor 2!2x ! 1"4!x3 " x ! 1"3, we could factor it out and write the answer as
dydx ! 2!2x ! 1"4!x3 " x ! 1"3!17x3 ! 6x2 " 9x ! 3" M
EXAMPLE 7 Differentiate y ! esin x.
SOLUTION Here the inner function is t!x" ! sin x and the outer function is the exponential function f !x" ! ex. So, by the Chain Rule,
dy |
! |
d |
!esin x " ! esin x |
d |
!sin x" ! esin x cos x |
M |
|
dx |
dx |
dx |
|||||
|
|
|
|
We can use the Chain Rule to differentiate an exponential function with any base a - 0. Recall from Section 1.6 that a ! eln a. So
|
|
|
|
ax ! !eln a "x ! e!ln a" x |
|
|
|||||
and the Chain Rule gives |
|
|
|
|
|
|
|
|
|
|
|
|
d |
!ax " ! |
|
|
d |
|
!e!ln a" x " ! e!ln a" x |
d |
!ln a"x |
||
|
dx |
|
dx |
dx |
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
! e!ln a" x , ln a ! ax ln a |
|
|
||||||
because ln a is a constant. So we have the formula |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
5 |
|
|
|
|
|
d |
!ax " ! ax ln a |
|
|
||
|
|
|
|
dx |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
In particular, if a ! 2, we get |
|
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
|
d |
!2x " ! 2x ln 2 |
|
|
||
|
|
|
|
dx |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||

202 |||| CHAPTER 3 DIFFERENTIATION RULES
In Section 3.1 we gave the estimate
dxd "2x # ' "0.69#2x
This is consistent with the exact formula (6) because ln 2 ' 0.693147.
The reason for the name “Chain Rule” becomes clear when we make a longer chain by adding another link. Suppose that y ! f "u#, u ! t" x#, and x ! h"t#, where f , t, and h are differentiable functions. Then, to compute the derivative of y with respect to t, we use the Chain Rule twice:
|
dy |
dy |
dx |
|
dy |
du |
|
dx |
|
|
|
|
|
|
! dx |
|
! du |
|
|
|
|
|
|
||
|
dt |
dt |
dx |
|
dt |
|
|
|
||||
|
EXAMPLE 8 If f " x# ! sin"cos"tan x##, then |
|
|
|
|
|
|
|
||||
V |
|
|
|
|
|
|
|
|||||
|
f $" x# ! cos"cos"tan x## |
d |
cos"tan x# |
|
|
|
||||||
|
|
|
|
|||||||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
! cos"cos"tan x## %#sin"tan x#& |
|
d |
|
"tan x# |
|||||||
|
dx |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
! #cos"cos"tan x## sin"tan x# sec2x |
|
||||||||||
Notice that we used the Chain Rule twice. |
|
|
|
|
|
|
|
|
M |
|||
|
|
& |
|
|
|
|
|
|
|
|
|
|
EXAMPLE 9 Differentiate y ! esec 3 . |
|
|
|
|
|
|
|
|
|
|
||
SOLUTION The outer function is the exponential function, the middle function is the secant function and the inner function is the tripling function. So we have
dy |
! esec 3 |
& |
d |
"sec 3&# |
|
|
d& |
|
|
|
|
||
|
|
d& |
|
|
||
|
! esec 3 |
& sec 3& tan 3& |
d |
"3 |
||
|
d& |
|||||
|
|
|
|
|
|
|
|
! 3esec 3 |
& sec 3& tan 3& |
M |
|||
HOW TO PROVE THE CHAIN RULE
Recall that if y ! f " x# and x changes from a to a % !x, we defined the increment of y as
!y ! f "a % !x# # f "a#
According to the definition of a derivative, we have
lim |
!y |
! f $"a# |
|
!x |
|||
!x l0 |
|
So if we denote by " the difference between the difference quotient and the derivative, we obtain
lim " ! lim |
!y |
# f $"a# |
$ |
! f $"a# # f $"a# ! 0 |
|
!x |
|||||
!x l0 !x l0! |
|
|

|
|
|
SECTION 3.4 THE CHAIN RULE |||| 203 |
|
But |
|
y |
f a ? y f a x x |
|
x |
||||
|
|
|
If we define to be 0 when x 0, then becomes a continuous function of x. Thus, for a differentiable function f, we can write
7 |
y f a x x where l 0 as x l 0 |
and is a continuous function of x. This property of differentiable functions is what enables us to prove the Chain Rule.
PROOF OF THE CHAIN RULE Suppose u t x is differentiable at a and y f u is differentiable at b t a . If x is an increment in x and u and y are the corresponding increments in u and y, then we can use Equation 7 to write
8 |
u t a x 1 x t a 1 x |
where 1 l 0 as x l 0. Similarly
9 |
y f b u 2 u f b 2 u |
where 2 l 0 as u l 0. If we now substitute the expression for u from Equation 8 into Equation 9, we get
|
y f b 2 t a 1 x |
||
so |
|
y |
f b 2 t a 1 |
|
|
||
|
x |
||
As x l 0, Equation 8 shows that u l 0. So both 1 l 0 and 2 l 0 as x l 0. Therefore
dy |
lim |
y |
lim f b 2 t a 1 |
|
dx |
x |
|||
x l0 |
x l0 |
f b t a f t a t a
This proves the Chain Rule.
M
3.4E X E R C I S E S
1–6 Write the composite function in the form f t x . [Identify the inner function u t x and the outer function y f u .] Then find the derivative dy dx .
|
|
|
|
|
|
1. |
y sin 4x |
2. |
y s4 3x |
||
3. |
y 1 x 2 10 |
4. |
y tan sin x |
||
5. |
y esx |
6. |
y sin e x |
||
|
|
|
|||
7– 46 Find the derivative of the function. |
|||||
7. |
F x x 4 3x 2 2 5 |
8. |
F x 4 x x 2 100 |
||
9. |
F x 4 |
1 2x x 3 |
||
|
|
s |
|
|
11. |
t t |
|
1 |
|
|
|
|
||
t 4 1 3 |
||||
13. |
y cos a3 x 3 |
|||
15. |
y xe kx |
|
|
|
17.t x 1 4x 5 3 x x2 8
18.h t t 4 1 3 t 3 1 4
19.y 2x 5 4 8x 2 5 3
10.f x 1 x 4 2 3
12.f t s3 1 tan t
14.y a3 cos3x
16.y 3 cot n
20.y x 2 1 s3 x 2 2
204 |||| CHAPTER 3 DIFFERENTIATION RULES
!x2 % 1 $3
21. y ! x2 # 1
23. y ! ex cos x
25. F"z# !
*z # 1
z % 1
r
27. y ! sr2 % 1
29. y ! sin"tan 2x#
31. y ! 2sin |
( |
x |
|
33. y ! sec2x % tan2x
!1 # e2x $
35.y ! cos 1 % e2x
37.y ! cot2"sin
39.f " t# ! tan"et # % etan t
41. |
f " t# ! sin2"esin2 t # |
||
43. |
t" x# ! "2rarx % n# p |
||
45. |
y ! coss |
|
|
sin"tan (x# |
|||
22. |
y ! e#5x cos 3x |
|||||||||||||||
24. |
y ! 101#x 2 |
|
|
|
|
|
|
|
|
|
||||||
26. |
G" y# ! |
" y # 1# 4 |
||||||||||||||
" y2 % 2y# 5 |
|
|||||||||||||||
28. |
y ! |
eu # e#u |
|
|
|
|
|
|
||||||||
eu % e#u |
|
|
|
|
|
|
|
|||||||||
30. |
G" y# ! ! |
y2 |
|
$5 |
|
|
|
|||||||||
y % |
1 |
|
|
|
||||||||||||
32. |
y ! tan2"3 |
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
34. |
y ! x sin |
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36. |
f " t# ! |
|
|
|
|
|
|
t |
|
|
|
|
|
|
||
*t |
2 % 4 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
38. |
y ! ek tan sx |
|
|
|
|
|
|
|
|
|
||||||
40. |
y ! sin"sin"sin x## |
|||||||||||||||
|
y ! s |
|
|
|
|
|
|
|
|
|
|
|
|
|||
42. |
x % s |
|
|
|
|
|
|
|
|
|||||||
x % s |
|
|
|
|||||||||||||
x |
||||||||||||||||
44. |
y ! 23x2 |
|
|
|
|
|
|
|
|
|
||||||
46. |
y ! %x % " x % sin2x#3& 4 |
|||||||||||||||
47–50 Find the first and second derivatives of the function.
47. |
h" x# ! s |
|
48. |
y ! xecx |
x2 % 1 |
||||
49. |
y ! e )x sin *x |
50. |
y ! ee x |
|
;58. The function f " x# ! sin" x % sin 2x#, 0 ' x ' (, arises in applications to frequency modulation (FM) synthesis.
(a)Use a graph of f produced by a graphing device to make a rough sketch of the graph of f $.
(b)Calculate f $" x# and use this expression, with a graphing device, to graph f $. Compare with your sketch in part (a).
59.Find all points on the graph of the function
f " x# ! 2 sin x % sin2x at which the tangent line is horizontal. 60. Find the x-coordinates of all points on the curve
|
y ! sin 2x # 2 sin x at which the tangent line is horizontal. |
||||||||||
|
If F" x# ! f " t" x##, where f "#2# ! 8, f $"#2# ! 4, f $"5# ! 3, |
||||||||||
61. |
|||||||||||
|
t"5# ! #2, and t$"5# ! 6, find F$"5#. |
|
|
||||||||
62. |
If h" x# ! s |
|
|
, where f "1# ! 7 and f $"1# ! 4, |
|||||||
4 % 3f " x# |
|||||||||||
|
find h$"1#. |
|
|
|
|
|
|
|
|
||
63. |
A table of values for f , t, f $, and t$ is given. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
f " x# |
t" x# |
f $" x# |
|
t$" x# |
|
|
|
|
1 |
|
3 |
|
2 |
4 |
|
6 |
|
|
|
|
2 |
|
1 |
|
8 |
5 |
|
7 |
|
|
|
|
3 |
|
7 |
|
2 |
7 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
(a) If h" x# ! f " t" x##, find h$"1#. |
|
|
|
|
||||||
|
(b) If H" x# ! t" f " x##, find H$"1#. |
|
|
|
|
||||||
64. |
Let f and t be the functions in Exercise 63. |
|
|
||||||||
|
(a) If F" x# ! f " f " x##, find F$"2#. |
|
|
|
|
||||||
|
(b) If G" x# ! t" t" x##, find G$"3#. |
|
|
|
|
||||||
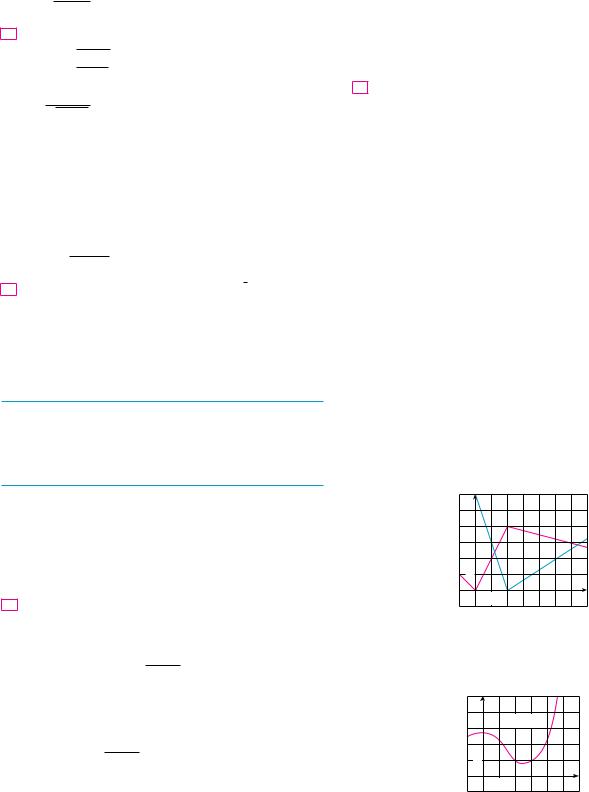
|
If f and t are the functions whose graphs are shown, let |
||||||||||
65. |
|||||||||||
|
u" x# ! f " t" x##, v" x# ! t" f " x##, and w" x# ! t" t" x##. Find |
||||||||||
|
each derivative, if it exists. If it does not exist, explain why. |
||||||||||
|
(a) u$"1# |
(b) v$"1# |
(c) w$"1# |
|
|
||||||
51–54 Find an equation of the tangent line to the curve at the given point.
51. |
y ! "1 % 2x#10, |
"0, 1# |
52. |
y ! sin x % sin2x, "0, 0# |
53. |
y ! sin"sin x#, |
"(, 0# |
54. |
y ! x2e#x, "1, 1(e# |
|
|
|
|
|
55.(a) Find an equation of the tangent line to the curve y ! 2("1 % e#x # at the point "0, 1#.
;(b) Illustrate part (a) by graphing the curve and the tangent line on the same screen.
56.(a) The curve y ! ) x )(s2 # x2 is called a bullet-nose curve. Find an equation of the tangent line to this curve at the point "1, 1#.
;(b) Illustrate part (a) by graphing the curve and the tangent line on the same screen.
57.(a) If f " x# ! xs2 # x2 , find f $" x#.
;(b) Check to see that your answer to part (a) is reasonable by
comparing the graphs of f and f $.
y |
|
|
|
|
f |
1 |
|
g |
|
|
|
0 |
1 |
x |
66. If f is the function whose graph is shown, let h" x# ! f " f " x## and t" x# ! f " x2 #. Use the graph of f to estimate the value of each derivative.
(a) h$"2# (b) t$"2#
y |
|
|
|
|
y=Ä |
1 |
|
|
0 |
1 |
x |

67.Suppose f is differentiable on !. Let F" x# ! f "ex # and G" x# ! e f " x#. Find expressions for (a) F$" x# and (b) G$" x#.
68. Suppose |
f is differentiable on ! and ) is a real number. |
|||
Let F" x# |
! f " x |
) |
# and G" x# ! % f " x#& |
) |
|
. Find expressions |
|||
for (a) F$" x# and (b) G$" x#.
69.Let r" x# ! f " t"h" x###, where h"1# ! 2, t"2# ! 3, h$"1# ! 4, t$"2# ! 5, and f $"3# ! 6. Find r$"1#.
70. If t is a twice differentiable function and f " x# ! xt" x2 #, find f 0 in terms of t, t$, and t0.
71.If F" x# ! f "3f "4 f " x###, where f "0# ! 0 and f $"0# ! 2, find F$"0#.
72.If F" x# ! f " x f " x f " x###, where f "1# ! 2, f "2# ! 3, f $"1# ! 4, f $"2# ! 5, and f $"3# ! 6, find F$"1#.
73.Show that the function y ! Ae#x % Bxe#x satisfies the differential equation y0 % 2y$ % y ! 0.
74.For what values of r does the function y ! erx satisfy the equation y0 % 5y$ # 6y ! 0?
75.Find the 50th derivative of y ! cos 2x.
76.Find the 1000th derivative of f" x# ! xe#x.
77.The displacement of a particle on a vibrating string is given by the equation
s"t# ! 10 % 14 sin"10(t#
where s is measured in centimeters and t in seconds. Find the velocity of the particle after t seconds.
78. If the equation of motion of a particle is given by
s ! A cos".t % /#, the particle is said to undergo simple harmonic motion.
(a) Find the velocity of the particle at time t.
(b) When is the velocity 0?
79. A Cepheid variable star is a star whose brightness alternately increases and decreases. The most easily visible such star is Delta Cephei, for which the interval between times of maximum brightness is 5.4 days. The average brightness of this star is 4.0 and its brightness changes by -0.35. In view of these data, the brightness of Delta Cephei at time t, where t is measured in days, has been modeled by the function
B"t# ! 4.0 % 0.35 sin!2(t $ 5.4
(a) Find the rate of change of the brightness after t days.
(b) Find, correct to two decimal places, the rate of increase after one day.
80. In Example 4 in Section 1.3 we arrived at a model for the length of daylight (in hours) in Philadelphia on the tth day of the year:
L"t# ! 12 % 2.8 sin+ 2( 365
SECTION 3.4 THE CHAIN RULE |||| 205
Use this model to compare how the number of hours of daylight is increasing in Philadelphia on March 21 and May 21.
;81. The motion of a spring that is subject to a frictional force or a damping force (such as a shock absorber in a car) is often modeled by the product of an exponential function and a sine or cosine function. Suppose the equation of motion of a point on such a spring is
s"t# ! 2e#1.5t sin 2(t
where s is measured in centimeters and t in seconds. Find the velocity after t seconds and graph both the position and velocity functions for 0 ' t ' 2.
82.Under certain circumstances a rumor spreads according to the equation
1 p"t# ! 1 % ae#k t
where p" t# is the proportion of the population that knows the rumor at time t and a and k are positive constants. [In Section 9.4 we will see that this is a reasonable equation for p" t#.]
(a)Find limt l, p" t#.
(b)Find the rate of spread of the rumor.
;(c) Graph p for the case a ! 10, k ! 0.5 with t measured in hours. Use the graph to estimate how long it will take for 80% of the population to hear the rumor.
83.A particle moves along a straight line with displacement s" t#, velocity v" t#, and acceleration a" t#. Show that
a"t# ! v"t# ddsv
Explain the difference between the meanings of the derivatives dv(dt and dv(ds.
84. Air is being pumped into a spherical weather balloon. At any time t, the volume of the balloon is V" t# and its radius is r" t#.
(a) What do the derivatives dV(dr and dV(dt represent?
(b) Express dV(dt in terms of dr(dt.
;85. The flash unit on a camera operates by storing charge on a capacitor and releasing it suddenly when the flash is set off. The following data describe the charge Q remaining on the capacitor (measured in microcoulombs, +C) at time t (measured in seconds).
t |
0.00 |
0.02 |
0.04 |
0.06 |
0.08 |
0.10 |
|
|
|
|
|
|
|
Q |
100.00 |
81.87 |
67.03 |
54.88 |
44.93 |
36.76 |
|
|
|
|
|
|
|
(a) Use a graphing calculator or computer to find an exponential model for the charge.
(b) The derivative Q$" t# represents the electric current (measured in microamperes, +A) flowing from the capacitor to the flash bulb. Use part (a) to estimate the current when
t ! 0.04 s. Compare with the result of Example 2 in Section 2.1.

206 |||| CHAPTER 3 DIFFERENTIATION RULES
; 86. The table gives the US population from 1790 to 1860.
Year |
Population |
Year |
Population |
|
|
|
|
1790 |
3,929,000 |
1830 |
12,861,000 |
1800 |
5,308,000 |
1840 |
17,063,000 |
1810 |
7,240,000 |
1850 |
23,192,000 |
1820 |
9,639,000 |
1860 |
31,443,000 |
|
|
|
|
(a)Use a graphing calculator or computer to fit an exponential function to the data. Graph the data points and the exponential model. How good is the fit?
(b)Estimate the rates of population growth in 1800 and 1850 by averaging slopes of secant lines.
(c)Use the exponential model in part (a) to estimate the rates of growth in 1800 and 1850. Compare these estimates with the ones in part (b).
(d)Use the exponential model to predict the population in 1870. Compare with the actual population of 38,558,000. Can you explain the discrepancy?
CAS 87. Computer algebra systems have commands that differentiate functions, but the form of the answer may not be convenient and so further commands may be necessary to simplify the answer.
(a)Use a CAS to find the derivative in Example 5 and compare with the answer in that example. Then use the simplify command and compare again.
(b)Use a CAS to find the derivative in Example 6. What happens if you use the simplify command? What happens if you use the factor command? Which form of the answer would be best for locating horizontal tangents?
CAS 88. (a) Use a CAS to differentiate the function
* x4 # x % 1 f " x# ! x4 % x % 1
and to simplify the result.
(b)Where does the graph of f have horizontal tangents?
(c)Graph f and f $ on the same screen. Are the graphs consistent with your answer to part (b)?
89.Use the Chain Rule to prove the following.
(a)The derivative of an even function is an odd function.
(b)The derivative of an odd function is an even function.
90.Use the Chain Rule and the Product Rule to give an
alternative proof of the Quotient Rule.
[Hint: Write f " x#(t" x# ! f " x#% t" x#& #1.]
91.(a) If n is a positive integer, prove that
dxd "sinnx cos nx# ! n sinn#1x cos"n % 1# x
(b)Find a formula for the derivative of y ! cosnx cos nx that is similar to the one in part (a).
92.Suppose y ! f " x# is a curve that always lies above the x-axis and never has a horizontal tangent, where f is differentiable everywhere. For what value of y is the rate of change of y5 with respect to x eighty times the rate of change of y with respect to x?
93. |
Use the Chain Rule to show that if |
& is measured in degrees, |
|||
|
then |
|
|
|
|
|
|
d |
"sin ! |
( |
cos & |
|
|
d& |
180 |
||
|
|
|
|
||
(This gives one reason for the convention that radian measure is always used when dealing with trigonometric functions in calculus: The differentiation formulas would not be as simple if we used degree measure.)
94. (a) Write ) x ) ! sx2 and use the Chain Rule to show that
dxd ) x ) ! ) xx )
(b)If f " x# ! ) sin x ), find f $" x# and sketch the graphs of f and f $. Where is f not differentiable?
(c)If t" x# ! sin ) x ), find t$" x# and sketch the graphs of t and t$. Where is t not differentiable?
95.If y ! f "u# and u ! t" x#, where f and t are twice differentiable functions, show that
d2 y |
|
d2 y du |
|
2 |
|
dy d2u |
||||
|
! |
|
! |
|
$ |
|
% |
|
|
|
dx2 |
du2 |
dx |
|
du |
dx2 |
|||||
96.If y ! f "u# and u ! t" x#, where f and t possess third derivatives, find a formula for d3y(dx3 similar to the one given in Exercise 95.
|
A P P L I E D |
WHERE SHOULD A PILOT START DESCENT? |
|
|
P R O J E C T |
|
|
|
An approach path for an aircraft landing is shown in the figure on the next page and satisfies the |
||
|
|
||
|
|
||
|
|
following conditions: |
|
|
|
(i) |
The cruising altitude is h when descent starts at a horizontal distance ! from touchdown at |
|
|
|
the origin. |
|
|
(ii) |
The pilot must maintain a constant horizontal speed v throughout descent. |
|
|
|
|
