
- •CONTENTS
- •Preface
- •To the Student
- •Diagnostic Tests
- •1.1 Four Ways to Represent a Function
- •1.2 Mathematical Models: A Catalog of Essential Functions
- •1.3 New Functions from Old Functions
- •1.4 Graphing Calculators and Computers
- •1.6 Inverse Functions and Logarithms
- •Review
- •2.1 The Tangent and Velocity Problems
- •2.2 The Limit of a Function
- •2.3 Calculating Limits Using the Limit Laws
- •2.4 The Precise Definition of a Limit
- •2.5 Continuity
- •2.6 Limits at Infinity; Horizontal Asymptotes
- •2.7 Derivatives and Rates of Change
- •Review
- •3.2 The Product and Quotient Rules
- •3.3 Derivatives of Trigonometric Functions
- •3.4 The Chain Rule
- •3.5 Implicit Differentiation
- •3.6 Derivatives of Logarithmic Functions
- •3.7 Rates of Change in the Natural and Social Sciences
- •3.8 Exponential Growth and Decay
- •3.9 Related Rates
- •3.10 Linear Approximations and Differentials
- •3.11 Hyperbolic Functions
- •Review
- •4.1 Maximum and Minimum Values
- •4.2 The Mean Value Theorem
- •4.3 How Derivatives Affect the Shape of a Graph
- •4.5 Summary of Curve Sketching
- •4.7 Optimization Problems
- •Review
- •5 INTEGRALS
- •5.1 Areas and Distances
- •5.2 The Definite Integral
- •5.3 The Fundamental Theorem of Calculus
- •5.4 Indefinite Integrals and the Net Change Theorem
- •5.5 The Substitution Rule
- •6.1 Areas between Curves
- •6.2 Volumes
- •6.3 Volumes by Cylindrical Shells
- •6.4 Work
- •6.5 Average Value of a Function
- •Review
- •7.1 Integration by Parts
- •7.2 Trigonometric Integrals
- •7.3 Trigonometric Substitution
- •7.4 Integration of Rational Functions by Partial Fractions
- •7.5 Strategy for Integration
- •7.6 Integration Using Tables and Computer Algebra Systems
- •7.7 Approximate Integration
- •7.8 Improper Integrals
- •Review
- •8.1 Arc Length
- •8.2 Area of a Surface of Revolution
- •8.3 Applications to Physics and Engineering
- •8.4 Applications to Economics and Biology
- •8.5 Probability
- •Review
- •9.1 Modeling with Differential Equations
- •9.2 Direction Fields and Euler’s Method
- •9.3 Separable Equations
- •9.4 Models for Population Growth
- •9.5 Linear Equations
- •9.6 Predator-Prey Systems
- •Review
- •10.1 Curves Defined by Parametric Equations
- •10.2 Calculus with Parametric Curves
- •10.3 Polar Coordinates
- •10.4 Areas and Lengths in Polar Coordinates
- •10.5 Conic Sections
- •10.6 Conic Sections in Polar Coordinates
- •Review
- •11.1 Sequences
- •11.2 Series
- •11.3 The Integral Test and Estimates of Sums
- •11.4 The Comparison Tests
- •11.5 Alternating Series
- •11.6 Absolute Convergence and the Ratio and Root Tests
- •11.7 Strategy for Testing Series
- •11.8 Power Series
- •11.9 Representations of Functions as Power Series
- •11.10 Taylor and Maclaurin Series
- •11.11 Applications of Taylor Polynomials
- •Review
- •APPENDIXES
- •A Numbers, Inequalities, and Absolute Values
- •B Coordinate Geometry and Lines
- •E Sigma Notation
- •F Proofs of Theorems
- •G The Logarithm Defined as an Integral
- •INDEX
SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS |||| 99
37.(a) Evaluate the function f !x" ! x2 " !2x&1000" for x ! 1, 0.8, 0.6, 0.4, 0.2, 0.1, and 0.05, and guess the value of
lim |
|
x2 |
" |
2x |
|
|
$ |
1000 % |
|||||
x l0 |
|
|
||||
(b)Evaluate f !x" for x ! 0.04, 0.02, 0.01, 0.005, 0.003, and 0.001. Guess again.
38.(a) Evaluate h!x" ! !tan x " x"&x3 for x ! 1, 0.5, 0.1, 0.05,
0.01, and 0.005. |
tan x " x |
|
|
(b) Guess the value of lim |
. |
||
|
|||
x l0 |
x3 |
||
(c)Evaluate h!x" for successively smaller values of x until you finally reach a value of 0 for h!x". Are you still confident that your guess in part (b) is correct? Explain
why you eventually obtained a value of 0. (In Section 4.4 a method for evaluating the limit will be explained.)
;(d) Graph the function h in the viewing rectangle '"1, 1(
by '0, 1(. Then zoom in toward the point where the graph crosses the y-axis to estimate the limit of h!x" as x approaches 0. Continue to zoom in until you observe distortions in the graph of h. Compare with the results of part (c).
;39. Graph the function f !x" ! sin!%&x" of Example 4 in the viewing rectangle '"1, 1( by '"1, 1(. Then zoom in toward
the origin several times. Comment on the behavior of this function.
40.In the theory of relativity, the mass of a particle with velocity v is
m ! m0
s1 " v2&c2
where m0 is the mass of the particle at rest and c is the speed of light. What happens as v l c"?
;41. Use a graph to estimate the equations of all the vertical asymptotes of the curve
y ! tan!2 sin x" "% ) x ) %
Then find the exact equations of these asymptotes.
; 42. (a) Use numerical and graphical evidence to guess the value of the limit
lim x3 " 1
x l1 sx " 1
(b) How close to 1 does x have to be to ensure that the function in part (a) is within a distance 0.5 of its limit?
2.3CALCULATING LIMITS USING THE LIMIT LAWS
In Section 2.2 we used calculators and graphs to guess the values of limits, but we saw that such methods don’t always lead to the correct answer. In this section we use the following properties of limits, called the Limit Laws, to calculate limits.
LIMIT LAWS Suppose that c is a constant and the limits
|
|
|
|
|
lim f !x" |
and |
lim t!x" |
|
|
|
|
|
|
x la |
|
x la |
|
exist. Then |
|
|
|
|
|
|
||
1. |
lim ' f !x" ! t!x"( ! lim f !x" ! lim t!x" |
|
||||||
|
x la |
|
|
x la |
|
x la |
|
|
2. |
lim ' f !x" " t!x"( ! lim f !x" " lim t!x" |
|
||||||
|
x la |
|
|
x la |
|
x la |
|
|
3. |
lim 'cf !x"( ! c lim f !x" |
|
|
|
||||
|
x la |
|
|
x la |
|
|
|
|
4. |
lim ' f !x"t!x"( ! lim f !x" ! lim t!x" |
|
||||||
|
x la |
|
|
x la |
|
x la |
|
|
|
|
f !x" |
|
lim f !x" |
|
lim t!x" " 0 |
|
|
5. |
lim |
! |
x la |
if |
|
|||
t!x" |
lim t!x" |
|
||||||
|
x la |
|
|
x la |
|
|
||
|
|
|
|
|
|
|
||
x la

100 |||| CHAPTER 2 LIMITS AND DERIVATIVES
SUM LAW
DIFFERENCE LAW
CONSTANT MULTIPLE LAW
PRODUCT LAW
QUOTIENT LAW
y |
|
f |
|
|
|
|
1 |
|
0 |
1 |
x |
g |
|
|
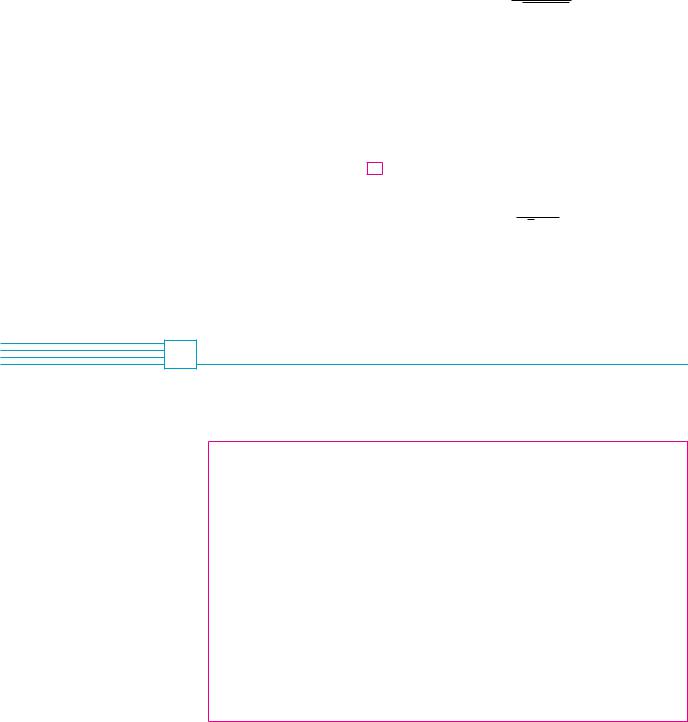
FIGURE 1
These five laws can be stated verbally as follows:
1.The limit of a sum is the sum of the limits.
2.The limit of a difference is the difference of the limits.
3.The limit of a constant times a function is the constant times the limit of the function.
4.The limit of a product is the product of the limits.
5.The limit of a quotient is the quotient of the limits (provided that the limit of the denominator is not 0).
It is easy to believe that these properties are true. For instance, if f !x" is close to L and t!x" is close to M, it is reasonable to conclude that f !x" ! t!x" is close to L ! M. This gives us an intuitive basis for believing that Law 1 is true. In Section 2.4 we give a precise definition of a limit and use it to prove this law. The proofs of the remaining laws are given in Appendix F.
EXAMPLE 1 Use the Limit Laws and the graphs of f and t in Figure 1 to evaluate the following limits, if they exist.
(a) |
lim ' f !x" ! 5t!x"( |
(b) lim ' f !x"t!x"( |
(c) lim |
f !x" |
|
||
t!x" |
|||||||
|
x l"2 |
x l1 |
|
x l2 |
|||
|
|
|
|
||||
SOLUTION |
and t we see that |
|
|
|
|||
(a) |
From the graphs of f |
|
|
|
|||
|
lim f !x" ! 1 |
and |
lim t!x" ! "1 |
||||
|
x l"2 |
|
x l"2 |
|
|
||
Therefore, we have |
|
|
|
|
|
||
|
lim ' f !x" ! 5t!x"( ! lim |
f !x" ! lim '5t!x"( |
(by Law 1) |
||||
|
x l"2 |
x l"2 |
|
x l"2 |
|
|
|
|
|
! lim |
f !x" ! 5 lim t!x" |
(by Law 3) |
|||
|
|
x l"2 |
|
x l"2 |
|
|
|
!1 ! 5!"1" ! "4
(b)We see that limx l1 f !x" ! 2. But limx l1 t!x" does not exist because the left and right limits are different:
lim" t!x" ! "2 |
lim! t!x" ! "1 |
x l1 |
x l1 |
So we can’t use Law 4 for the desired limit. But we can use Law 4 for the one-sided limits:
lim" ' f !x"t!x"( ! 2 ! !"2" ! "4 |
|
lim! ' f !x"t!x"( ! 2 ! !"1" ! "2 |
x l1 |
x l1 |
|
The left and right limits aren’t equal, so limx l1 ' f !x"t!x"( does not exist. |
||
(c) The graphs show that |
|
|
lim f !x" ) 1.4 |
and |
lim t!x" ! 0 |
x l2 |
|
x l2 |
Because the limit of the denominator is 0, we can’t use Law 5. The given limit does not
exist because the denominator approaches 0 while the numerator approaches a nonzero |
|
number. |
M |

SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS |||| 101
If we use the Product Law repeatedly with t!x" ! f !x", we obtain the following law.
POWER LAW |
6. lim ' f !x"(n ! |
lim f !x" n |
where n is a positive integer |
|
|
x la |
[x la |
] |
|
In applying these six limit laws, we need to use two special limits:
7. lim c ! c |
8. lim x ! a |
x la |
x la |
|
|
These limits are obvious from an intuitive point of view (state them in words or draw graphs of y ! c and y ! x), but proofs based on the precise definition are requested in the exercises for Section 2.4.
If we now put f !x" ! x in Law 6 and use Law 8, we get another useful special limit.
9. lim xn ! an |
where n is a positive integer |
x la |
|
|
|
A similar limit holds for roots as follows. (For square roots the proof is outlined in Exercise 37 in Section 2.4.)
10.lim sn x ! sn a where n is a positive integer
x la
(If n is even, we assume that a & 0.)
More generally, we have the following law, which is proved as a consequence of Law 10 in Section 2.5.
ROOT LAW |
11. lim n |
f !x) |
! n |
lim f !x) |
where n is a positive integer |
|
x la s |
|
sx la |
|
|
[If n is even, we assume that lim f !x" & 0.]
x la
EXAMPLE 2 Evaluate the following limits and justify each step.
(a) lim !2x2 " 3x ! 4" |
|
(b) lim |
|
x3 |
! 2x2 " 1 |
|
|
|
|
|
5 " 3x |
|
|||
x l5 |
|
|
x l"2 |
|
|
||
SOLUTION |
|
|
|
|
|
|
|
(a) |
lim !2x2 " 3x ! 4" ! lim !2x2 " " lim !3x" ! lim 4 |
(by Laws 2 and 1) |
|||||
|
x l5 |
x l5 |
x l5 |
|
x l5 |
|
|
|
|
! 2 lim x2 " 3 lim x ! lim 4 |
(by 3) |
||||
|
|
x l5 |
x l5 |
x l5 |
|
||
|
|
! 2!52 " " 3!5" ! 4 |
|
(by 9, 8, and 7) |
|||
|
|
! 39 |
|
|
|
|
|

102 |||| CHAPTER 2 LIMITS AND DERIVATIVES
NEWTON AND LIMITS
Isaac Newton was born on Christmas Day in 1642, the year of Galileo’s death. When he entered Cambridge University in 1661 Newton didn’t know much mathematics, but he learned quickly by reading Euclid and Descartes and by attending the lectures of Isaac Barrow.
Cambridge was closed because of the plague in 1665 and 1666, and Newton returned home to reflect on what he had learned. Those two years were amazingly productive for at that time he made four of his major discoveries: (1) his representation of functions as sums of infinite series, including the binomial theorem; (2) his work on differential and integral calculus; (3) his laws of motion and law of universal gravitation; and (4) his prism experiments on the nature of light and color. Because of a fear of controversy and criticism, he was reluctant to publish his discoveries and it wasn’t until 1687, at the urging of the astronomer Halley, that Newton published Principia Mathematica. In this work, the greatest scientific treatise ever written, Newton set forth his version of calculus and used it to investigate mechanics, fluid dynamics, and wave motion, and to explain the motion of planets and comets.
The beginnings of calculus are found in the calculations of areas and volumes by ancient Greek scholars such as Eudoxus and Archimedes. Although aspects of the idea of a limit are implicit in their “method of exhaustion,” Eudoxus and Archimedes never explicitly formulated the concept of a limit. Likewise, mathematicians such as Cavalieri, Fermat, and Barrow, the immediate precursors of Newton in the development of calculus, did not actually use limits. It was Isaac Newton who was the first to talk explicitly about limits. He explained that the main idea behind limits is that quantities “approach nearer than by any given difference.” Newton stated that the limit was the basic concept in calculus, but it was left to later mathematicians like Cauchy to clarify his ideas about limits.
(b) We start by using Law 5, but its use is fully justified only at the final stage when we see that the limits of the numerator and denominator exist and the limit of the denominator is not 0.
|
x |
3 |
! 2x |
2 |
" 1 |
|
|
lim !x3 ! 2x2 " 1" |
|
|
|||||
lim |
|
|
! |
x l"2 |
|
|
|
|
(by Law 5) |
||||||
|
|
5 " 3x |
|
" 3x" |
|
||||||||||
x l"2 |
|
|
|
|
lim !5 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
x l"2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim x3 ! 2 lim x2 " lim 1 |
|
||||||
|
|
|
|
|
|
! |
x l"2 |
x l"2 |
x l"2 |
(by 1, 2, and 3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
lim 5 " 3 lim x |
|
||||
|
|
|
|
|
|
|
|
|
|
x l"2 |
x l"2 |
|
|
||
|
|
|
|
|
|
! |
|
!"2"3 ! 2!"2"2 " 1 |
|
|
(by 9, 8, and 7) |
||||
|
|
|
|
|
|
5 " 3!"2" |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
! |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
" |
|
|
|
|
|
|
M |
||
|
|
|
|
|
|
11 |
|
|
|
|
|
||||

 If we let f !x" ! 2x2 " 3x ! 4, then f !5" ! 39. In other words, we would have gotten the correct answer in Example 2(a) by substituting 5 for x. Similarly, direct substitution provides the correct answer in part (b). The functions in Example 2 are a polynomial and a rational function, respectively, and similar use of the Limit Laws proves that direct substitution always works for such functions (see Exercises 53 and 54). We state this fact as follows.
If we let f !x" ! 2x2 " 3x ! 4, then f !5" ! 39. In other words, we would have gotten the correct answer in Example 2(a) by substituting 5 for x. Similarly, direct substitution provides the correct answer in part (b). The functions in Example 2 are a polynomial and a rational function, respectively, and similar use of the Limit Laws proves that direct substitution always works for such functions (see Exercises 53 and 54). We state this fact as follows.
DIRECT SUBSTITUTION PROPERTY If f is a polynomial or a rational function and a is in the domain of f, then
lim f !x" ! f !a"
x la
Functions with the Direct Substitution Property are called continuous at a and will be studied in Section 2.5. However, not all limits can be evaluated by direct substitution, as the following examples show.
EXAMPLE 3 Find lim |
x2 |
" 1 |
. |
|
x |
" 1 |
|||
x l1 |
|
SOLUTION Let f !x" ! !x2 " 1"#!x " 1". We can’t find the limit by substituting x ! 1 because f !1" isn’t defined. Nor can we apply the Quotient Law, because the limit of the denominator is 0. Instead, we need to do some preliminary algebra. We factor the numerator as a difference of squares:
x2 " 1 |
! |
!x " 1"!x ! 1" |
x " 1 |
x " 1 |
The numerator and denominator have a common factor of x " 1. When we take the limit as x approaches 1, we have x " 1 and so x " 1 " 0. Therefore we can cancel the common factor and compute the limit as follows:
lim |
x2 |
" 1 |
! lim |
!x " 1"!x ! 1" |
! lim !x ! 1" ! 1 ! 1 ! 2 |
|
x |
" 1 |
x " 1 |
||||
x l1 |
x l1 |
x l1 |
The limit in this example arose in Section 2.1 when we were trying to find the tangent to the parabola y ! x2 at the point !1, 1". M
N OT E In Example 3 we were able to compute the limit by replacing the given function f !x" ! !x2 " 1"#!x " 1" by a simpler function, t!x" ! x ! 1, with the same limit. This is

y
3y=Ä
2
1
0 |
1 |
2 |
3 |
x |
y |
|
|
|
|
3 |
|
|
y=© |
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
0 |
1 |
2 |
3 |
x |
FIGURE 2
The graphs of the functions f (from Example 3) and g (from Example 4)
SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS |||| 103
valid because f !x" ! t!x" except when x ! 1, and in computing a limit as x approaches 1 we don’t consider what happens when x is actually equal to 1. In general, we have the following useful fact.
If f !x" ! t!x" when x " a, then lim |
f !x" ! lim t!x", provided the limits exist. |
|
|
x la |
|
x la |
|
|
|
|
|
EXAMPLE 4 Find lim t!x" where |
|
|
|
x l1 |
|
|
|
x ! 1 |
if x " 1 |
|
|
t!x" ! $# |
if x ! 1 |
|
|
SOLUTION Here t is defined at x ! 1 and t!1" ! |
#, but the value of a limit as x approaches |
||
1 does not depend on the value of the function at 1. Since t!x" ! x ! 1 for x " 1, we |
|
||
have |
|
|
|
lim t!x" ! lim !x ! 1" ! 2 |
M |
||
x l1 |
x l1 |
|
|
Note that the values of the functions in Examples 3 and 4 are identical except when x ! 1 (see Figure 2) and so they have the same limit as x approaches 1.
|
EXAMPLE 5 Evaluate lim |
|
!3 ! h"2 " 9 |
. |
|
|
|
|
|
|
|
|
|||||||||
V |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
SOLUTION If we define |
|
h l0 |
|
|
h |
|
!3 ! h"2 |
" 9 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
F!h" |
! |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
then, as in Example 3, we can’t compute limh l0 F!h" by letting h ! 0 since F!0" is |
|
||||||||||||||||||||
undefined. But if we simplify F!h" algebraically, we find that |
|
|
|||||||||||||||||||
|
F!h" ! |
!9 ! 6h ! h2 " " 9 |
! |
|
6h ! h2 |
|
! 6 ! h |
|
|||||||||||||
|
|
|
|
|
|
h |
|
|
|
|
|
|
h |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(Recall that we consider only h " 0 when letting h approach 0.) Thus |
|
||||||||||||||||||||
|
|
|
lim |
|
!3 ! h"2 |
" 9 |
|
! lim |
!6 ! h" ! 6 |
M |
|||||||||||
|
|
|
|
|
|
h |
|
|
|
|
|||||||||||
|
|
|
h l0 |
|
|
|
|
|
|
|
h l0 |
|
|
|
|
|
|
||||
|
|
s |
|
|
|
" 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
EXAMPLE 6 Find lim |
t2 ! 9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t l0 |
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
SOLUTION We can’t apply the Quotient Law immediately, since the limit of the denominator is 0. Here the preliminary algebra consists of rationalizing the numerator:
lim
t l0
s |
t2 ! 9 |
" 3 |
! lim |
|
|
s |
t2 ! 9 |
" 3 |
! |
s |
t2 |
! 9 |
|
! 3 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
t |
2 |
|
t l0 |
|
|
|
|
|
t |
2 |
|
|
|
|
|
st |
2 |
! 9 |
! 3 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
! lim |
|
|
|
|
!t2 ! 9" " 9 |
|
|
! lim |
|
|
|
|
t2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
t l0 |
|
|
t2( t2 |
! 9 ! 3) |
|
|
|
|
t l0 t2( t2 |
! 9 ! 3) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|||
|
|
|
|
! lim |
1 |
|
|
|
|
! |
|
|
|
|
|
|
1 |
|
|
|
! |
1 |
! |
1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
t l0 |
st2 ! 9 ! 3 |
|
|
|
slimt l0 !t2 ! 9" |
! 3 |
|
3 ! 3 |
|
6 |
||||||||||||||||||
This calculation confirms the guess that we made in Example 2 in Section 2.2. |
M |

104 |||| CHAPTER 2 LIMITS AND DERIVATIVES
N The result of Example 7 looks plausible from Figure 3.
y |
|
|
y=|x| |
0 |
x |
Some limits are best calculated by first finding the leftand right-hand limits. The following theorem is a reminder of what we discovered in Section 2.2. It says that a two-sided limit exists if and only if both of the one-sided limits exist and are equal.
1 THEOREM lim f !x" ! L |
if and only if |
lim f !x" ! L ! lim f !x" |
|
x la |
|
x la" |
x la! |
|
|
|
|
When computing one-sided limits, we use the fact that the Limit Laws also hold for one-sided limits.
x l0 |
% |
x |
% |
! |
0. |
|
|
|
|
EXAMPLE 7 Show that lim |
|
|
|
|
|
|
|||
SOLUTION Recall that |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
if x & 0 |
|
|
|
|
% x % ! $"x if x % 0 |
|||||
Since % x % ! x for x $ 0, we have |
|
|
% |
|
|
||||
|
|
|
|
|
lim |
x |
! lim x ! 0 |
||
|
|
|
|
x l0! % |
|
|
x l0! |
||
FIGURE 3 |
For x % 0 we have % x % ! "x and so |
|
|
|
lim |
|
x |
% |
! lim !"x" ! 0 |
|
|||||
|
|
xl0" % |
|
|
xl0" |
|
||||||
Therefore, by Theorem 1, |
|
|
|
|
|
|
% |
|
% |
|
|
|
|
|
|
|
|
|
x l0 |
x |
! 0 |
|
|||
|
|
|
|
|
|
lim |
|
|
M |
|||
|
EXAMPLE 8 Prove that lim |
% x % |
|
does not exist. |
|
|||||||
V |
|
|
||||||||||
x |
|
|||||||||||
|
x l0 |
|
|
|
|
|
|
|
|
|
||
y= |x|x |
y |
SOLUTION |
lim |
% x % |
! lim |
x |
! lim 1 ! 1 |
|
1 |
|
x l0! |
x |
x l0! |
x |
x l0! |
|
|
|
0 |
x |
lim |
% x % |
! lim |
"x ! lim !"1" ! "1 |
|
|
|
x l0" |
x |
x l0" |
x |
x l0" |
|
||
|
|
_1 |
|
|
|
|
|
|
|
|
Since the rightand left-hand limits are different, it follows from Theorem 1 that |
|
|||||
|
|
limx l0 |
% x %#x does not exist. The graph of the function f !x" ! % x %#x is shown in |
|
||||
FIGURE 4 |
|
Figure 4 and supports the one-sided limits that we found. |
M |
|||||
EXAMPLE 9 If |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
if |
x $ 4 |
||||
|
|
|
|
x " 4 |
|||||||
|
|
|
f !x" ! $8s" 2x |
if x % 4 |
|||||||
determine whether limx l4 f !x" exists. |
|
|
|
|
|
|
|
||||
|
Since f !x" ! s |
|
for x $ 4, we have |
|
|
|
|
||||
SOLUTION |
x " 4 |
|
|
|
|
||||||
N It is shown in Example 3 in |
|
lim f !x" ! lim |
|
|
|
|
|
|
! 0 |
||
Section 2.4 that lim x l0! sx ! 0. |
|
x " 4 |
! |
s |
4 " 4 |
||||||
|
x l4! |
x l4! s |
|
|
|
|
|
|
|||

y
0 |
4 |
x |
FIGURE 5
N Other notations for &x ' are (x) and x . The greatest integer function is sometimes called the
floor function.
y
4
3
2 |
y=[ x] |
1
0 |
1 |
2 |
3 |
4 |
5 |
x |
SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS |||| 105
Since f !x" ! 8 " 2x for x % 4, we have
lim f !x" ! lim !8 " 2x" ! 8 " 2 ! 4 ! 0
x l4" x l4"
The rightand left-hand limits are equal. Thus the limit exists and
lim f !x" ! 0
x l4
The graph of f is shown in Figure 5. |
|
|
M |
EXAMPLE 10 The greatest integer function is defined by &x' ! the largest integer |
|||
that is less than or equal to x. (For instance, &4' ! 4, &4.8' ! 4, &#' ! 3, |
&s |
|
' ! 1, |
2 |
|||
&"21 ' ! "1.) Show that limx l3 &x' does not exist. |
|
|
|
SOLUTION The graph of the greatest integer function is shown in Figure 6. Since &x' ! 3 for 3 ' x % 4, we have
lim &x' ! lim 3 ! 3
x l3! x l3!
Since &x' ! 2 for 2 ' x % 3, we have
lim &x' ! lim 2 ! 2
x l3" x l3"
FIGURE 6 |
|
|
Because these one-sided limits are not equal, limx l3 &x' does not exist by Theorem 1. M |
||||
|
|
|
|
|
|||
Greatest integer function |
|
The next two theorems give two additional properties of limits. Their proofs can be |
|||||
|
|
|
|
|
|||
|
|
|
|
|
found in Appendix F. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
THEOREM If f !x" ' t!x" when x is near a (except possibly at a) and the limits |
|
|
|
|
|
|
of f and t both exist as x approaches a, then |
||
|
|
|
|
|
|
lim f !x" ' lim t!x" |
|
|
|
|
|
|
|
x la |
x la |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
THE SQUEEZE THEOREM If f !x" ' t!x" ' h!x" when x is near a (except |
|
|
|
|
|
|
possibly at a) and |
|
|
|
y |
|
|
|
|
lim f !x" ! lim h!x" ! L |
|
|
|
|
h |
|
x la |
x la |
|
|
|
|
|
|
|
|
|
|
L |
|
|
g |
then |
lim t!x" ! L |
|
|
|
|
|
|
|
x la |
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
||
|
|
|
|
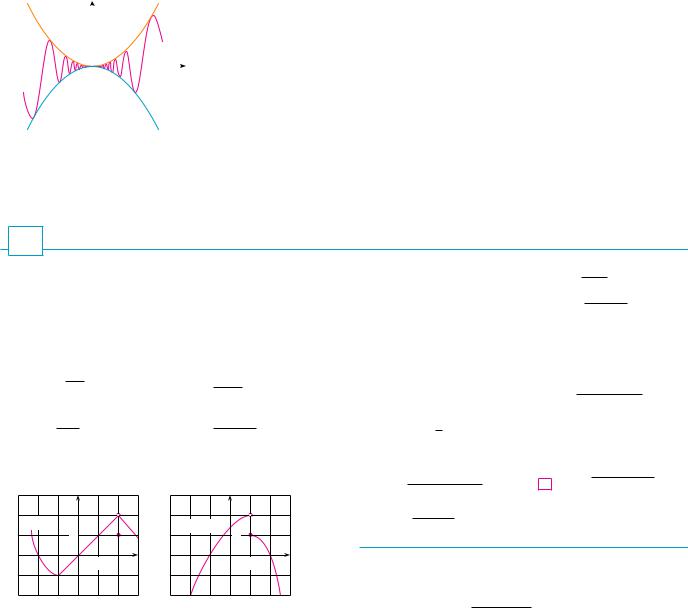
The Squeeze Theorem, which is sometimes called the Sandwich Theorem or the Pinch- |
|||
|
|
|
|
|
ing Theorem, is illustrated by Figure 7. It says that if t!x" is squeezed between f !x" and |
||
0 |
|
a |
x |
||||
|
|
|
|
|
h!x" near a, and if f and h have the same limit L at a, then t is forced to have the same |
||
|
|
|
|
|
|||
FIGURE 7 |
|
|
limit L at a. |
|
|||
106 |||| CHAPTER 2 LIMITS AND DERIVATIVES
|
|
|
|
|
|
EXAMPLE 11 Show that lim x2 sin |
|
1 |
|
! 0. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x l0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
SOLUTION |
First note that we cannot use |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
| |
|
|
lim x2 sin |
|
1 |
! lim x2 ! lim sin |
1 |
|
|||||||||
|
|
|
|
x |
x |
|||||||||||||||
|
|
|
|
|
|
|
x l0 |
|
x l0 |
|
|
x l0 |
||||||||
|
|
|
|
|
because limx l0 sin!1#x" does not exist (see Example 4 in Section 2.2). However, since |
|||||||||||||||
|
|
|
|
|
|
|
"1 ' sin |
1 |
|
' 1 |
|
|
||||||||
|
|
|
|
|
|
|
x |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
y=≈ |
|
|
we have, as illustrated by Figure 8, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
"x2 ' x2 sin |
|
' x2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
|
|
|
|
|
|
We know that |
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
x |
lim x2 ! 0 |
|
|
|
and |
|
lim !"x2 " ! 0 |
||||||||||
|
|
|
|
|
|
|
x l0 |
|
|
|
|
|
|
|
|
x l0 |
|
|
||
|
|
y=_≈ |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Taking |
f !x" ! "x2, !x" ! x2 sin!1#x", and h!x" ! x2 in the Squeeze Theorem, we |
|||||||||||||||
FIGURE 8 |
|
|
|
|
obtain |
lim x2 sin |
1 |
! 0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
y=≈"sin(1/x) |
|
|
|
|
|
|
|
M |
||||||||||||
|
|
|
|
|
|
|
x |
|||||||||||||
|
|
|
|
|
|
|
x l0 |
|
|
|
|
|
|
|
||||||
2.3EXERCISES
1. |
Given that |
|
|
|
|
|
|
(c) |
lim ( f !x"t!x") |
(d) |
lim |
f !x" |
|||||||||
|
lim f !x" ! 4 |
lim t!x" ! "2 |
|
lim h!x" ! 0 |
|
|
x l0 |
|
|
|
|
|
|
x l"1 |
t!x" |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x l2 |
|
|
x l2 |
|
|
x l2 |
|
|
(e) |
lim (x3f !x") |
|
|
(f) |
lim |
3 ! f !x" |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
find the limits that exist. If the limit does not exist, explain why. |
|
x l2 |
|
|
|
|
|
|
x l1 s |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
(a) lim ( f !x" ! 5t!x") |
(b) lim ( t!x")3 |
|
3–9 Evaluate the limit and justify each step by indicating the |
|||||||||||||||||
|
x l2 |
|
|
|
x l2 |
|
|
|
appropriate Limit Law(s). |
|
|
|
|
||||||||
|
|
|
|
|
(d) lim 3f !x" |
|
|
|
|
|
|||||||||||
|
(c) lim |
s |
f !x" |
|
|
3. |
lim !3x |
4 |
! 2x |
2 |
" x ! 1" |
4. |
lim |
2x2 ! 1 |
|||||||
|
x l2 |
|
|
x l2 |
t!x" |
|
|
|
2 ! 6x " 4 |
||||||||||||
|
|
|
|
|
|
|
|
x l"2 |
|
|
|
|
|
|
|
x l2 x |
|||||
|
(e) lim |
t!x" |
|
(f) lim |
t!x"h!x" |
5. |
lim (1 ! |
|
x )!2 " 6x2 ! x3" |
6. lim !t2 ! 1"3!t ! 3"5 |
|||||||||||
|
x l2 |
h!x" |
|
x l2 |
|
f !x" |
|
3 |
|||||||||||||
2. |
The graphs of f and t are given. Use them to evaluate each |
x l8 |
|
|
|
s |
|
|
|
|
t l"1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
limit, if it exists. If the limit does not exist, explain why. |
lim |
|
|
|
1 |
! 3x |
3 |
8. |
lim |
|
u4 ! 3u ! 6 |
|||||||||
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|||||||
|
|
|
y |
|
|
y |
|
*1 ! 4x2 ! 3x4 + |
|
||||||||||||
|
|
|
|
|
|
|
x l1 |
|
u l"2 s |
|
|||||||||||
|
y=Ä |
1 |
|
y=© |
1 |
|
9. |
lim |
|
16 " x2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
x l4" s |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
x |
|
0 |
1 |
x |
(a) What is wrong with the following equation? |
||||||||||||
|
|
|
|
|
|
|
|
|
10. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 ! x " 6 |
! x ! 3 |
|
|
|
|
(a) lim ( f !x" ! t!x") |
|
(b) lim ( f !x" ! t!x") |
|
|
|
|
|
|
|
|
x " 2 |
|
|
|||||||
|
x l2 |
|
|
|
x l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

SECTION 2.3 CALCULATING LIMITS USING THE LIMIT LAWS |||| 107
(b) In view of part (a), explain why the equation
lim |
x2 |
! x " 6 |
! lim !x ! 3" |
|
x " 2 |
||
x l2 |
|
x l2 |
is correct.
11–30 Evaluate the limit, if it exists.
11. |
lim |
|
x2 ! x " 6 |
|
|
|
|
12. |
lim |
|
|
|
x2 ! 5x ! 4 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
x " 2 |
|
|
|
|
|
|
|
|
|
|
x2 ! 3x " 4 |
|||||||||||||||||||||||||||
|
x l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x l"4 |
|
||||||||||||||||||||||||||||
13. |
lim |
|
x2 " x ! 6 |
|
|
|
|
14. |
lim |
|
|
|
|
|
x2 " 4x |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
x " 2 |
|
|
|
|
|
|
|
|
|
x2 " 3x " 4 |
||||||||||||||||||||||||||||
|
x l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x l4 |
|
|
|||||||||||||||||||||||||||
15. |
lim |
|
|
|
|
|
|
t2 " 9 |
|
|
|
|
|
|
|
16. |
lim |
|
|
|
|
|
|
|
x2 " 4x |
|
||||||||||||||||||
|
|
2t2 ! 7t ! 3 |
|
|
|
|
|
|
x2 " 3x " 4 |
|||||||||||||||||||||||||||||||||||
|
t l"3 |
|
|
|
|
|
|
x l"1 |
|
|||||||||||||||||||||||||||||||||||
17. |
lim |
!4 ! h"2 " 16 |
|
|
|
18. |
lim |
|
x3 " 1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
x2 " 1 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
h l0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x l1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
19. |
lim |
|
|
|
x ! 2 |
|
|
|
|
|
|
|
20. |
lim |
|
!2 ! h"3 " 8 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|||||||
|
x l"2 x3 ! 8 |
|
|
|
|
|
|
|
|
h l0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
9 " t |
|
|
|
|
|
|
|
|
lim |
s |
|
|
" 1 |
|
|
|||||||||||||||||||||||||
21. |
lim |
|
|
|
|
|
|
|
|
|
|
22. |
1 ! h |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
t l9 |
3 " st |
|
|
|
|
|
|
|
|
h l0 |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
s |
|
|
|
|
" 3 |
|
|
|
|
|
|
|
|
|
|
x2 ! 2x ! 1 |
|
||||||||||||||||||||||||
23. |
lim |
|
x ! 2 |
|
|
|
24. |
lim |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x4 " 1 |
|||||||||||||||||||||||||
|
x l7 |
|
|
|
|
|
|
x " 7 |
|
|
|
|
|
|
|
|
x l"1 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
25. |
lim |
|
4 |
|
x |
|
|
|
|
|
|
|
26. |
lim |
|
|
|
1 |
|
" |
|
|
1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* t |
|
|
t |
2 ! t + |
||||||||||||||||
|
x l"4 4 ! x |
|
|
|
|
|
|
|
|
t l0 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 " s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!3 ! h""1 " 3"1 |
|
|||||||||||||||||||
27. |
lim |
|
|
|
x |
|
|
|
|
|
|
|
28. |
lim |
|
|
||||||||||||||||||||||||||||
|
16x " x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
||||||||||||||||||||||||||
|
x l16 |
|
|
|
|
|
|
|
+ |
|
h l0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
s |
|
|
|
|
|
" 5 |
|
|
|||||||||
29. |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
30. |
lim |
|
|
x2 ! 9 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
x ! 4 |
|||||||||||||||||
|
t l0 *ts1 ! t |
|
|
|
|
|
|
x l"4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||
;31. (a) Estimate the value of
lim
x
x l0 s1 ! 3x " 1
by graphing the function f !x" ! x#(s1 ! 3x " 1).
(b)Make a table of values of f !x" for x close to 0 and guess the value of the limit.
(c)Use the Limit Laws to prove that your guess is correct.
;32. (a) Use a graph of
f !x" ! s3 ! x " s3 x
to estimate the value of limx l0 f !x" to two decimal places.
(b)Use a table of values of f !x" to estimate the limit to four decimal places.
(c)Use the Limit Laws to find the exact value of the limit.
;33. Use the Squeeze Theorem to show that
limx l0 !x2 cos 20#x" ! 0. Illustrate by graphing the
functions f !x" ! "x2, t!x" ! x2 cos 20#x, and h!x" ! x2 on the same screen.
;34. Use the Squeeze Theorem to show that
|
|
|
|
|
# |
|
|
lim |
s |
x3 |
! x2 |
sin |
! 0 |
||
|
|||||||
x |
|||||||
x l0 |
|
|
|
|
Illustrate by graphing the functions f, t, and h (in the notation of the Squeeze Theorem) on the same screen.
35.If 4x " 9 ' f !x" ' x2 " 4x ! 7 for x & 0, find limx l4 f !x".
36.If 2x ' t!x" ' x4 " x2 ! 2 for all x, evaluate limx l1 t!x".
37. |
Prove that lim x4 cos |
2 |
! 0. |
|||
x |
||||||
|
x l0 |
|
|
|
||
|
|
|
|
|
# |
|
38. |
Prove that lim |
x esin! |
||||
#x" ! 0. |
||||||
|
x l0! s |
|
|
|
|
|
39– 44 Find the limit, if it exists. If the limit does not exist, explain why.
39.lim (2x ! % x " 3 %)
x l3
2x " 1
41.lim % 2x3 " x2 %
xl0.5"
43.lim *1 " % 1 % +
xl0" x x
40. lim |
2x ! 12 |
|
% x ! 6 % |
||
x l"6 |
42.lim 2 " % x %
xl"2 2 ! x
44. lim |
|
1 |
" |
1 |
|
|
*x |
% x % + |
|||||
x l0! |
|
|||||
45. The signum (or sign) function, denoted by sgn, is defined by
|
"1 |
if x % 0 |
sgn x ! |
"0 |
if x ! 0 |
|
$"1 |
if x $ 0 |
(a)Sketch the graph of this function.
(b)Find each of the following limits or explain why it does not exist.
(i) |
lim sgn x |
(ii) |
lim |
|
sgn x |
|
|
x l0! |
|
x l0" |
|
|
|
(iii) |
lim sgn x |
(iv) |
lim |
% |
sgn x |
% |
|
x l0 |
|
x l0 |
|
||
46. Let |
|
|
|
|
|
|
|
|
4 " x2 |
if |
x ' 2 |
|
|
|
f !x" |
! $x " 1 |
if x $ 2 |
|
||
(a)Find limx l2" f !x" and limx l2! f !x".
(b)Does lim x l2 f !x" exist?
(c)Sketch the graph of f.
x2 " 1
47.Let F!x" ! % x " 1 % .
(a)Find
(i) lim F!x" |
(ii) lim |
F!x" |
x l1! |
x l1" |
|

108|||| CHAPTER 2 LIMITS AND DERIVATIVES
(b)Does limx l1 F!x" exist?
(c)Sketch the graph of F.
48.Let
|
|
x |
if |
x % 1 |
|
|
|
t!x" ! |
3 |
if |
x ! 1 |
|
|
|
2 " x2 |
if 1 % x ' 2 |
|
|
||
|
|
x " 3 |
if |
x $ 2 |
|
|
(a) Evaluate each of the following limits, if it exists. |
||||||
(i) |
lim" t!x" |
(ii) |
lim t!x" |
(iii) |
t!1" |
|
|
x l1 |
|
x l1 |
|
|
|
(iv) |
lim" t!x" |
(v) |
lim! t!x" |
(vi) |
lim t!x" |
|
|
x l2 |
|
x l2 |
|
x l2 |
|
(b)Sketch the graph of t.
49.(a) If the symbol & ' denotes the greatest integer function defined in Example 10, evaluate
(i) |
lim |
&x' |
(ii) |
lim |
&x' |
(iii) lim &x' |
|
x l"2! |
|
x l"2 |
|
x l"2.4 |
|
(b) If n is an integer, evaluate |
|
|
||||
(i) |
lim |
&x' |
(ii) |
lim |
&x' |
|
|
x ln" |
|
|
x ln! |
|
|
(c) For what values of a does limx la &x' exist?
50. Let f !x" ! &cos x', "# ' x ' #.
(a)Sketch the graph of f.
(b)Evaluate each limit, if it exists.
(i) |
lim |
f !x" |
(ii) |
lim |
f !x" |
|
|
x l0 |
|
|
|
# |
" |
|
|
|
|
x l! #2" |
||
(iii) |
lim |
f !x" |
(iv) |
lim |
f !x" |
|
|
x l! |
#2" |
! |
|
x l #2 |
|
|
# |
|
# |
|
||
(c) For what values of a does limx la f !x" exist?
51.If f !x" ! & x' ! &"x', show that limx l2 f !x" exists but is not equal to f !2".
52.In the theory of relativity, the Lorentz contraction formula
L ! L0 s1 " v 2#c2
expresses the length L of an object as a function of its velocity v with respect to an observer, where L0 is the length of the object at rest and c is the speed of light. Find limv lc" L and interpret the result. Why is a left-hand limit necessary?
53. If p is a polynomial, show that limxla p!x" ! p!a".
54. If r is a rational function, use Exercise 53 to show that limx la r!x" ! r!a" for every number a in the domain of r.
55. If lim |
f !x" " 8 |
! 10, find lim f !x". |
|
x " 1 |
|||
x l1 |
x l1 |
56.If lim f !x2" ! 5, find the following limits.
xl0 x
(a) lim f !x" |
|
(b) lim |
f !x" |
|
x |
||
x l0 |
|
x l0 |
|
57. If |
|
|
|
x2 |
if |
x is rational |
|
f !x" ! $0 |
if |
x is irrational |
|
prove that limx l0 f !x" ! 0.
58.Show by means of an example that limx la ( f !x" ! t!x") may exist even though neither limx la f !x" nor limx la t!x" exists.
59.Show by means of an example that limx la ( f !x"t!x") may exist even though neither limx la f !x" nor limx la t!x" exists.
60.Evaluate lim s6 " x " 2 .
xl2 s3 " x " 1
61.Is there a number a such that
lim |
3x2 |
! ax ! a ! 3 |
|
x2 ! x " 2 |
|
x l"2 |
|
exists? If so, find the value of a and the value of the limit.
62.The figure shows a fixed circle C1 with equation
!x " 1"2 ! y2 ! 1 and a shrinking circle C2 with radius r and center the origin. P is the point !0, r", Q is the upper point of intersection of the two circles, and R is the point of intersection of the line PQ and the x-axis. What happens to R as C2 shrinks, that is, as r l 0!?
PQ
Cª
0 |
R |
x |
CÁ
