3.4.2. Переход от канонической формы модели задачи линейного программирования к стандартной

Пусть ЗЛП задана в канонической форме:

,

,

.

Первый способ

Каждое ограничение-равенство может быть заменено эквивалентной системой неравенств:

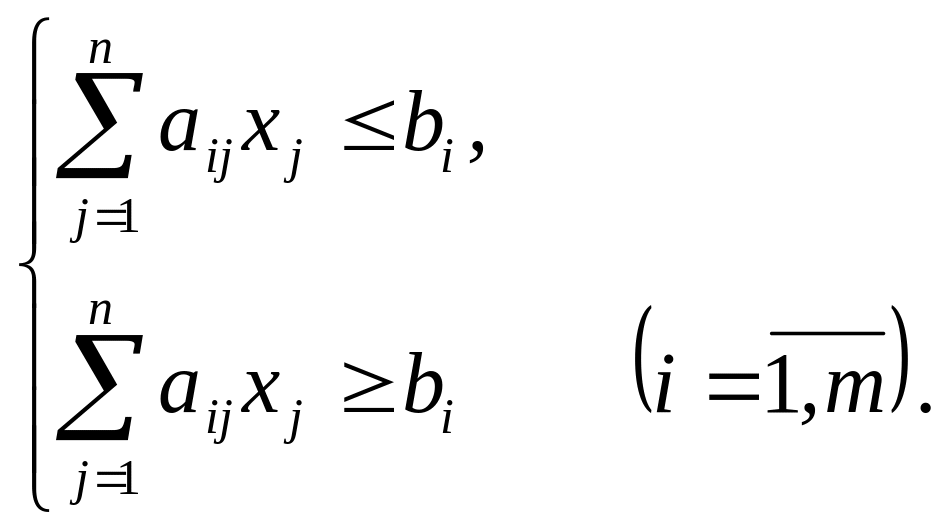
Неравенства умножением обеих частей на –1 превращаются в неравенства .

Второй способ

Предположим, в системе ограничений:

канонической формы модели и все m уравнений линейно независимы (ранг системы ). В этом случае система имеет бесчисленное множество решений. Ее можно разрешить относительно m переменных , например методом Жордана–Гаусса, если векторы-столбцы коэффициентов при этих неизвестных линейно независимы:

. (3.7)

В этом случае являются базисными переменными, а свободные переменные.

Целевую функцию также выразим через свободные переменные, подставив значения из равенств (3.7) в функцию цели.

В результате преобразования получим:

,

так как , то из равенств (3.7) имеем:

.

Стандартная форма модели ЗЛП примет вид:

,

,

.

3. 5. Выпуклые множества

Определение 3.4. Вектор называется выпуклой линейной комбинацией векторов если коэффициенты удовлетворяют условиям:

.

В частности, выпуклой линейной комбинацией двух векторов (точек) X ¹ и X ² является вектор:

, где

Определение 3.5. Множество D векторов (точек) линейного пространства называется выпуклым, если вместе с любыми его двумя точками и ему принадлежит отрезок, соединяющий эти точки.

Аналитически условие выпуклости множества записывается следующим образом: для любых , и любого выполняется условие:

.

На рис. 3.2 изображены выпуклые множества (а, б) и множество, не являющееся выпуклым (в).

Рис. 3.2. Примеры множеств

Определение 3.6. Точка X¹ выпуклого множества D называется его угловой (крайней) точкой, если она не может быть представлена выпуклой линейной комбинацией двух других точек этого множества (не является внутренней точкой ни для какого отрезка, концы которого принадлежат множеству D).

Например, крайними точками треугольника являются его вершины, крайними точками круга – точки окружности, которая его ограничивает.

Однако не всякое выпуклое множество имеет крайние точки. Прямая, плоскость, полуплоскость, пространство, полупространство угловых точек не имеют.

Определение 3.7. Выпуклым многогранником (многоугольником на плоскости) называется замкнутое ограниченное выпуклое множество, имеющее конечное число крайних (угловых) точек.

Теорема 3.2. Любая точка выпуклого многогранника может быть представлена как выпуклая линейная комбинация его вершин (крайних точек).

4. Графический метод решения задачи линейного программирования

Рассмотрим графический метод решения ЗЛП в стандартной форме с двумя переменными, т.е. задачи вида:

Найти вектор удовлетворяющий системе ограничений:

для которого функция цели Z = c₁x₁+c₂x₂ достигает максимума.

Графический метод решения ЗЛП условно можно разбить на два этапа:

1. Построение ОДР ЗЛП.

2. Нахождение среди всех точек ОДР такой точки в которой целевая функция принимает максимальное значение.

Перейдем к рассмотрению этих этапов.

Этап 1