6.2. Алгебра симплекс-метода

Дадим изложение симплекс-метода для ЗЛП вида:

,

при ограничениях

Пусть ранг матрицы системы ограничений равен m, и все , . В матричной форме ЗЛП имеет вид:

,

.

Запишем условие задачи в виде таблицы:

Предположим, что являются базисными переменными (при необходимости можно произвести перенумерацию). Тогда первые m столбцов матрицы:

образуют квадратную невырожденную матрицу B (базисную матрицу) m-го порядка, а оставшиеся (n – m) столбцов дают матрицу F размеров . Аналогичным образом вектор с разбивается на два вектора , где вектор коэффициентов при базисных неизвестных ; вектор при остальных свободных неизвестных. – функции цели Z. Вектор .

Тогда исходная таблица примет вид:

		0

Первая строка таблицы соответствует уравнению:

.

Напомним, что на первом шаге симплекс-метода необходимо найти первоначальный опорный план (неотрицательное базисное решение системы), для этого умножим обе части уравнения на матрицу слева (она существует, так как по предположению невырожденная матрица). Получим

.

Полагая , найдем значения базисных переменных:

( единичная матрица m-го порядка).

Если при этом , то

является первоначальным опорным планом.

Эти преобразования системы ограничений соответствуют таблице:

		0

Вычислим значение целевой функции, соответствующее опорному плану, подставив в выражение (вторая строка таблицы). Получим

.

Рассматривая идею симплекс-метода, мы пришли к выводу, что опорный план является оптимальным, если в целевой функции, выраженной только через свободные переменные, все коэффициенты неотрицательны.

Чтобы проверить полученный опорный план на оптимальность, выразим целевую функцию через свободные переменные . Для этого умножим первую строку последней таблицы на и вычтем из второй строки, чтобы коэффициенты в строке при базисных неизвестных были равны 0. Получим таблицу:

0

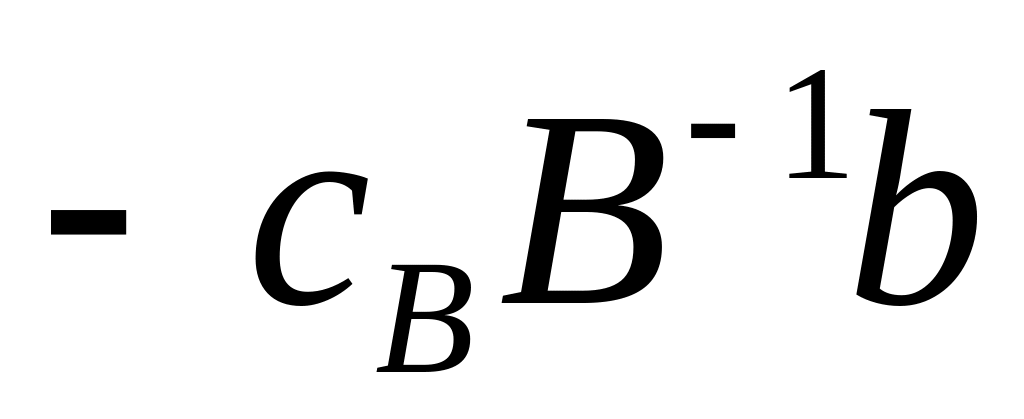
Обозначим через вектор, состоящий из коэффициентов при свободных неизвестных целевой функции. Согласно рассуждениям, проведенным в п. 6.1, опорное решение будет оптимальным, если Последняя строка таблицы соответствует значению функции:

В найденном опорном плане (при ) значение

.

Видим, что соответствующее значение находится в правом нижнем углу таблицы с противоположным знаком.

6.2.1. Алгоритм симплекс-метода

1. Запишем условия задачи:

в виде таблицы:

БП	х1	...	хn	Свободный член
	a11	...	a1n	b1
	...	...	...	...
	am1	...	amn	bm
Z	c1	...	cn	0	,

которую будем называть симплекс-таблицей. В левом столбце записываются базисные переменные (БП).

2. С помощью шагов Жордана–Гаусса найдем первоначальный опорный план, т.е. преобразуем таблицу так, чтобы система уравнений была приведена к базисному виду с неотрицательными свободными членами. При этом функция цели должна быть выражена через свободные неизвестные. Не нарушая общности, можно считать, что базисными переменными являются , тогда симплекс-таблица примет вид:

БП	x1	x2	…	xm	xm+1	…	xs	…	xn	Свободный член
x1	1	0	…	0	a′1,m+1	…	a′1,s	…	a′1,n	b′1
x2	0	1	…	0	a′2,m+1	…	a′2,s	…	a′2,n	b′2
…	…	…	…	…	…	…	…	…	…	…
xm	0	0	…	1	a′m,m+1	…	a′m,s	…	a′m,n	b′m
Z	0	0	…	0	r1	…	rs	…	rn–m	q
	Коэффициенты при базисных неизвестных				Вектор r коэффициентов при свободных неизвестных

В данной таблице , .

Полагая свободные неизвестные , получаем из таблицы неотрицательное базисное решение (опорный план)

.

3. Анализируем строку коэффициентов при свободных неизвестных, т.е. вектор в Z-строке.

Если , то соответствующее опорное решение является оптимальным, .

Если среди компонент вектора имеется хотя бы одна отрицательная, то полученный опорный план не является оптимальным. Необходимо перейти к новому опорному плану.

4. Для перехода к новому опорному плану выбираем максимальную по модулю отрицательную компоненту вектора , пусть это будет 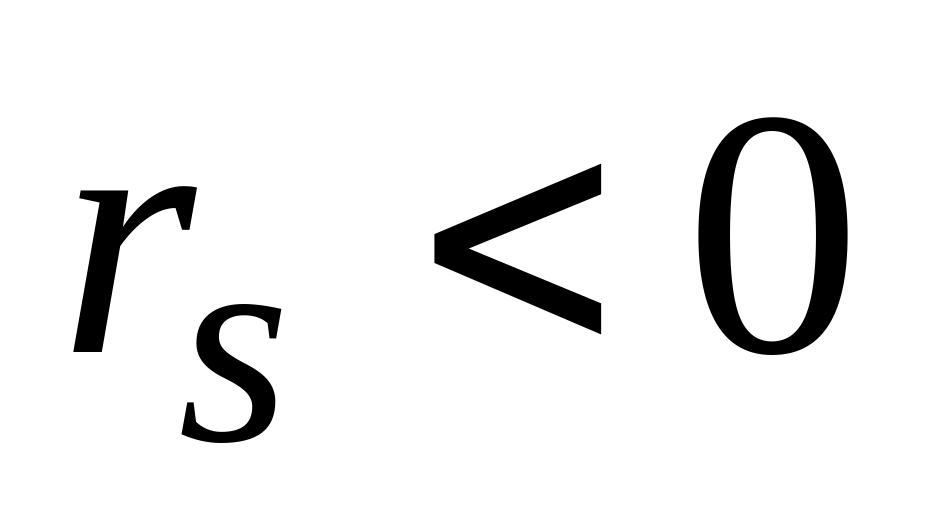. Анализируем коэффициенты s-го столбца матрицы системы ограничений.

Если все коэффициенты , то, как было сказано выше, задача не имеет решения из-за неограниченности целевой функции .

Если среди коэффициентов есть хотя бы один положительный, то s-столбец выбираем разрешающим и переходим к п. 5.

5. Для выбора разрешающей строки составляем неотрицательные отношения

и выбираем среди них наименьшее:

.

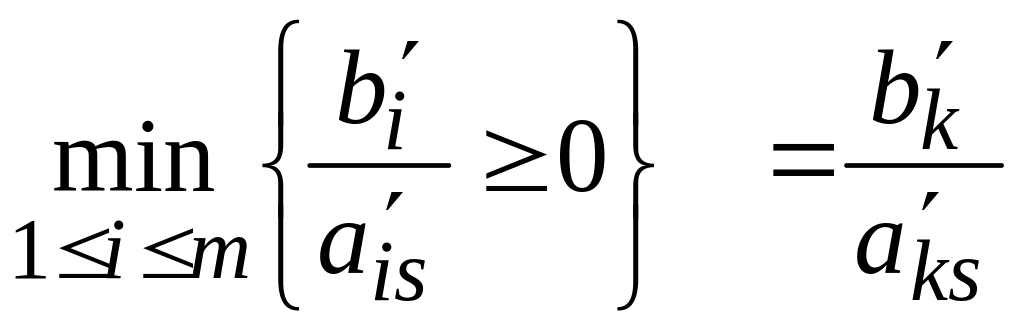Таким образом, определилась разрешающая k-я строка и разрешающий элемент .

6. Выполняем шаг преобразований Жордана–Гаусса с разрешающим элементом и переходим к п. 3.

Замечание. Если 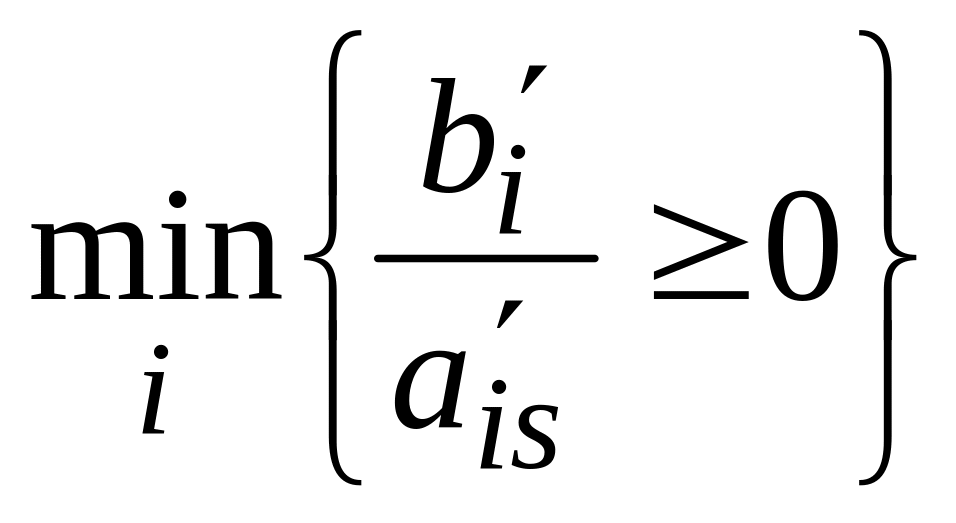достигается для нескольких строк, то за разрешающую строку можно принять любую из них, при этом в новом опорном плане значения некоторых базисных переменных станут равны нулю, т.е. получаем вырожденный опорный план.

Пункт 5 нуждается в дополнительном пояснении.