7.3. Симметричные двойственные задачи

Пусть модель исходной ЗЛП задана в стандартной форме:

(7.1)

Составим модель двойственной ЗЛП, используя правила, изложенные в п. 7.2.

Модель двойственной задачи примет вид:

(7.2)

Если ввести в рассмотрение матрицы:

,

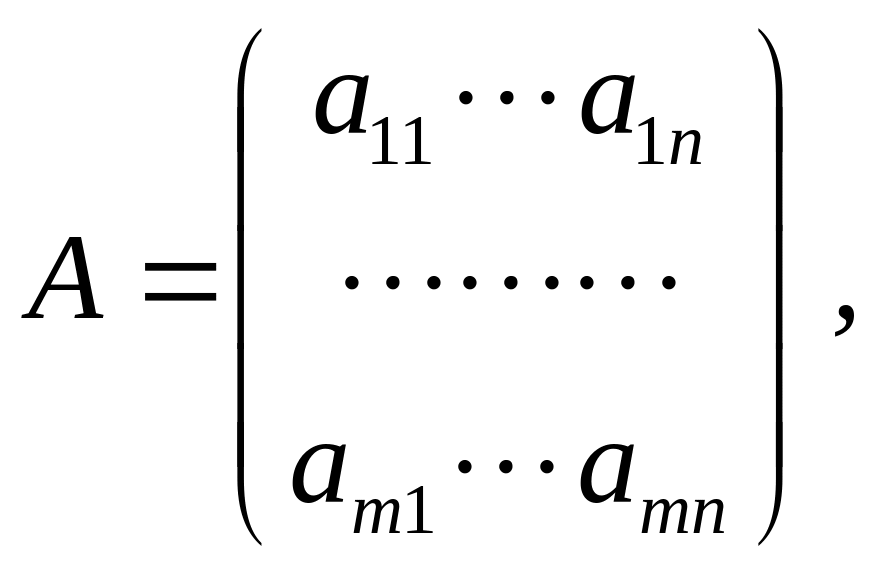
то пара симметричных двойственных задач в матричной форме примет вид:

Прямая задача

Двойственная задача

Пример 7.2. Составить двойственную задачу к следующей ЗЛП:

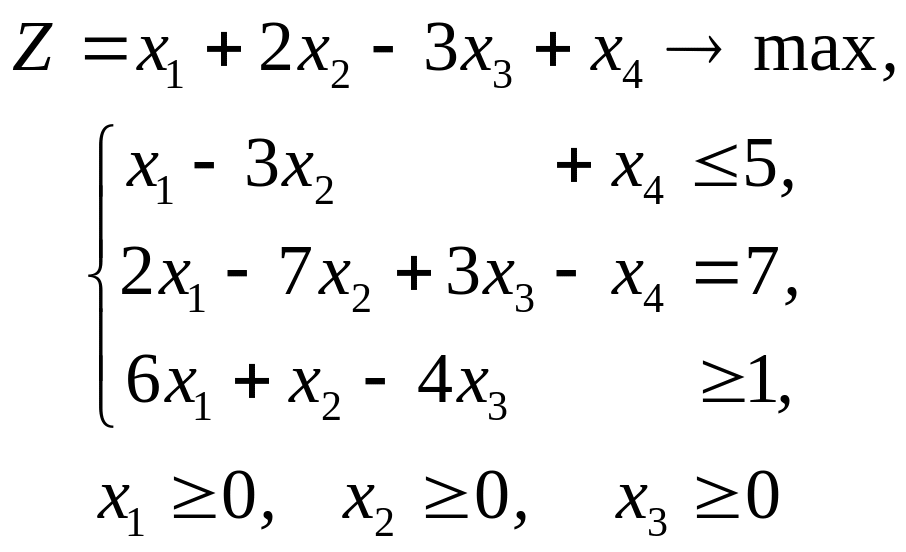
и показать взаимосопряженность полученной пары двойственных задач.

Решение. Прежде всего приведем модель к виду, для которого изложены правила построения двойственных задач.

Преобразуем третье ограничение, умножив обе части неравенства на –1 и изменив знак неравенства на противоположный:

В результате исходная задача примет вид:

(7.3)

Согласно правилам двойственная задача будет содержать три переменные (они записаны справа от ограничений), причем , так как соответствуют ограничениям-неравенствам исходной задачи, а у₂ является свободной переменной: у₂ 0 (у₂ соответствует ограничению-равенству исходной задачи).

Матрицей системы ограничений двойственной задачи является матрица, транспонированная к исходной:

.

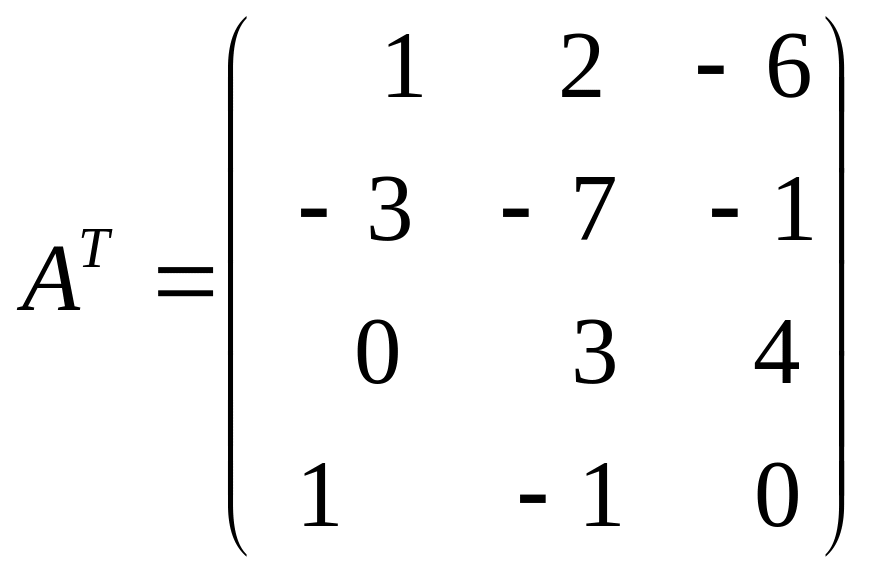Правыми частями системы ограничений двойственной задачи станут коэффициенты (1, 2, –3, 1) целевой функции исходной задачи.

Каждой неотрицательной переменной исходной задачи соответствует ограничение-неравенство того же смысла:

Свободной переменной х₄ соответствует ограничение-равенство:

х₄ 0 у₁ – у₂=1.

Коэффициентами целевой функции W двойственной задачи, которая (согласно правилам) минимизируется, становятся свободные члены системы ограничений исходной задачи.

Итак, математическая модель двойственной задачи примет вид:

(7.4)

Далее покажем взаимосопряженность полученной пары двойственных задач, т.е. покажем, что задача, двойственная к (7.4), совпадает с исходной (7.3).

Для этого прежде всего преобразуем модель (7.4) к виду:

Согласно правилам построения двойственных задач получим модель двойственной задачи:

Умножив обе части первых двух ограничений на –1 и введя функцию Z= –Z₁, получим эквивалентную ЗЛП:

которая совпадает с исходной.

Таким образом, показана взаимосопряженность пары двойственных задач, что позволяет считать одну из них (безразлично какую) исходной, а вторую – двойственной к ней.

Пример 7.3. Для задачи:

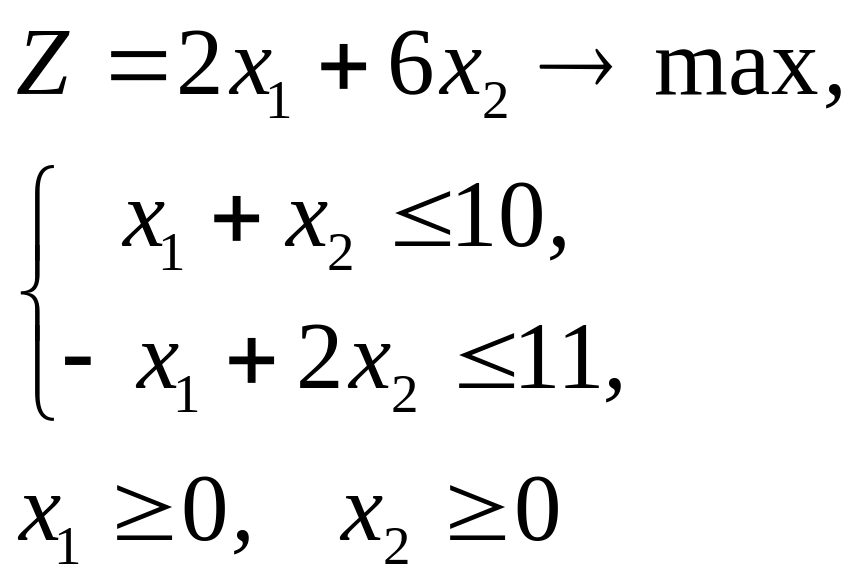
составить двойственную и найти решение обеих задач.

Решение. Двойственной является задача:

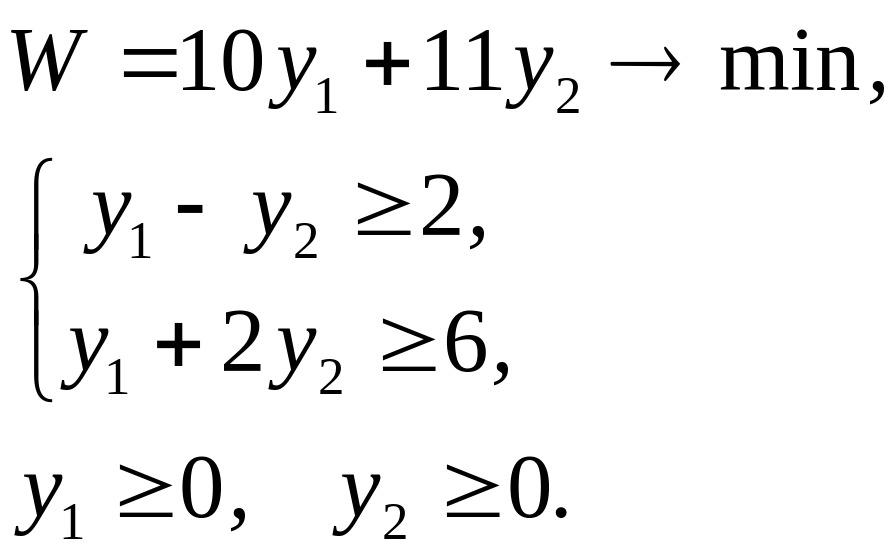
Как в исходной, так и в двойственной задаче число неизвестных равно двум. Следовательно, их решение можно найти графическим методом.

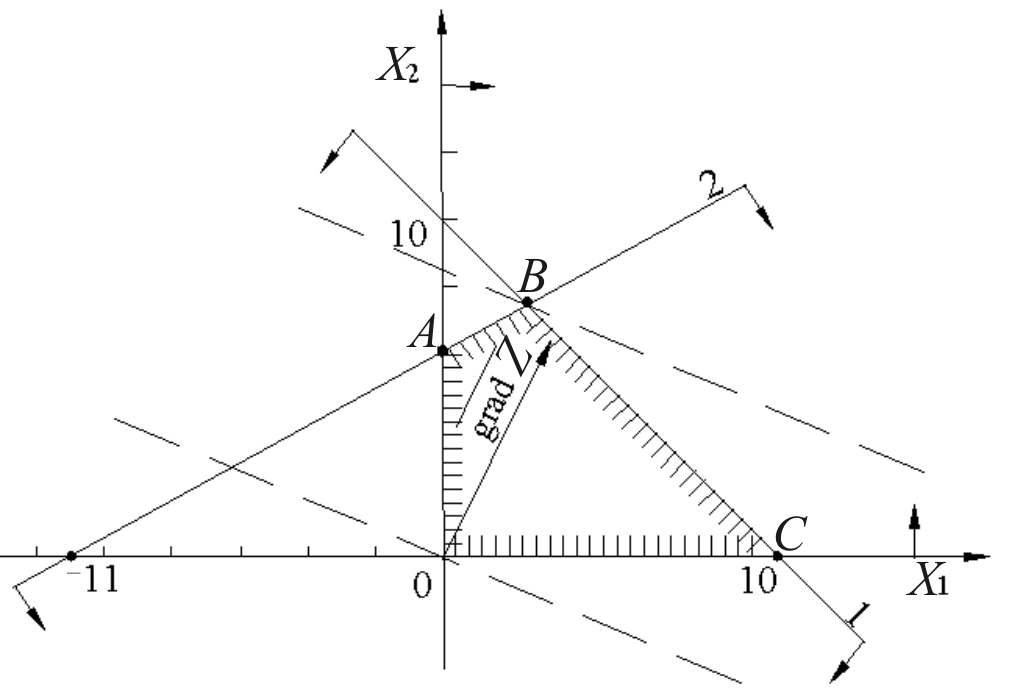
Рис. 7.1. достигается в точке B

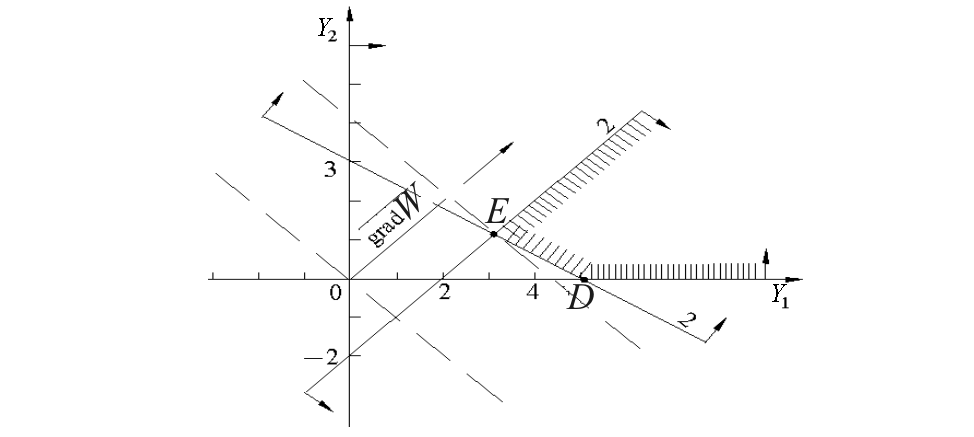Рис. 7.2. достигается в точке Е

Как видно из рис. 7.1, максимальное значение целевая функция исходной задачи принимает в точке В. Следовательно, Х^*=(3,7) является оптимальным планом, при котором Z_max=48.

В двойственной задаче (рис 7.2) ОДР не ограничена. Минимальное значение целевая функция двойственной задачи принимает в точке Е, т.е. и Таким образом, значения целевых функций исходной и двойственной задач при их оптимальных планах равны между собой.

Далее будет показано, что для любой пары двойственных задач, имеющих оптимальные решения, экстремальные значения целевых функций совпадают (Z_max=W_min).