Э.В. Киселева

С.И. Соловьева

математическое

программирование

(ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ)

НОВОСИБИРСК 2002

Э.В. Киселева

С.И. Соловьева

математическое

программирование

(ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ)

НОВОСИБИРСК 2002

Оглавление

Введение ……………………………………………………..				5
1.	Примеры экономических задач линейного программирования……..................			12
	1.1. Задача оптимального производственного планирования…………………………………………………...............			12
	1.2. Задача о смесях……………………………………......			13
	1.3. Задача о раскрое....…………………………………....			15
	1.4. Транспортная задача ……………………………….....			16
	1.5. Вопросы для самопроверки ……………………….....			18
2.	Некоторые сведения из линейной алгебры..			19
	2.1. Основные понятия и теоремы …………………….....			19
	2.2. Решение систем линейных алгебраических уравнений методом ЖорданаГаусса..................……………........			20
3.	Различные формы модели задачи линейного программирования …................….			26
	3.1. Формулировка основной задачи линейного программирования …………………………….…………….............			26
	3.1.1. Общая форма модели ………………………........			26
	3.1.2. Стандартная форма модели ………………..........			26
	3.1.3. Каноническая форма модели ……………...........			27
	3.2. Понятие допустимого решения, области допустимых решений, оптимального решения задачи линейного программирования …….......................................................…..			28
	3.3. Переход от задачи минимизации целевой функции к задаче максимизации ……………………………............			28
	3.4. Переход от одной формы модели задачи линейного программирования к другой.................................................			29
			3.4.1. Переход к канонической форме модели ….....	29
			3.4.2. Переход от канонической формы модели задачи линейного программирования к стандартной........	32
	3.5. Выпуклые множества …………………….……….......			34
4.	Графический метод решения ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ …..................….….			36
	4.1. Геометрическая интерпретация множества решений линейного неравенства ……………………………............			36
	4.2. Геометрическая интерпретация множества решений системы линейных неравенств …….……………...............			37
	4.3. Вопросы для самопроверки ………………………......			46
5.	Свойства допустимых планов ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. Опорный план..			47
6.	Симплекс-метод …………………………..................			51
	6.1. Идея симплекс-метода ……………………………......			51
	6.2. Алгебра симплекс-метода ………………………….....			55
		6.2.1. Алгоритм симплекс-метода ……………….......		58
		6.2.2. Выбор разрешающей строки в симплексных преобразованиях ……………………………...............		61
		6.2.3. Альтернативный оптимум ………………….....		62
		6.2.4. Признак неограниченности целевой функции..		63
	6.3. Понятие о вырождении …………………………….....			65
	6.4. Вопросы для самопроверки ………………………......			76
	6.5. Индивидуальное задание ……………...........................			77
	6.6. Задачи для самостоятельной работы …….………......			85
7.	Двойственность в линейном программировании ………………......………………………………			88
	7.1. Пример двойственных задач линейного программирования………………….. …………………....…………….			88
	7.2. Правила построения двойственных задач ……….......			90
	7.3. Симметричные двойственные задачи ……………......			92
	7.4. Основные теоремы двойственности ……………........			98
	7.5. Анализ устойчивости двойственных оценок …….....			115
	7.6. Вопросы для самопроверки ……………………….....			122
	7.7. Индивидуальное задание ……….........................…….			122
ЗАКЛЮЧЕНИЕ………………………………………………….				127
Библиографический список ………………………...				128
Приложение. Применение программы Excel к решению задач линейного программирования ………………………….				130

В мире не происходит ничего,

в чем не был бы виден

смысл какого-нибудь

максимума или минимума.

Л. Эйлер

ВВЕДЕНИЕ

Многие задачи, с которыми сталкивается человек в своей практической деятельности, допускают различные варианты решения. Человек всегда стремился отыскать наилучший вариант с учетом ограничений, налагаемых на природные, экономические, технические возможности. Долгое время при этом он руководствовался лишь здравым смыслом, опытом, интуицией.

Однако с развитием общества произошло резкое увеличение размеров производства, появилась необходимость решать задачи планирования и управления, выработки прогнозов на будущее и др. Увеличился объем информации, которую необходимо учитывать при решении таких задач, необходимо учитывать также связи между отдельными, казалось бы, не связанными между собой явлениями (промышленное производство и загрязнение окружающей среды, запасы ценных промысловых рыб и химизация сельского хозяйства и т.д.).

С другой стороны, возникновение быстродействующих вычислительных машин позволило решать задачи, требующие огромного объема вычислений, привлекать математический аппарат к решению задач, решаемых ранее «на глазок», создавать принципиально новые, численные методы решения задач.

Так в XX в. появились новые математические дисциплины, в числе которых математическое программирование.

Математическое программирование – это раздел математики, занимающийся анализом многомерных экстремальных задач управления и планирования и разработкой теории и численных методов их решения. Иными словами, математическое программирование занимается решением задач нахождения максимума или минимума функции многих переменных с ограничениями на область изменения этих переменных.

Наиболее разработанной в настоящие время составной частью математического программирования является линейное программирование.

Впервые постановка задачи линейного программирования в виде предложения по составлению оптимального плана перевозок, позволяющего минимизировать суммарный километраж, дана в работе советского математика А.Н. Толстого (1930). В 1931 г. венгерский математик Б. Эгервари рассмотрел математическую постановку и решил задачу, имеющую название «проблема выбора», метод решения которой получил название венгерский метод. В 1939 г. советский ученый Л.В. Канторович указал общий метод (метод разрешающих множителей) решения задач, связанных с составлением оптимального плана при организации производственных процессов (в связи с решением задачи оптимального распределения работы между станками фанерного треста в Ленинграде). Он же совместно с М.К. Гавуриным в 1949 г. разработал метод потенциалов, используемый при решении транспортных задач. В последующих работах Л.В. Канторовича, В.С. Немчинова, В.В. Новожилова, А.Л. Лурье, А.Г. Аганбегяна, Д.Б. Юдина, Е.Г. Гольштейна и других математиков и экономистов получили дальнейшее развитие как математическая теория линейного и нелинейного программирования, так и приложение ее методов к исследованию различных экономических проблем.

В 1949 г. американским математиком Дж. Данцигом (G.B. Dantzig) был опубликован основной метод решения задач линейного программирования  симплекс-метод. Термин «линейное программирование» впервые появился в 1951 г. в работах Дж. Данцига и Т. Купманса.

При всем многообразии содержания конкретных задач решение каждой задачи проходит последовательно следующие основные этапы:

1. Постановка задачи.

2. Построение (составление) математической модели.

3. Выбор метода решения и решение задачи.

4. Проверка полученного решения на его адекватность изучаемому явлению и корректировка модели в случае необходимости.

5. Реализация найденного решения на практике.

Остановимся подробнее на втором этапе.

Математическая модель является абстрактным отображением реального процесса (явления) и в меру своей абстрактности может его характеризовать более или менее точно.

В построении математической модели можно выделить следующие моменты:

1. Выбор неизвестных величин Х = (х₁,…, х_n), воздействуя на которые можно изменять поведение изучаемого процесса. Их называют переменными, управляемыми параметрами, планом, стратегией и т.д.

2. Необходимо выделить цель (максимизация прибыли, минимизация затрат и др.) функционирования изучаемого процесса и записать ее в виде математической функции от выбранных переменных. Такая функция называется целевой (функция цели, критерий оптимальности, критерий качества, показатель эффективности и т.д.) и позволяет, изменяя значения управляемых параметров x₁,…, x_n, выбрать наилучший вариант из множества возможных. Будем обозначать функцию цели Z = f (X).

3. Запись в виде математических соотношений (уравнений, неравенств) условий, налагаемых на переменные. Эти соотношения называют ограничениями, они могут вытекать, например, из ограниченности ресурсов. Совокупность всех ограничений составляет область допустимых решений (ОДР). Будем обозначать ее буквой D (X 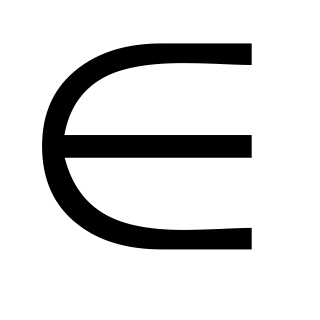D).

При таких обозначениях модель задачи математического программирования примет вид:

или в развернутом виде:

найти план доставляющий экстремальное значение целевой функции Z, т.е.

при ограничениях:

Из экономических или физических соображений на некоторые компоненты плана задачи, как правило, налагаются условия неотрицательности: