Опорный план. Теорема о соответствии опорного плана вершине многогранника допустимых планов

Рассмотрим ЗЛП в канонической форме:

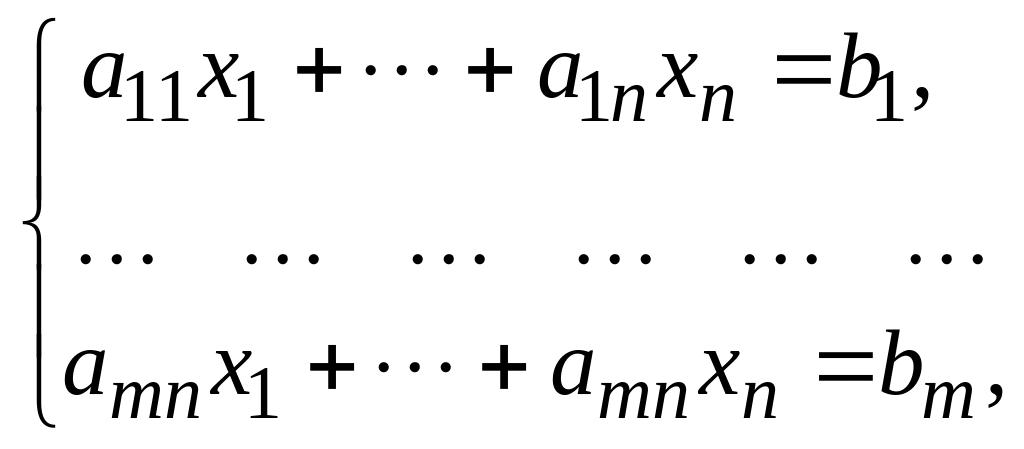
Предположим, что число линейно независимых уравнений системы ограничений равно m (m<n). Методом Жордана–Гаусса приведем систему к базисному виду:

(Не ограничивая общности, можно считать, что базисными переменными являются .)

Очевидно, базисное решение системы имеет вид:

Определение 5.1. Неотрицательное базисное решение системы ограничений ЗЛП называется опорным решением (опорным планом) ЗЛП.

Из определения следует, что:

1. если то соответствующее базисное решение является опорным решением ЗЛП;

2. число положительных координат опорного плана не может превышать m.

Определение 5.2. Опорный план называется невырожденным, если число его положительных компонентов равно m, и вырожденным в противном случае.

Теорема 5.4. Вектор Х является опорным планом ЗЛП тогда и только тогда, когда Х – вершина многогранника допустимых планов.

Итак, для нахождения оптимального решения ЗЛП достаточно исследовать вершины выпуклого многогранника допустимых решений. В этом и состоит основная идея симплекс-метода решения ЗЛП.

6. Симплекс-метод

На основании свойств ЗЛП, рассмотренных в предыдущей главе, можно сделать следующие выводы.

Если решение ЗЛП существует, то оно достигается хотя бы в одной вершине (опорном решении) многогранника допустимых решений, следовательно, поиск оптимального решения необходимо осуществлять среди вершин многогранника (опорных решений).

Однако при больших и перебор всех вариантов практически нереален. Для решения ЗЛП был предложен симплекс-метод, разработанный в 1947–49 гг. американским математиком Дж. Данцигом. Идея симплекс-метода состоит в целенаправленном переборе вершин многогранника допустимых решений (опорных планов) в направлении «улучшения» значений целевой функции.

Замечание. «Симплекс» в переводе с латинского значит «простейший». В многомерной геометрии симплексом называется геометрическое место точек, удовлетворяющих условиям:

, .

При малой размерности симплексом является точка, отрезок, треугольник, тетраэдр. Первая задача, решенная симплекс-методом, имела в качестве многогранника допустимых решений именно симплекс.

6.1. Идея симплекс-метода

Рассмотрим идею симплекс-метода на конкретном примере.

Пример 6.1.

Решение. Найдем первоначальное опорное (допустимое базисное) решение.

Чтобы получить базисное решение, необходимо систему линейных уравнений привести к базисному виду, приравняв свободные неизвестные нулю.

Замечаем, что система уравнений уже приведена к базисному виду ( базисные неизвестные, свободные неизвестные).

Положив получаем первоначальное базисное решение

, причем .

Очевидно, это базисное решение является опорным, так как все

Итак, первый этап симплекс-метода закончен.

Выясним теперь, является ли опорное решение оптимальным. Для этого рассмотрим функцию цели . Обратим внимание на тот факт, что она выражена только через свободные неизвестные и .

Возникает вопрос, можно ли уменьшить значение целевой функции за счет перехода к новому опорному решению, в котором в базис будет введена одна из свободных переменных: либо , либо , либо . Очевидно, введение в базис переменной нецелесообразно, так как коэффициент при ней в функции цели равен +7 и увеличение этой переменной на единицу приведет к увеличению значения функции на 7 единиц. А вводя в базис или , мы можем уменьшить значение Z (поскольку коэффициенты при них отрицательны). Для определенности введем в базис , т.е. ту из свободных переменных, которая имеет наибольший по модулю отрицательный коэффициент .

Если бы все коэффициенты в функции Z были положительны, то уменьшить значение Z было бы невозможно введением в базис любой из свободных переменных и, следовательно, найденное опорное решение являлось бы оптимальным.

Итак, вводим в базис.

Далее необходимо выяснить, какую из базисных переменных ( или ) можно вывести из базиса, т.е. сделать равной нулю.

Так как и остаются свободными переменными, т.е. , то система ограничений примет вид:

(*)

Если вывести из базиса , т.е. положить , то получим , , что недопустимо ( , ).

Если вывести из базиса , то получим , , , что соответствует опорному плану:

, .

В этом случае базисные переменные, а свободные переменные. Видим, что при переходе к новому опорному плану значение целевой функции уменьшилось:

.

Для ответа на вопрос, является ли опорное решение оптимальным, выразим функцию цели через свободные неизвестные .

С помощью второго уравнения системы ограничений мы установили, что переменная вводится в базис вместо переменной , поэтому, выразив из второго уравнения

и подставив его в целевую функцию , получим

.

Исключив из первого уравнения, перейдем к задаче:

Здесь базисные, а свободные переменные.

Замечаем, что в целевую функцию свободная переменная входит с отрицательным коэффициентом –1, поэтому согласно предыдущим рассуждениям опорный план не является оптимальным. Достаточно ввести в базис свободную переменную , как значение функции уменьшится. Очевидно, при этом вывести из базиса можно только переменную с помощью первого уравнения системы ограничений.

Разделив первое уравнение на 6, выразив из него и подставив его в функцию цели Z, получим задачу:

,

где базисные переменные, а свободные переменные. Положив , получим опорный план

, причем .

Очевидно, что полученный опорный план является оптимальным, т.е.

,

Действительно, так как все коэффициенты при свободных переменных неотрицательны в функции цели , то введение в базис любой из них не приведет к уменьшению значения целевой функции.

Замечание. Если найденный опорный план не является оптимальным (в целевую функцию входит какая-либо свободная переменная с отрицательным коэффициентом) и все коэффициенты -го столбца в системе ограничений, соответствующего этой переменной, неположительны, то целевая функция не ограничена снизу. В этом случае ЗЛП не имеет решения.

Поясним это на рассмотренном примере 6.1. Пусть, например, в системе (*) коэффициенты при переменной , которую хотим ввести в базис, в обоих уравнениях отрицательны:

Откуда

Очевидно, увеличение значения переменной приведет к увеличению значений переменных и и мы никогда не получим нулевых значений и , т.е. и нельзя вывести из базиса. Но при неограниченном увеличении значение целевой функции будет неограниченно уменьшаться ( ), т.е. оптимальное решение не существует в этом случае по причине неограниченности снизу функции .