3.3. Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции Z легко может быть сведена к задаче максимизации функции Z₁ при тех же ограничениях путем введения функции

.

Обе задачи имеют одно и то же решение и при этом

.

Проиллюстрируем этот факт графически на примере функции одной переменной:

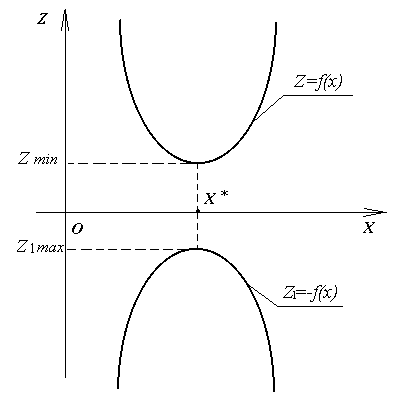
Рис. 3.1. и достигается в точке

Функция представляет собой зеркальное отражение функции относительно оси ОХ, ее максимум достигается в той же точке , что и минимум функции . Очевидно, имеет место соотношение .

3.4. Переход от одной формы модели задачи линейного программирования к другой

3.4.1. Переход к канонической форме модели

Пусть исходная ЗЛП задана в стандартной форме

, (3.1)

(3.2)

. (3.3)

Преобразуем ее к каноническому виду. Для того чтобы неравенства типа преобразовать в равенства, к их левым частям прибавим дополнительные (балансовые) неотрицательные переменные , после чего система ограничений примет вид:

Дополнительные (балансовые) переменные вводятся в целевую функцию с коэффициентами, равными нулю.

Каноническая форма модели примет вид:

(3.4)

, (3.5)

. (3.6)

Теорема 3.1. Каждому решению ( ) неравенства соответствует единственное решение уравнения и неравенства , и наоборот.

Из данной теоремы следует эквивалентность систем ограничений исходной стандартной формы модели задачи и полученной канонической формы. А так как дополнительные переменные входят в целевую функцию с коэффициентами, равными нулю, то значения целевых функций (3.1) и (3.4) при соответствующих допустимых решениях и одинаковы. Отсюда следует, что целевые функции (3.1) и (3.4) на множестве соответствующих допустимых решений достигают экстремальных значений одновременно. Оптимальному решению ( ) задачи (3.1)–(3.3) соответствует оптимальное решение задачи (3.4)–(3.6), т.е. исходная модель и ее каноническая форма эквивалентны.

Пример. При производстве двух видов изделий (А и В) предприятие использует 4 вида ресурсов. Нормы расхода ресурсов на производство единицы продукции, объем ресурсов, а также прибыль от реализации единицы продукции приведены в таблице:

Вид ресурса	Нормы затрат ресурсов		Объем ресурса
	А	В
1	2	3	20
2	3	1	15
3	4	0	16
4	0	3	12
Прибыль	5	3

Определить оптимальный план производства продукции, обеспечивающий предприятию максимальную прибыль.

Составить математическую модель задачи и привести ее к каноническому виду.

Решение. Обозначим через план выпуска продукции. Модель задачи примет вид:

Модель записана в стандартной форме.

Перейдем к модели в каноническом виде. Введем балансовые неотрицательные переменные , которые прибавим к левым частям ограничений-неравенств. В целевую функцию все дополнительные переменные введем с коэффициентами, равными нулю. Получим каноническую форму модели:

Отметим экономический смысл дополнительных переменных. Очевидно,

,

т.е. дополнительная переменная показывает величину неиспользованного i-го ресурса .