
- •Зміст дисципліни за темами
- •Тема 1. Концептуальні аспекти економетричного моделювання економіки
- •Тема 2. Принципи побудови економетричних моделей. Парна та множинна лінійна регресія
- •Тема 3: Моделі множинних регресій, що зводяться до лінійних
- •Тема: Економіко – математичне моделювання
- •2. Математична модель економічного об’єкту
- •Критерії вибору „хорошої моделі”:
- •За характером застосування методів дослідження виділяються:
- •2. Об'єкт, предмет, мета і завдання економетрії
- •3. Основні етапи економетричного аналізу
- •4. Економічні задачі, які розв'язують за допомогою економетричних методів
- •5. Основні етапи зародження та розвитку економетрії
- •Тема: Регресійні моделі
- •1. Поняття регресії
- •3. Парна лінійна регресія
- •4. Теоретична і розрахункова моделі
- •5. Метод найменших квадратів – метод розрахунку параметрів моделі.
- •6. Дисперсійний аналіз моделі
- •Приклад виконання типового завдання
- •1. Економічна постановка задачі
- •2. Геометричне зображення залежності між досліджуваними показниками
- •3. Оцінювання параметрів парної лінійної регресії
- •4. Розрахунок коефіцієнта детермінації та парної кореляції.
- •5. Перевірка достовірності побудови моделі на основі статистичних критеріїв
- •5. Визначення стандартних похибок та довірчих інтервалів для оцінок параметрів моделі
- •6. Точковий та інтервальний прогноз на основі побудованої моделі.
- •Тема: Загальна лінійна економетрична модель
- •1. Множинна лінійна регресія
- •2. Передумови застосування метода найменших квадратів
- •3. Дисперсійний і регресійний аналіз моделей
- •4. Точковий та інтервальльний прогноз
- •5. Перевірка якості та статистичної значущості моделі
- •Завдання №1 на самостійну роботу
- •1). Побудувати економетричну модель залежності між факторами за допомогою функції «линейн»:
- •Тема: Нелінійні моделі
- •Степенева (поліноміальна ) модель
- •2. Гіперболічна модель
- •3. Показникові моделі
- •4. Виробнича функція Кобба – Дугласа
- •Завдання №2 на самостійну роботу
- •Тема: Фіктивні змінні в регресійних моделях
- •1. Необхідність використання фіктивних змінних
- •2. Моделі ancova
- •2.1. Ancova - Модель при наявності у фіктивної змінної двох альтернатив
- •2.2. Моделі ancova за наявності у якісних змінних більш двох альтернатив
- •3. Використання фіктивних змінних у сезонному аналізі
- •Завдання № 3* на самостійну роботу Розрахувати моделі із фіктивними змінними :
- •Дослідити розраховану модель на значущість. Тема: Мультиколінеарність факторів моделі
- •Поняття мультиколінеарності
- •Основні наслідки мультиколінеарності:
- •Дослідження наявності мультиколінеарності
- •Ознаки мультиколінеарності
- •Алгоритм Фаррара – Глобера
- •Завдання №4 на самостійну роботу
- •Тема: Гетероскедастичність моделі
- •1. Поняття гетероскедастнчності та її наслідки
- •2. Перевірка гетероскедастичності
- •Тема: Автокореляція відхилень (залишків)
- •1. Поняття автокореляції та її наслідки
- •Перевірка наявності автокореляції
- •Завдання № 5 на самостійну роботу
Приклад виконання типового завдання
1. Економічна постановка задачі
На підставі даних про рівень прибутку і обсяг інвестицій (у грошових одиницях) побудувати економетричну модель залежності між економічними показниками. Розрахувати прогнозне значення залежної змінної та довірчі інтервали прогнозу. Дані наведено в таблиці:
-
Період часу
Х, обсяг інвестицій (тис. грн.)
Y, прибуток
(тис. грн.)
Січень
60,000
38,000
Лютий
63,000
40,000
Березень
56,000
37,000
Квітень
64,000
41,000
Травень
67,000
43,000
Червень
56,000
38,000
Липень
70,000
45,000
Серпень
68,000
44,000
Вересень
73,000
47,000
Жовтень
77,000
50,000
Листопад
75,000
48,000
2. Геометричне зображення залежності між досліджуваними показниками
Зображуємо «хмару розсіювання» – кореляційне поле – множину точок із координатами ( х; у) у специфічній системі координат. .
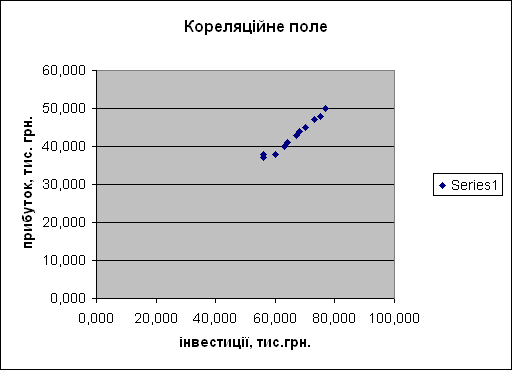
Рис.1.2
Побудова «Хмари розсіювання» :
“Точечные диаграммы”;
“Диапазон”;
Массивы (Х; Y).
Розташування точок на координатній площині свідчить, що зв'язок між даними показниками близький до лінійного.
3. Оцінювання параметрів парної лінійної регресії
Для оцінки параметрів парної лінійної регресії використовується метод найменших квадратів.
Специфікація
моделі. Розглядається зв'язок між двома
показниками – рівнем прибутку і обсягом
інвестицій (тис. грн.), отже маємо парну
регресію. Позначимо залежну змінну –
прибуток (тис. грн.) через Y,
а незалежний фактор -
обсяг інвестицій (тис.
грн.) через Х.
На основі геометричного
зображення залежності між досліджуваними
показниками можемо припустити, що
зв'язок буде достатньо адекватно
відображатись лінійною залежністю.
Отже, теоретична модель матиме вигляд:
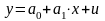 ,
а емпіричне рівняння залежності матиме
вигляд:
,
а емпіричне рівняння залежності матиме
вигляд:
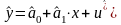 .
.
Система нормальних рівнянь для знаходження параметрів парної лінійної регресії має вигляд:
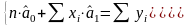
Знаходження параметрів парної лінійної регресії матричним способом:
M
=
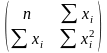 , В =
, В =
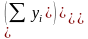
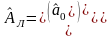
Використання
стандартних функцій «Excel»
для розрахунку коефіцієнтів моделі
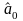 ,
,
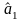 матричним способом:
матричним способом:
-
виділити масив матриці результату: (
m
 n)•
( n
k)
= ( m
k),
де
n)•
( n
k)
= ( m
k),
де
т – кількість рядків першої матриці,
п - кількість стовпчиків першої матриці і рядків другої матриці,
k - кількість стовпчиків другої матриці
- fx: «Математические функции» → “МОБР”, “МУМНОЖ” ;
- Комбінація кнопок: F2+ Ctrl + Shift + Enter
Розрахунки зручно представити у вигляді таблиці (табл.1.4):
-
x
y
x∙y
x2
60,000
38,000
2280,000
3600,000
63,000
40,000
2520,000
3969,000
56,000
37,000
2072,000
3136,000
64,000
41,000
2624,000
4096,000
67,000
43,000
2881,000
4489,000
56,000
38,000
2128,000
3136,000
70,000
45,000
3150,000
4900,000
68,000
44,000
2992,000
4624,000
73,000
47,000
3431,000
5329,000
77,000
50,000
3850,000
5929,000
75,000
48,000
3600,000
5625,000
729,000
471,000
31528,000
48833,000
Сума
хс = 66,27
ус = 42,82
Відповідні матриці системи нормальних рівнянь:
М
=
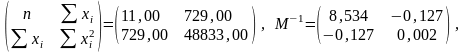 ,
,
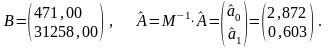

Розрахункове рівняння регресії Ŷ = 2,872 + 0,603∙Х + u^.
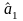 =
0,603 означає, що збільшення
рівня інвестицій на 1
тис. грн. збільшить очікуваний прибуток
на 0,603
тис.грн.
=
0,603 означає, що збільшення
рівня інвестицій на 1
тис. грн. збільшить очікуваний прибуток
на 0,603
тис.грн.
Коефіцієнт еластичності:
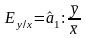 =
0,603 ∙ 66,27
/ 42,82 =
0,903 свідчить, що збільшення рівня
інвестицій на 1% призведе
до збільшення очікуваного прибутку
на 0,903%.
=
0,603 ∙ 66,27
/ 42,82 =
0,903 свідчить, що збільшення рівня
інвестицій на 1% призведе
до збільшення очікуваного прибутку
на 0,903%.
Побудова графіка моделі (рис.1.3):
- “Точечные диаграммы”
- “Диапазон”
-
Массивы (Х; Y) +
Ctrl
массив
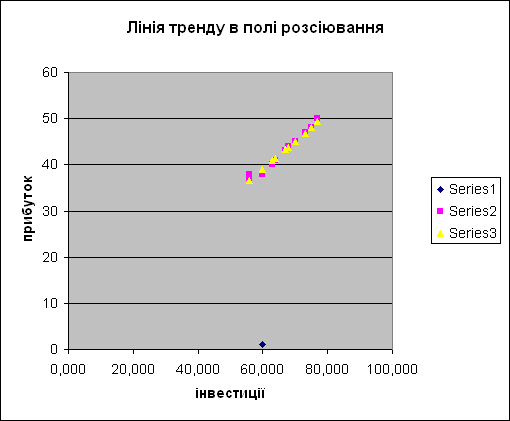
Рис.1.3. Графік лінійної моделі у кореляційному полі
