Алгоритм Фаррара – Глобера
Цей алгоритм використовує три види статистичних критеріїв:
За критерієм “χ - квадрат” перевіряється мультиколінеарність усього масиву факторів.
За F критерієм перевіряється залежність кожного фактора з рештою факторів.
За критерієм Ст'юдента t перевіряється кожна пара факторів.
Вразі існування мультиколінеарності факторів доцільно звернути увагу і на специфікацію моделі. Іноді заміна однієї функції іншою, яка не суперечить інформації, дозволяє усунути мультиколінеарність.
У випадку дослідження економетричних моделей із великого кількісно факторів, коли не вдається позбутися мультиколінеарності, параметри моделі оцінюють методом головних компонент .
Приклад дослідження наявнoстi мультиколінеарності у масиві змінних
Крок 1: нормалізація пояснюючих змінних
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
X1 н |
X2 н |
X3н |
X4 н |
X5 н |
63,00 |
240,00 |
31,00 |
15,00 |
8,00 |
-1,06 |
-1,23 |
-1,81 |
1,65 |
-1,30 |
64,00 |
242,00 |
36,00 |
14,30 |
8,50 |
-0,94 |
-1,08 |
-1,10 |
1,44 |
-1,10 |
61,00 |
235,00 |
34,00 |
12,00 |
7,00 |
-1,30 |
-1,62 |
-1,39 |
0,74 |
-1,71 |
62,00 |
239,00 |
35,00 |
12,80 |
9,00 |
-1,18 |
-1,31 |
-1,24 |
0,99 |
-0,89 |
65,00 |
250,00 |
37,00 |
13,00 |
10,00 |
-0,82 |
-0,45 |
-0,96 |
1,05 |
-0,49 |
66,00 |
250,00 |
39,00 |
12,50 |
11,00 |
-0,70 |
-0,45 |
-0,68 |
0,90 |
-0,08 |
68,00 |
255,00 |
41,00 |
11,00 |
9,50 |
-0,45 |
-0,06 |
-0,40 |
0,44 |
-0,69 |
63,00 |
248,00 |
42,00 |
11,50 |
12,00 |
-1,06 |
-0,61 |
-0,26 |
0,59 |
0,33 |
71,00 |
253,00 |
46,00 |
10,00 |
10,00 |
-0,09 |
-0,22 |
0,31 |
0,14 |
-0,49 |
72,00 |
255,00 |
46,00 |
9,00 |
14,00 |
0,03 |
-0,06 |
0,31 |
-0,16 |
1,14 |
73,00 |
260,00 |
47,00 |
8,00 |
12,50 |
0,16 |
0,33 |
0,45 |
-0,46 |
0,53 |
75,00 |
263,00 |
49,00 |
7,50 |
12,00 |
0,40 |
0,56 |
0,73 |
-0,61 |
0,33 |
76,00 |
262,00 |
48,00 |
6,50 |
10,00 |
0,52 |
0,49 |
0,59 |
-0,92 |
-0,49 |
81,00 |
270,00 |
51,00 |
6,00 |
11,00 |
1,13 |
1,11 |
1,01 |
-1,07 |
-0,08 |
78,00 |
255,00 |
50,00 |
6,20 |
12,00 |
0,76 |
-0,06 |
0,87 |
-1,01 |
0,33 |
83,00 |
275,00 |
52,00 |
5,80 |
15,00 |
1,37 |
1,50 |
1,15 |
-1,13 |
1,55 |
84,00 |
276,00 |
51,00 |
5,50 |
15,50 |
1,49 |
1,58 |
1,01 |
-1,22 |
1,75 |
86,00 |
276,00 |
54,00 |
5,00 |
14,50 |
1,73 |
1,58 |
1,43 |
-1,37 |
1,35 |
1291,00 |
4604,00 |
789,00 |
171,60 |
201,50 |
сума |
|
|
|
|
Хсер= «СРЗНАЧ» σ = «СТАНДОТКЛОН»
Хсер1 = 71,72 σ1=8,23
Хсер2 = 255,78 σ2=12,80
Хсер3 =43,83 σ3=7,10
Хсер4 = 9,53 σ4=3,31
Хсер5 =11,1 σ5=2,46
Х
н=
«НОРМАЛИЗАЦИЯ» =
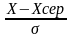
Крок 2: знаходження кореляційної матриці R нормалізованих факторів.
1 |
0,90 |
0,89 |
-0,89 |
0,74 |
0,90 |
1 |
0,87 |
-0,84 |
0,78 |
0,89 |
0,87 |
1 |
-0,91 |
0,77 |
-0,89 |
-0,84 |
-0,91 |
1 |
-0,71 |
0,74 |
0,78 |
0,77 |
-0,71 |
1 |
=
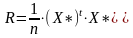det R = 0,0001
Крок
3: Визначення критерію
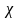2
відповідає за виявлення мультиколінеарності
в усьому масиві змінних.
=
93,22
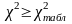= 23,21 в
масиві змінних існує мультиколінеарність.
Крок
4: Визначення оберненої
матриці.
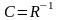
22,40 |
-13,10 |
1,00 |
10,80 |
0,54 |
-13,10 |
15,69 |
-4,46 |
-4,46 |
-2,43 |
1,00 |
-4,46 |
22,61 |
16,41 |
-3,14 |
10,80 |
-4,46 |
16,41 |
21,74 |
-1,79 |
0,54 |
-2,43 |
-3,14 |
-1,79 |
3,85 |
С=
F1= |
69,54 |
F2= |
47,75 |
F3= |
70,22 |
F4= |
67,41 |
F5= |
9,26 |
Ft |
3,18 |
Крок
5: Обчислення F-критеріїв
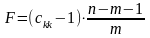
F > F табл. - зв'язок між кожною змінною з усіма іншими є істотним, тобто кожна змінна є мультиолінеарною із іншими.
Крок
6: знаходження частинних
коефіцієнтів кореляції
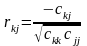
r12 = 0,70, r13 = 0,04 , r14 = 0,49, r15 = 0,06;
r23 = 0,24, r24 = - 0,24, r25 = - 0,31;
r34 = - 0,74, r35 = - 0,39;
r45 = 0,20
t12 |
3,52 |
t13 |
0,16 |
t14 |
2,02 |
t15 |
0,21 |
|
|
t23 |
0,88 |
t 24 |
0,90 |
t 25 |
1,18 |
|
|
|
|
t34 |
3,97 |
t 35 |
1,55 |
|
|
|
|
|
|
t45 |
0,72 |
tтабл |
2,16 |
|
|
|
|
|
|
Крок 7: обчислення Т-критеріїв
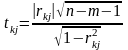
t12, t34 > t табл - попарні зв’язки між відповідними змінними є статистично значущими, тобто ці змінні є попарно мультиколінеарними.