Перша інтерполяційна формула Ньютона

Як видно з цього прикладу кінцеві різниці вищих порядків в нижній частині таблиці зникають. Тому приведена формула не може бути застосована для х в цій частині таблиці. Тут працює друга інтерполяційна формула Ньютона, яка має вигляд:

(7.5)

Величина для неї розраховується по виразу .

Покажемо застосування формули (7.5) для значення (екстраполяція):

Друга інтерполяційна формула Ньютона

7.5. Обернена інтерполяція

Задача оберненої інтерполяції полягає в тому, щоб по заданому значенню функції у визначити відповідне їй значення аргументу х.

Припустимо, що функція монотонна і значення у знаходиться між та . Замінимо функцію у першою інтерполяційною функцією Ньютона:

(7.6)

Побудуємо ітераційний процес знаходження значення в відповідності з інтерполяційним методом уточнення кореня нелінійного рівняння (рисунок 25):

звідси:

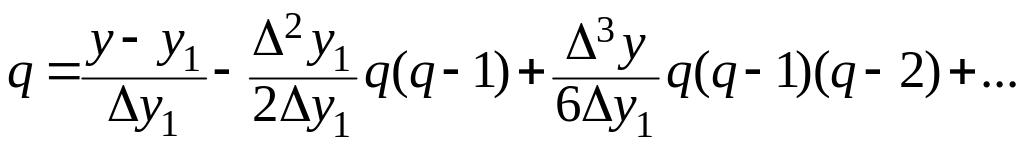
Початкове значення знайдемо із скороченого значення виразу :

.

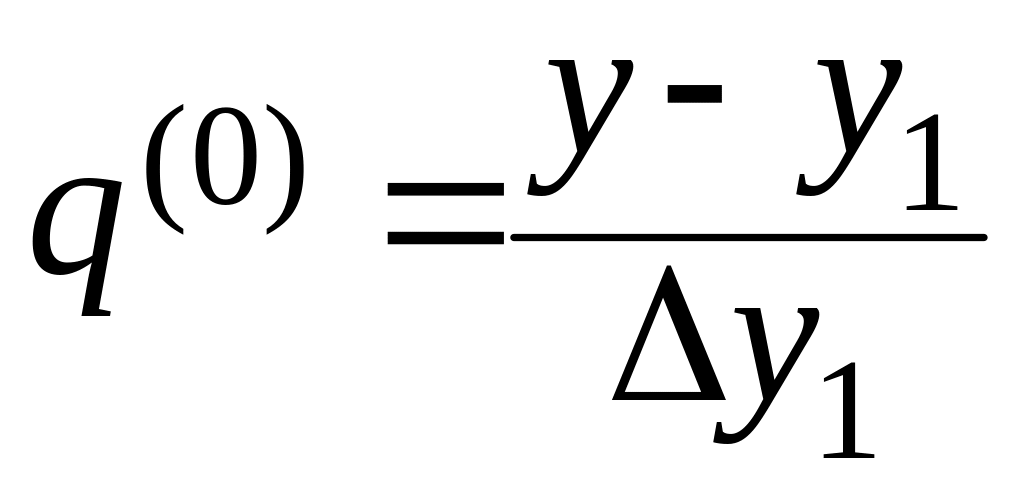Далі створюємо ітераційний процес: ; і т.д. допоки не установляться цифри величини в відповідності з заданою точністю.

Значення шуканого аргументу знаходять з формули: . Тобто .

Приклад. Для даних попередньої задачі знайти х при якому .

Обернена інтерполяція

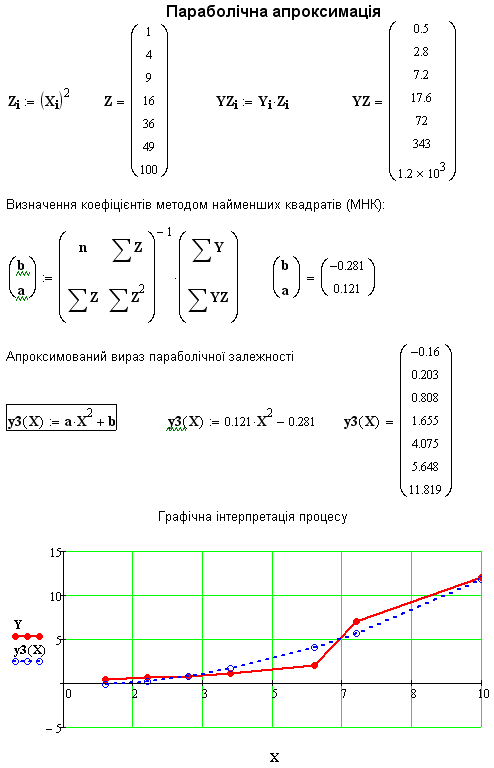
7.6. Апроксимація функцій методом найменших квадратів

При інтерполяції функції, заданої таблицею , знаходилися поліноми, які збігалися із значеннями функції у вузлах інтерполяції.

В режимі апроксимації знаходять відому залежність (пряму, параболу, експоненту, синусоїду тощо) такого вигляду, щоб її графік найближче проходив до усіх значень табличної функції. Така апроксимуюча функція не буде давати точних значень в вузлах інтерполяції, але буде досить близькою до них. Найзручнішою формою близькості є така, за якою сума квадратів різниць між табличною функцією та апроксимуючою функцією в точках таблиці:

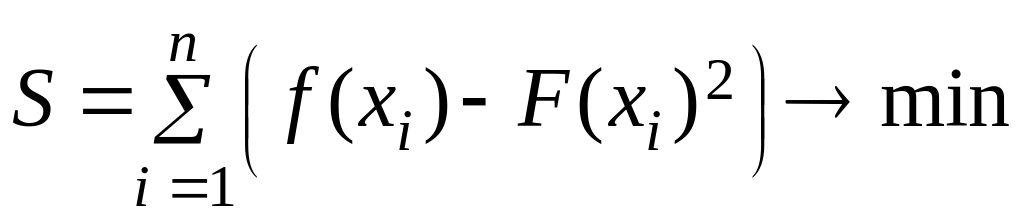(7.7)

Наближення функції у формулі (7.7) називають квадратичним, а сам процес мінімізації – методом найменших квадратів.

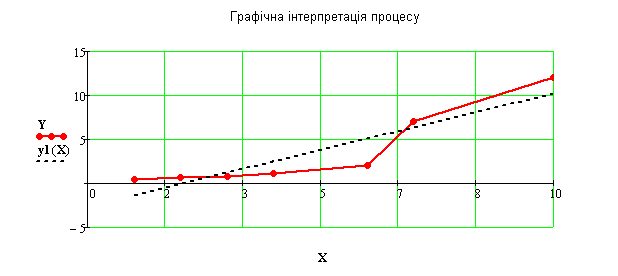
Застосуємо цей метод для найпростішої апроксимації функції прямою лінією (рисунок 29).

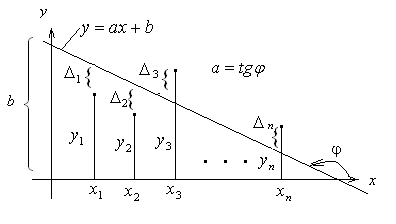
Рисунок 29 – Геометричне представлення лінійної апроксимації

; ;

.

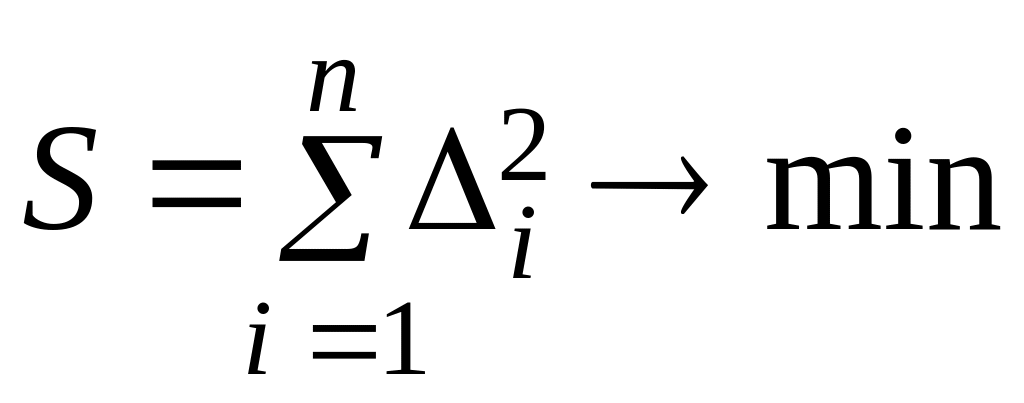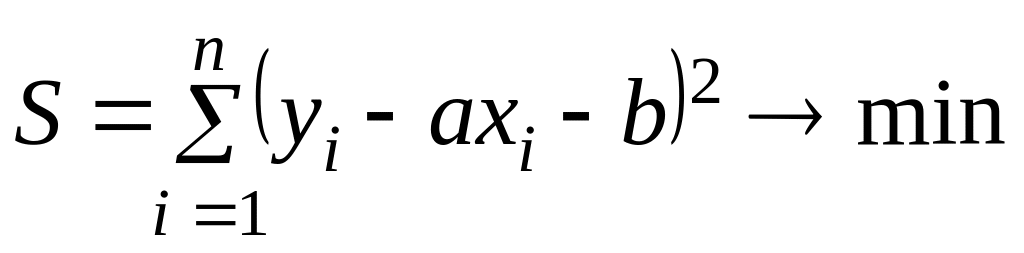Невідомі коефіцієнти прямої a та b знайдемо, якщо прирівняємо до нуля частинні похідні від по невідомим а і b: .

Розпишемо ці похідні:

Скоротивши на та розкривши знак будемо мати:

.

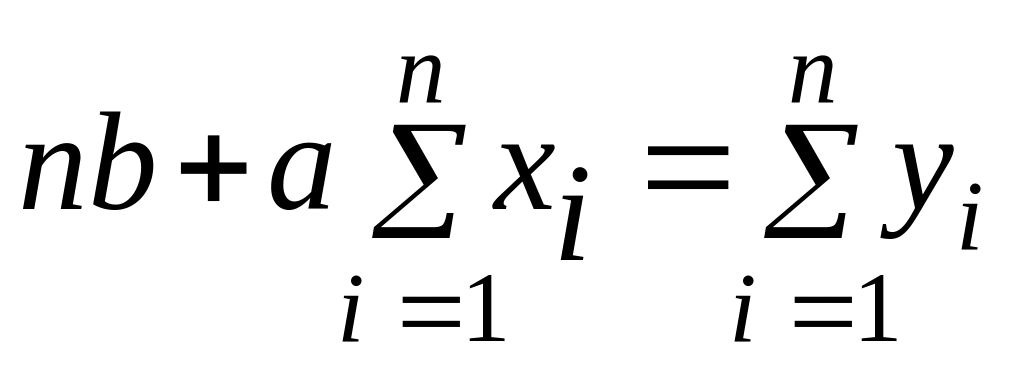
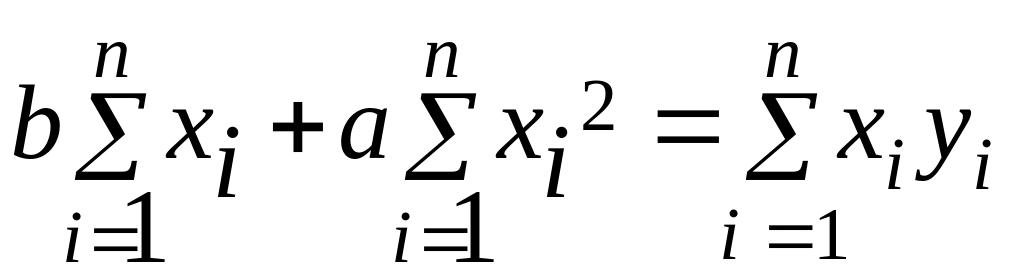Або в матричній формі:

(7.8)

Приклад лінійної апроксимації табличної функції.

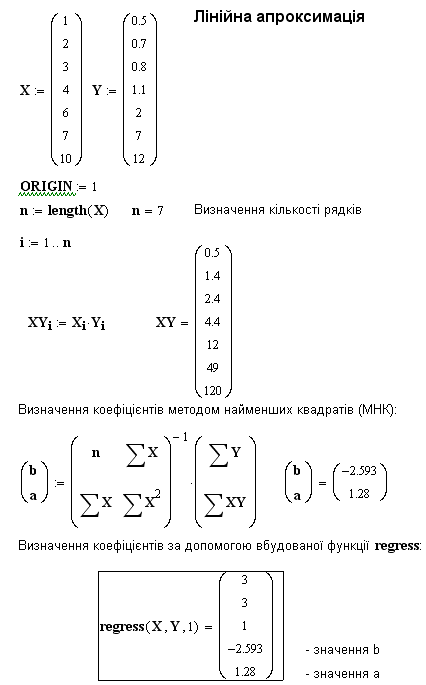
Інструментами системи MathCad можна одержати коефіцієнти прямої та або .

Для апроксимації табличної функції параболою

коефіцієнтами a, b, c квадратичної функції одержуємо із трьох рівнянь

Одержуємо матричне рівняння .

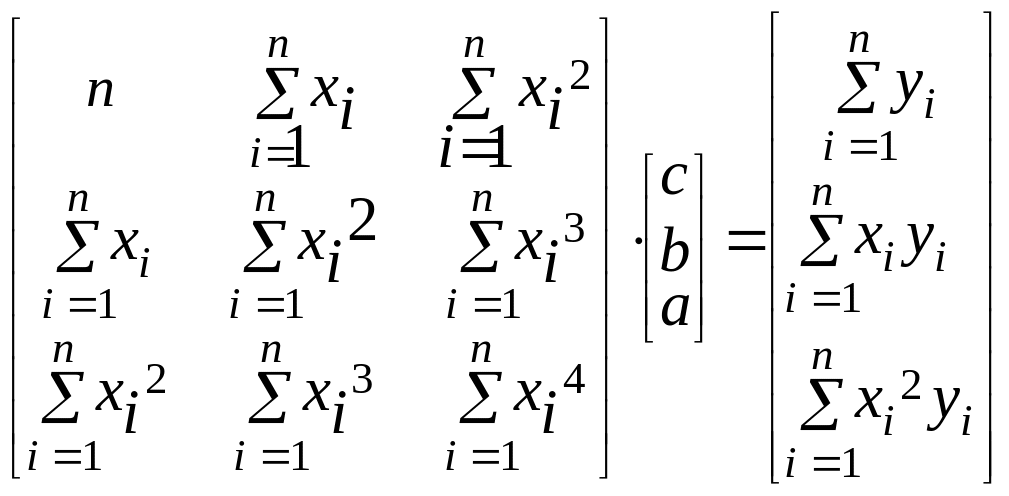Застосуємо розв’язок цього рівняння для попередньої задачі.

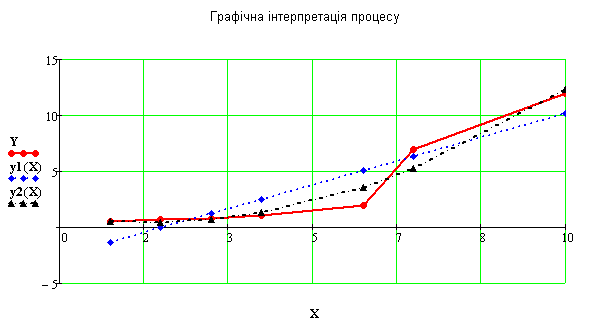
Коефіцієнти a, b, c на MathCad можна одержати: .

Бачимо, що парабола значно краще апроксимує табличні значення .

7.7. Нелінійна апроксимація

Для тих табличних залежностей, де лінійна чи квадратична апроксимація не досить вдалі, можна апроксимувати їх нелінійними залежностями. Для цього їх потрібно лінеаризувати та представити формулою (7.9). Наприклад, якщо припустити, що між величинами х та у існує залежність близька до експоненціальної , то потрібно застосувати лінійну залежність між величинами та х .

Можливі такі види залежностей їх лінеаризації:

1. 

2. 

3. 

4. 

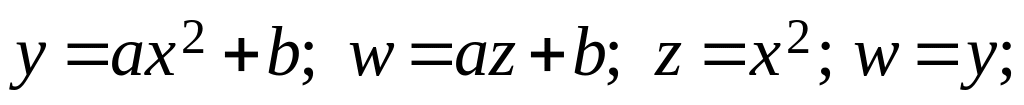
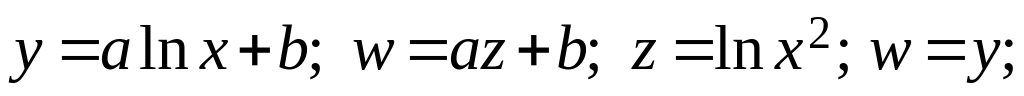
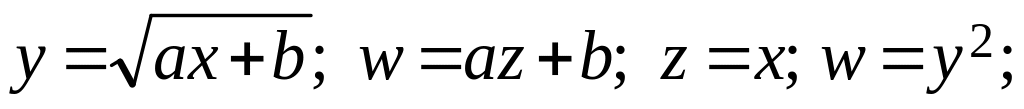
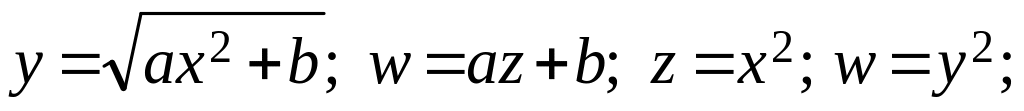5. (7.9)

6. 

7. 

8. 

9. 

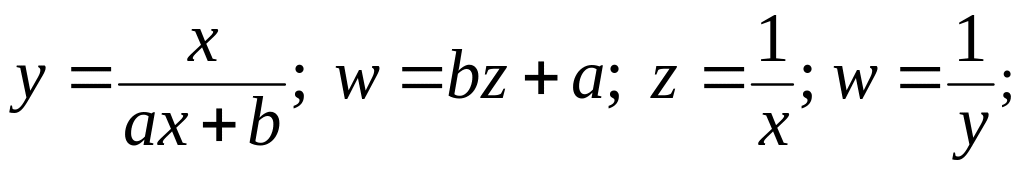
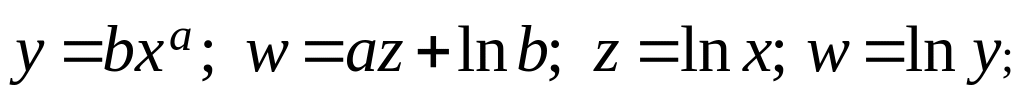
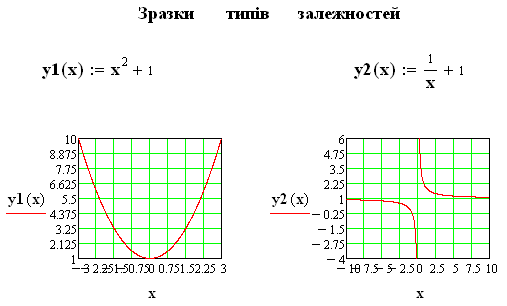
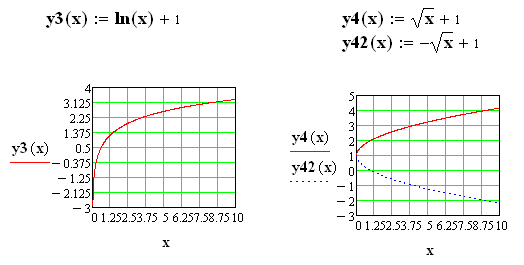
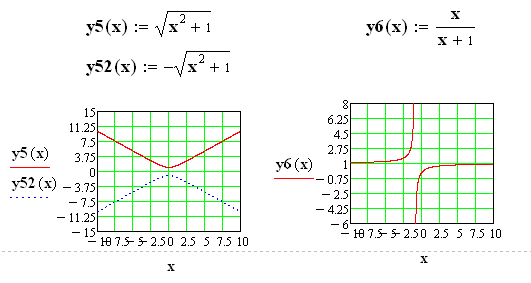
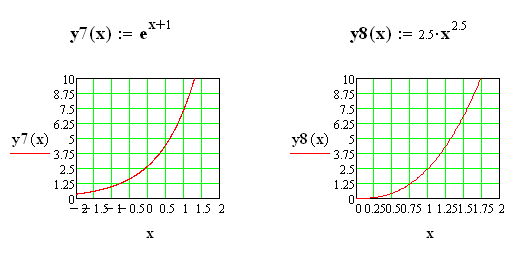
Наведемо приклад параболічної та експоненціальної апроксимації:

та