Как вычислить определенный интеграл по формуле Симпсона?
Если вы искали на данной страничке только метод Симпсона, то настоятельно рекомендую сначала прочитать начало урока и просмотреть хотя бы первый пример. По той причине, что многие идеи и технические приемы будут схожими с методом трапеций.
И
снова, начнём с общей формулы
Рассмотрим
определенный интеграл
,
где
–
функция, непрерывная на отрезке
.
Проведём разбиение
отрезка
на чётное количество равных отрезков.
Чётное количество отрезков обозначают
через 
.
На
практике отрезков может
быть:
два: 
четыре: 
восемь: 
десять: 
двадцать: 
Другие
варианты не припоминаю.
Внимание! Число 
понимается
как ЕДИНОЕ ЧИСЛО. То есть, НЕЛЬЗЯ сокращать,
например,
на
два, получая
.
Запись
лишь обозначает,
что количество отрезков чётно.
И ни о каких сокращениях речи не идёт
Итак,
наше разбиение имеет следующий вид:
Термины
аналогичны терминам метода
трапеций:
Точки 
называют узлами.
Формула
Симпсона для
приближенного вычисления определенного
интеграла имеет следующий вид:
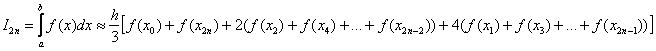где:
–
длина каждого из маленьких отрезков
или шаг;
–
значения подынтегральной функции в
точках
.
Детализируя
это нагромождение, разберу формулу
подробнее:
–
сумма первого и последнего значения
подынтегральной функции;
–
сумма членов с чётными индексами
умножается на 2;
–
сумма членов с нечётными индексами
умножается на 4.
Пример 4
Вычислить
приближенно определенный интеграл по
формуле Симпсона с точностью до 0,001.
Разбиение начать с двух отрезков
Интеграл, кстати, опять неберущийся.
Решение: Сразу обращаю внимание на тип задания – необходимо вычислить определенный интеграл с определенной точностью. Что это значит, я уже комментировалось в начале статьи, а также на конкретных примерах предыдущего параграфа. Как и для метода трапеций, существует формула, которая сразу позволит определить нужное количество отрезков (значение «эн») чтобы гарантированно достичь требуемой точности. Правда, придётся находить четвертую производную и решать экстремальную задачу. Кто понял, о чём я, и оценил объем работы, тот улыбнулся. Однако здесь не до смеха, находить четвертую производную от такой подынтегральной функции будет уже не мегаботан, а клинический психопат. Поэтому на практике практически всегда используется упрощенный метод оценки погрешности.
Начинаем
решать. Если у нас два отрезка разбиения
,
то узлов будет на
один больше: 
.
И формула Симпсона принимает весьма
компактный вид:
Вычислим
шаг разбиения: 
Заполним расчетную таблицу:
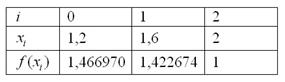Еще
раз комментирую, как заполняется таблица:
В верхнюю строку записываем «счётчик» индексов
Во
второй строке сначала пишем нижний
предел интегрирования 
,
а затем последовательно приплюсовываем
шаг 
.
В
третью строку заносим значения
подынтегральной функции. Например,
если 
,
то 
. Сколько
оставлять знаков после запятой?Действительно,
в условии опять об этом ничего не сказано.
Принцип тот же, что и в методе трапеций,
смотрим на требуемую точность: 0,001. И
прибавляем дополнительно 2-3 разряда.
То есть, округлять нужно до 5-6 знаков
после запятой.
В
результате:
Первичный
результат получен. Теперь удваиваем количество
отрезков до четырёх:
.
Формула Симпсона для данного разбиения
принимает следующий вид:
Вычислим
шаг разбиения: 
Заполним
расчетную таблицу:
Таким
образом:
Оцениваем
погрешность:
Погрешность
больше требуемой точности: 
,
поэтому необходимо еще раз удвоить
количество отрезков:
.
Формула
Симпсона растёт, как на дрожжах:
Вычислим
шаг: 
И снова
заполним расчетную таблицу:
Таким
образом:
Заметьте,
что здесь вычисления желательно уже
расписать более подробно, поскольку
формула Симпсона достаточно громоздка,
и если сразу бУхнуть:
,
то выглядеть сиё бухло будет как халтура.
А при более детальной записи у преподавателя
сложится благостное впечатление, что
вы добросовестно стирали клавиши
микрокалькулятора в течение доброго
часа. Детальные вычисления для «тяжелых»
случаев присутствуют в моём калькуляторе.
Оцениваем
погрешность:
Погрешность
меньше требуемой точности: 
.
Осталось взять наиболее точное
приближение 
,
округлить его до трёх знаков после
запятой и записать:
Ответ: 
с
точностью до 0,001
Пример 5
Вычислить
приближенно определенный интеграл по
формуле Симпсона с точностью до 0,0001.
Разбиение начать с двух отрезков
Это пример для самостоятельного решения. Примерный образец чистового «короткого» оформления решения и ответ в конце урока.
В заключительной части урока рассмотрим еще пару распространенных примеров
Пример 6
Вычислить
приближенное значение определенного
интеграла 
с
помощью формулы Симпсона, разбив отрезок
интегрирования на 10 частей. Точность
вычислений 0,001.
Этот интеграл берётся, правда, новичку взломать его не так-то просто, соответствующий метод решения рассмотрен в примере 5 урока Сложные интегралы. В задачах на приближенное вычисление интеграл не обязан быть непременно неберущимся! Любознательные студенты могут вычислить его точно и оценить погрешность относительно приближенного значения.
Решение: Обратите внимание на формулировку задания: «Точность вычислений 0,001». Смысловой нюанс данной формулировки предполагает, что результаты нужно только округлить до третьего знака после запятой, а не достигнуть такой точности. Таким образом, когда вам предлагается для решения задача на метод трапеций, метод Симпсона, всегдавнимательно вникайте в условие! Спешка, как известно, нужна при охоте на блох.
Используем
формулу Симпсона:
При
десяти отрезках разбиения 
шаг
составляет 
Заполним
расчетную таблицу:
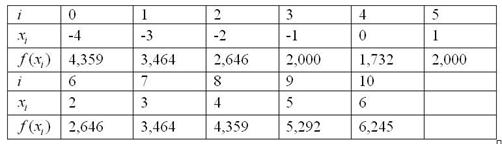
Таблицу рациональнее сделать двухэтажной, чтобы не пришлось «мельчить» и всё разборчиво вместилось на тетрадный лист.
Вычисления,
не ленимся, расписываем подробнее:
Ответ: 
И еще
раз подчеркну, что о точности здесь речи
не идет. На самом деле, ответ может быть
не 
,
а, условно говоря, 
.
В этой связи в ответе не нужно машинально
приписывать «дежурную» концовку: «с
точностью до 0,001»
Пример 7
Вычислить приближенное значение определенного интеграла
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления проводить с точностью до третьего десятичного знака.
Примерная версия чистового оформления и ответ в конце урока, который подошел к концу.
Для приближенного вычисления определенного интеграл применяются и другие методы. В частности, теория степенных рядов со стандартной задачей Приближенное вычисление определенного интеграла путём разложения подынтегральной функции в ряд. Но это уже материал второго курса.
А сейчас настала пора раскрыть страшную тайну интегрального исчисления. Я создал уже больше десятка уроков по интегралам, и это, так скажем, теория и классика темы. На практике же, в частности, при инженерных расчетах – приблизить объекты реального мира стандартными математическими функциями практически невозможно. Невозможно идеально точно рассчитать, площадь, объем, плотность, к примеру, асфальтового покрытия. Погрешность, пусть с десятого, пусть с сотого знака после запятой – но она всё равно будет. Именно поэтому по приближенным методам вычисления написаны сотни увесистых кирпичей и создано серьёзное программное обеспечение для приближенных вычислений. Классическая же теория интегрального исчисления в действительности применяется заметно реже. Но, кстати, без неё – тоже никуда!
Решения и ответы:
Пример
2: Решение: Разбиваем
отрезок интегрирования на 4 части:
Тогда
формула трапеций принимает следующий
вид:
Вычислим
шаг: 
Заполним
расчетную таблицу:
Таким
образом:
Удвоим
количество отрезков: 
Вычислим
шаг: 
Заполним
расчетную таблицу:
Таким
образом:
Оценим
погрешность вычислений:
,
таким образом, требуемая точность
достигнута.
Ответ: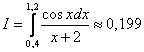 
с
точностью до 0,001
Пример
5: Решение: 1)
Рассмотрим два отрезка разбиения
Вычислим
шаг: 
Заполним
расчетную таблицу:
Таким
образом:
2)
Рассмотрим четыре отрезка разбиения
Вычислим
шаг: 
Заполним
расчетную таблицу:
Таким
образом:
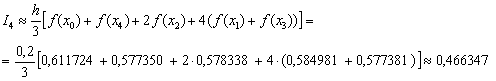Оценим
погрешность:
2)
Рассмотрим восемь отрезков
разбиения
Вычислим
шаг: 
Заполним
расчетную таблицу:
Таким
образом:
Оценим
погрешность:
Ответ: 
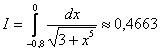с
точностью до 0,0001
Пример
6: Решение: Используем
формулу Симпсона:
,
где: 
, 
, 
В
данном случае: 
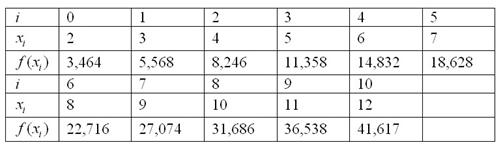Таким
образом:
Ответ: 
Замечательные пределы
На практике у студентов-заочников практически всегда возникает необходимость использовать первый и второй замечательные пределы, о которых и идет речь в данной справке. Также рассмотрены еще три замечательных предела, которые встречаются значительно реже. Все замечательные пределы снабжены дополнительными важными комментариями.
Таблица производных
В справке приведены правила дифференцирования и таблица производных от основных элементарных функций. Таблица снабжена очень важными примечаниями.
Таблица интегралов
В общем-то, почти то же самое, что и в предыдущем пункте. Правила интегрирования и таблица интегралов с моими комментариями.
секунды!