Метод подведения под знак дифференциала для простейших дробей
Переходим
к рассмотрению следующего типа
дробей.
, 
, 
, 
(коэффициенты 
и 
не
равны нулю).
На самом деле пара случаев с арксинусом и арктангенсом уже проскальзывала на урокеМетод замены переменной в неопределенном интеграле. Решаются такие примеры способом подведения функции под знак дифференциала и дальнейшим интегрированием с помощью таблицы. Вот еще типовые примеры с длинным и высоким логарифмом:
Пример 5
Пример 6
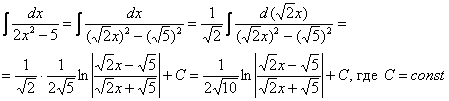
Тут
целесообразно взять в руки таблицу
интегралов и проследить, по каким
формулам и какосуществляется
превращение. Обратите внимание, как
и зачем выделяются
квадраты в данных примерах. В частности,
в примере 6 сначала необходимо
представить знаменатель 
в
виде 
,
потом подвести 
под
знак дифференциала. А сделать это всё
нужно для того, чтобы воспользоваться
стандартной табличной формулой 
.
Да что смотреть, попробуйте самостоятельно решить примеры №№7,8, тем более, они достаточно короткие:
Пример 7
Найти
неопределенный интеграл:
Пример 8
Найти
неопределенный интеграл:
Если Вам удастся выполнить еще и проверку данных примеров, то большой респект – Ваши навыки дифференцирования на высоте.
Метод выделения полного квадрата
Интегралы
вида 
, 
(коэффициенты
и 
не
равны нулю) решаются методом выделения
полного квадрата. На самом деле такие
интегралы сводятся к одному из четырех
табличных интегралов, которые мы только
что рассмотрели. А достигается это с
помощью знакомых формул сокращенного
умножения:
или 
Формулы
применяются именно в таком направлении,
то есть, идея метода состоит в том, чтобы
в знаменателе искусственно организовать
выражения 
либо 
,
а затем преобразовать их соответственно
в 
либо 
.
Пример 9
Найти
неопределенный интеграл
Это простейший пример, в котором при слагаемом – единичный коэффициент (а не какое-нибудь число или минус).
Смотрим
на знаменатель, здесь всё дело явно
сведется к случаю
.
Начинаем преобразование знаменателя:
Очевидно,
что нужно прибавлять 4. И, чтобы выражение
не изменилось – эту же четверку и
вычитать:
Теперь
можно применить формулу
:
После
того, как преобразование
закончено ВСЕГДА желательно
выполнить обратный ход: 
,
всё нормально, ошибок нет.
Чистовое
оформление рассматриваемого примера
должно выглядеть примерно так:
Готово.
Подведением «халявной» сложной функции
под знак дифференциала: 
,
в принципе, можно было пренебречь
Пример 10
Найти
неопределенный интеграл:
Это пример для самостоятельного решения, ответ в конце урока
Пример 11
Найти
неопределенный интеграл:
Что
делать, когда перед
находится
минус? В этом случае, нужно вынести минус
за скобки и расположить слагаемые в
нужном нам порядке: 
. Константу («двойку»
в данном случае) не
трогаем!
Теперь
в скобках прибавляем единичку. Анализируя
выражение, приходим к выводу, что и за
скобкой нужно единичку – прибавить:
Тут
получилась формула
,
применяем:
ВСЕГДА выполняем
на черновике проверку:
,
что и требовалось проверить.
Чистовое
оформление примера выглядит примерно
так:
Усложняем задачу
Пример 12
Найти
неопределенный интеграл:
Здесь при слагаемом уже не единичный коэффициент, а «пятёрка».
(1) Если при находится константа, то её сразу выносим за скобки.
(2) И вообще эту константу всегда лучше вынести за пределы интеграла, чтобы она не мешалась под ногами.
(3)
Очевидно, что всё сведется к формуле
.
Надо разобраться в слагаемом 
,
а именно, получить «двойку»
(4)
Ага, 
.
Значит, к выражению прибавляем 
,
и эту же дробь вычитаем.
(5)
Теперь выделяем полный квадрат. В общем
случае также надо вычислить 
,
но здесь у нас вырисовывается формула
длинного логарифма 
,
и действие
выполнять
не имеет смысла, почему – станет ясно
чуть ниже.
(6)
Собственно, можно применить формулу
,
только вместо «икс» у нас 
,
что не отменяет справедливость табличного
интеграла. Строго говоря, пропущен один
шаг – перед интегрированием
функцию 
следовало
подвести под знак дифференциала: 
,
но, как я уже неоднократно отмечал, этим
часто пренебрегают.
(7) В
ответе под корнем желательно раскрыть
все скобки обратно:
Сложно? Это еще не самое сложное в интегральном исчислении. Хотя, рассматриваемые примеры не столько сложны, сколько требуют хорошей техники вычислений.
Пример 13
Найти
неопределенный интеграл:
Это пример для самостоятельного решения. Ответ в конце урока.
Существуют интегралы с корнями в знаменателе, которые с помощью замены сводятся к интегралам рассмотренного типа, о них можно прочитать в статье Сложные интегралы, но она рассчитана на весьма подготовленных студентов.