Понижение степени подынтегральной функции

Данный приём работает, когда подынтегральные функции нафаршированы синусами и косинусами в чётных степенях. Для понижения степени используют тригонометрические формулы  ,   и  , причем последняя формула чаще используется в обратном направлении:  .

Пример 7

Найти неопределенный интеграл.

Решение:

В принципе, ничего нового здесь нет, за исключением того, что мы применили формулу   (понизив степень подынтегральной функции). Обратите внимание, что я сократил решение. По мере накопления опыта интеграл от   можно находить устно, это экономит время и вполне допустимо при чистовом оформлении заданий. В данном случае целесообразно не расписывать и правило  , сначала устно берем интеграл от 1, затем – от  .

Пример 8

Найти неопределенный интеграл.

Это пример для самостоятельного решения, полное решение и ответ – в конце урока.

Таки обещанное повышение степени:

Пример 9

Найти неопределенный интеграл.

Сначала решение, потом комментарии:

(1) Готовим подынтегральную функцию для применения формулы  .

(2) Собственно применяем формулу.

(3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но, на мой взгляд, так удобнее.

(4) Используем формулу 

(5) В третьем слагаемом снова понижаем степень, но уже с помощью формулы  .

(6) Приводим подобные слагаемые (здесь я почленно разделил   и выполнил сложение  ).

(7) Собственно берём интеграл, правило линейности   и метод подведения функции под знак дифференциала выполняем устно.

(8) Причесываем ответ.

! В неопределенном интеграле нередко ответ можно записать несколькими способами

В только что рассмотренном примере окончательный ответ   можно было записать иначе – раскрыть скобки и даже это сделать еще до интегрирования выражения, то есть вполне допустима следующая концовка примера:

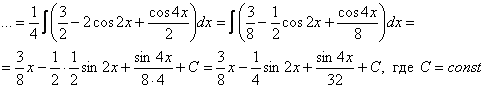
Вполне возможно, что такой вариант даже удобнее, просто я объяснил так, как сам привык решать). Вот еще один характерный пример для самостоятельного решения:

Пример 10

Найти неопределенный интеграл.

Это пример решается двумя способами, и у Вас могут получиться два совершенно разных ответа (точнее говоря, они будут выглядеть совершенно по-разному, а с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.

Подытоживая параграф, сделаем вывод: любой интеграл вида  , где   и   – чётные числа, решается методом понижения степени подынтегральной функции. На практике мне встречались интегралы с 8 и 10 степенями, решать их ужасный геморприходилось, понижая степень несколько раз, в результате чего получались длинные-длинные ответы.

Метод замены переменной

Как уже упоминалось в статье Метод замены переменной в неопределенном интеграле, основной предпосылкой для использования метода замены является тот факт, что в подынтегральном выражении есть некоторая функция   и её производная  :  (функции  ,   не обязательно находятся в произведении)

Пример 11

Найти неопределенный интеграл.

Смотрим в таблицу производных и замечаем формулы  ,  , то есть, в нашем подынтегральном выражении есть функция и её производная. Однако мы видим, что при дифференцировании косинус и синус взаимно превращаются друг в друга, и возникает вопрос: как выполнить замену переменной и что же  обозначать за   – синус или косинус?! Вопрос можно решить методом научного тыка: если мы неправильно выполним замену, то ничего хорошего не получится.

Общий ориентир: в похожих случаях за   нужно обозначить функцию, которая находится в знаменателе.

Прерываем решение и проводим замену

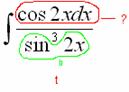В знаменателе у нас всё хорошо, всё зависит только от  , теперь осталось выяснить, во что превратится  . Для этого находим дифференциал  :

Или, если короче:  Из полученного равенства по правилу пропорции выражаем нужное нам выражение:

Итак: 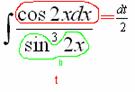Теперь всё подынтегральное выражение у нас зависит только от   и можно продолжать решение

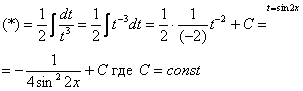
Готово. Напоминаю, что цель замены – упростить подынтегральное выражение, в данном случае всё свелось к интегрированию степенной функции по таблице.

Я не случайно так подробно расписал этот пример, это сделано в целях повторения и закрепления материалов урока Метод замены переменной в неопределенном интеграле.

 А сейчас два примера для самостоятельного решения:

Пример 12

Найти неопределенный интеграл.

Пример 13

Найти неопределенный интеграл.

Полные решения и ответы в конце урока.

Пример 14

Найти неопределенный интеграл.

Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что же обозначать за  , синус или косинус?

Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за   другую функцию, но есть:

Общий ориентир: за   нужно обозначить ту функция, которая, образно говоря, находится в «неудобном положении».

Мы видим, что в данном примере студент косинус «мучается» от степени, а синус – свободно так сидит, сам по себе. 

Поэтому проведем замену:

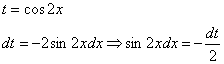
Если у кого остались трудности с алгоритмом замены переменной и нахождением дифференциала  , то следует вернуться к уроку Метод замены переменной в неопределенном интеграле.

Пример 15

Найти неопределенный интеграл.

Анализируем подынтегральную функцию, что нужно обозначить за  ? Вспоминаем наши ориентиры: 1) Функция, скорее всего, находится в знаменателе; 2) Функция находится в «неудобном положении».

Кстати, эти ориентиры справедливы не только для тригонометрических функций.

Под оба критерия (особенно под второй) подходит синус, поэтому напрашивается замена  . В принципе, замену можно уже проводить, но сначала неплохо было бы разобраться, а что делать с  ? Во-первых, «отщипываем» один косинус:

 мы резервируем под наш «будущий» дифференциал 

А   выражаем через синус с помощью основного тригонометрического тождества:

Вот теперь замена: 

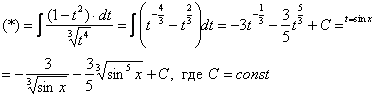
Готово.

Общее правило: Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за   – обозначить другую функцию. Речь идет только об интегралах, где есть косинусы и синусы.

В рассмотренном примере в нечетной степени у нас находился косинус, поэтому мы отщипнули от степени один косинус, а за   обозначили синус.

Пример 16

Найти неопределенный интеграл.

Степени идут на взлёт =). Это пример для самостоятельного решения. Полное решение и ответ в конце урока.