Лабораторная работа № 3 Установление линейной корреляционной связи между двумя случайными величинами (факторами).

Корреляционный и регрессионный анализ

Цель и содержание работы

Цель работы: привить навыки по анализу корреляционной (линейной и нелинейной) связи между двумя случайными величинами и установления линейной регрессионной зависимости между двумя факторами. Установление значимости регрессионной модели.

Содержание работы:

1.Запись исходных данных в виде корреляционной таблицы.

2. Предварительная оценка формы связи между двумя факторами (эмпирической).

3. Выполнение промежуточных расчетов.

4. Вычисление выборочного коэффициента линейной корреляции, установление его значимости и силы тесноты связи.

5. Вычисление коэффициента линейной регрессии. Запись уравнений регрессии.

6. Вычисление коэффициента детерминации регрессионной модели.

7. Содержательная и графическая интерпретация корреляционного и регрессионного анализа.

3.1. Краткие теоретические сведения

Взаимосвязь между случайными величинами изучается с помощью корреляционного анализа в том случае, если взаимодействие величин (факторов) нельзя изолировать от влияния большого числа посторонних факторов.

В основе корреляционного анализа лежит соотношение, существующее между значением одной случайной величины и средним значением другой.

Задача установления корреляционной связи распадается на две:

- первая задача состоит в установлении формы корреляционной связи, т.е. в определении вида функции, связывающей значения одной случайной величины со средним значением другой;

- вторая задача состоит в оценке силы (тесноты) корреляционной связи между факторами.

Если изучаются две случайные величины и , заданные парами значений , причем такие, что связь между ними предположительно можно считать линейной, то первая задача решается путем составления линейных уравнений, называемых уравнениями линейной регрессии:

уравнение линейной регрессии на

уравнение линейной регрессии на

где под и понимаются средние значения случайных величин.

Неизвестные коэффициенты находятся широко используемого метода наименьших квадратов. В общем виде требования метода сводятся , например, для уравнения состоят в минимизации квадратической функции невязки между измерениями и моделью этих измерений

по неизвестным коэффициентам и , при которых проиводные от значения критерия по неизвестным параметрам и равны нулю (необходимое условие существавания экстремума функции):

Решение второй задачи (установление тесноты связи между факторами) сводится к нахождению выборочного коэффициента линейной корреляции

где среднее значение произведений значений случайных величин и

средние значения и ; - средние квадратические отклонения случайных величин и .

Значения изменяются в пределах от –1 до 1, т.е. Чем ближе значение к единице, тем корреляционная связь между переменными и теснее. Значения , близкие к нулю, свидетельствуют о слабой корреляционной связи между факторами.

Если , то анализируемая связь является функциональной, если то корреляционная связь не существует, однако последнее не означает отсутствия других видов связи (например, нелинейной связи).

Направление связи определяется по знаку . Если то связь между случайными величинами прямая, т.е. большему значению одной случайной величины соответствует большее значение другой. Если то связь обратная, т.е. большему значению одной случайной величины соответствует меньшее значение другой. Особо подчеркнем, что выборочный коэффициент линейной корреляции свидетельствует только о тесноте связи и ничего не говорит о факте зависимости одной случайной величины от другой.

Зависимость устанавливается с помощью уравнения регрессии.

Учитывая, что в работе необходимо решать обе задачи, т.е. установить не только форму связи, но и измерить тесноту этой связи, уравнения линейной регрессии целесообразно искать в следующем виде:

- зависимость от .

и -зависимость от ,

где - коэффициент линейной регрессии по

- коэффициент линейной регрессии по ;

В уравнениях линейной регрессии коэффициенты линейной регрессии или характеризуют чувствительность одного фактора при изменении другого фактора на одну единицу.

Так как коэффициенты линейной регрессии выражаются через выборочный коэффициент линейной корреляции с помощью формул:

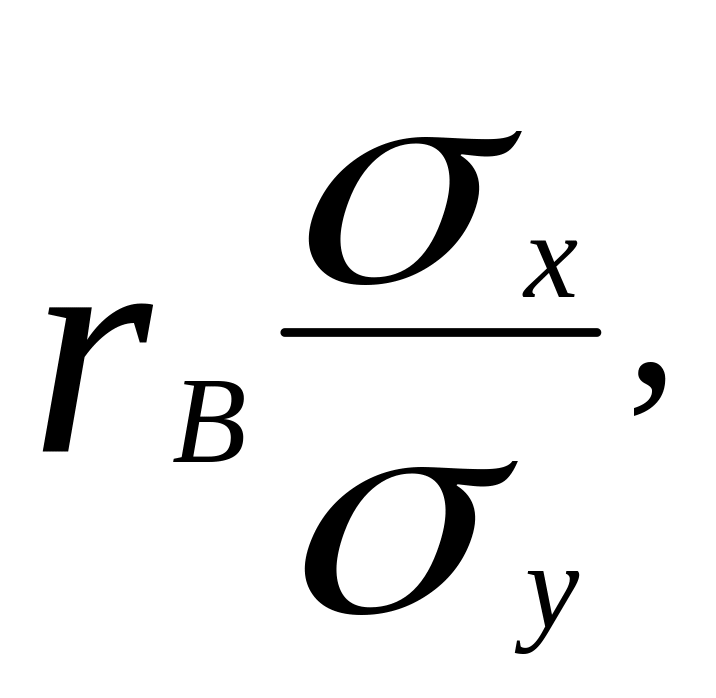
то уравнения линейной регрессии можно записать в виде

и . (*)

Или , (**)

где , , ,

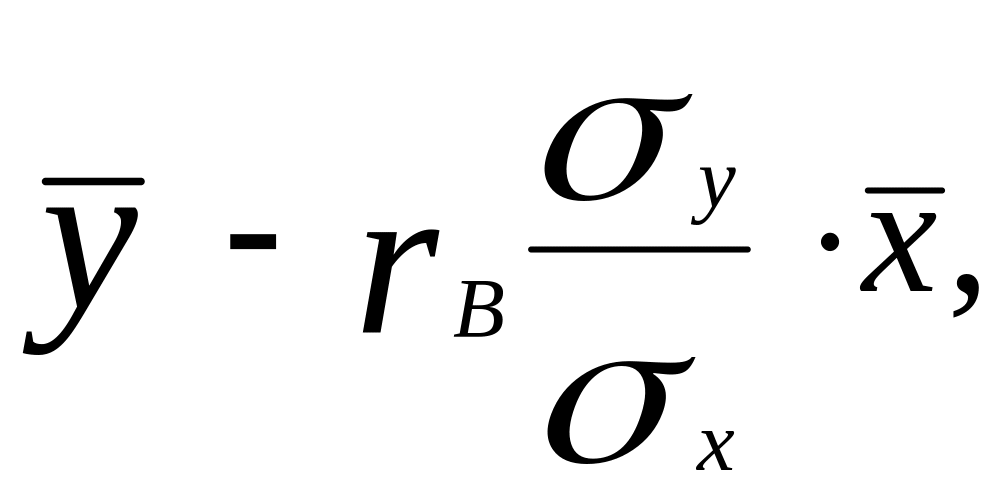Эти выражения получены приведением формулы .

Уравнения называются сопряженными.

При линейной зависимости между и коэффициенты корреляции для каждого из сопряженных уравнений можно записать соответственно как

(Проверить !).

Решение обеих задач корреляционного анализа осуществляется на ограниченном числе наблюдений по выборочным из генеральной совокупности данных, поэтому естественно, что вычисляемые характеристики отличаются от аналогичных характеристик генеральной совокупности.

Если выборочный коэффициент линейной корреляции не равен нулю то еще нельзя заключить, что и коэффициент линейной корреляции генеральной совокупности также не равен нулю . Возможно, значение получилось случайно, поэтому необходимо убедиться в том, что вычисленное значение неслучайно, что она действительно отличается от нуля на значимую величину, и это значение можно перенести на .

Проверка этой гипотезы осуществляется по критерию Стьюдента, путем сравнения наблюдаемого значения случайной величины с критическим значением , взятым из таблиц распределения критических точек Стьюдента (таблица Приложения), где - с.к.о. коэффициента корреляции.

Подобные рассуждения в случае необходимости можно провести и относительно вычисленных по выборочным данным значений коэффициентов линейной регрессии

и .

Оценка существенности (значимости) уравнения регрессии в целом, т.е. проверка адекватности модели производится путем расчета критерия Фишера и сопоставления его с табличным (критическим). критерий представляет собой отношение факторной дисперсии к остаточной дисперсии, каждая из которых рассчитана на одну степень свободы:

,

где число параметров в уравнении регрессии;

число степеней свободы для факторной дисперсии;

число наблюдений;

число степеней свободы для остаточной дисперсии.

Уравнение регрессии значимо, если с вероятностью , где уровень значимости. В этом случае нулевой гипотезой является предположение о том, что уравнение регрессии не зачимо. Следовательно, альтернативная гипотеза уравнение регрессии значимо.

Отметим, что если форма связи между двумя случайными величинами более сложная,

то иногда с помощью специальной замены от нелинейных связей можно перейти к линейным, т.е. провести линеаризацию.

1. Если связь типа гиперболической то замена приводит к линейной связи

2. Если связь типа показательной 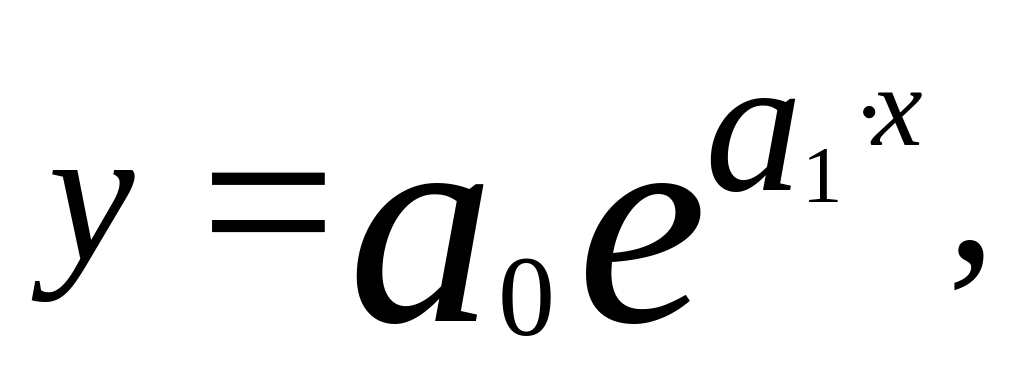то замена

приводит к линейной связи .

3. Если связь типа степенной то замена приводит к линейной связи .

4. Если связь типа логарифмической , то замена приводит к линейной связи

Итак, в корреляционном анализе количественно оценивается связь между двумя (или несколькими) случайными величинами. Его применение позволяет определить наличие и силу связи между переменными.

Измерить тесноту связи между коррелируемыми величинами – значит определить, насколько вариация результативного признака обусловлена вариацией факторного (факторных) признака (признаков).

Существует универсальный показатель - корреляционное отношение (или коэффициент корреляции по Пирсону), применимое ко всем случаям корреляционной зависимости независимо от формы этой связи (линейной или нелинейной).

Различают эмпирическое и теоретическое корреляционное отношения.

Эмпирическое корреляционное отношение рассчитывается по группировке (или корреляционной таблице) как корень квадратный из отношения межгрупповой дисперсии результативного признака к общей дисперсии результативного признака т.е.

или ,

где - общее среднее; - среднее значение группы.

Теоретическое корреляционное отношение определякется на основе выравненных (теоретических) значений результативного признака рассчитанных по уравнению регрессии (для любой формы связи), по формуле

или .

Если обозначить общая дисперсия, факторная дисперсия, то отношение - называется коэффициентом детерминации.

Общая дисперсия эмпирического ряда характеризует вариацию результативного признака за счет всех факторов, включая и фактор , т.е. измеряет общую вариацию величины а дисперсия теоретического ряда, т.е. характеризует вариацию результативного признака за счет вариации только фактора (при прочих равных условиях). Коэффициент детерминации или - показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора на вариацию

В основе исчисления и эмпирического и теоретического корреляционного отношения лежит правило сложения дисперсий, согласно которому

,

где остаточная дисперсия, отражающая влияние на вариацию результативного признака всех остальных факторов (кроме ), не учтенных в модели (в уравнении регрессии). То есть остаточная дисперсия отражает необъясненные расхождения между эмпирическими и теоретическими значениями результативного признака и рассчитывается по формуле

Так как , то

индекс корреляции.

В случае нелинейной регрессии . Если , то это означает, что признак не коррелирован с фактором Случай означает полную зависимость вариации от вариации Обычно при говорят о малой зависимости между коррелируемыми величинами, при - о средней, при - о зависимости выше средней и при - о большой, сильной зависимости.

Корреляционное отношение применимо как для парной, так и для множественной корреляции независимо от формы связи (и линейной и нелинейной). В этом смысле его можно назвать универсальным показателем тесноты связи.

В случае линейной корреляции или , а коэффициент детерминации .

Регрессионный анализ позволяет установить, как в среднем изменяется результативный

признак под влиянием одного или нескольких факторов.

По составленному уравнению линейной регрессии можно находить значение одной случайной величины в зависимости от значения другой, не заданной в таблице, если значение последней соответствует тем же условиям, при которых было составлено уравнение. Это позволяет с помощью уравнений линейной регрессии производить недолгосрочное планирование и прогноз.