Лабораторный практикум по приложениям математической статистики

Целью постановок и выполнения лабораторных работ является привитие студентам навыков и культуры статистического мышления, вычислительных навыков. Привитие мысли и убеждений в том, что в статистических данных обследований массовых жизненно важных явлений содержится очень полезная информация об объекте и ее можно извлечь только в том случае, когда обработка этих массивов данных производится по алгоритмам, смысл которых понятен студенту. Только в этом случае возможна осмысленная интерпретация полученной информации, выходных данных алгоритмов.

Лабораторная работа № 1

Первичная обработка результатов наблюдений Цель и содержание лабораторной работы № 1

Цель работы: привить навыки первичной обработки эмпирических данных с помощью методов математической статистики: получение из выборочных данных эмпирического закона распределения исследуемых признаков, событий, процессов; вычисление числовых характеристик этих распределений; доверительных интервалов параметров распределений, в которых с заданной вероятностью находятся соответствующие числовые характеристики генеральной совокупности; содержательная интерпретация потученных усредненных числовых хпрактеристик распределений признаков.

Содержание работы:

1. Группировка данных в вариационный ряд ( частот 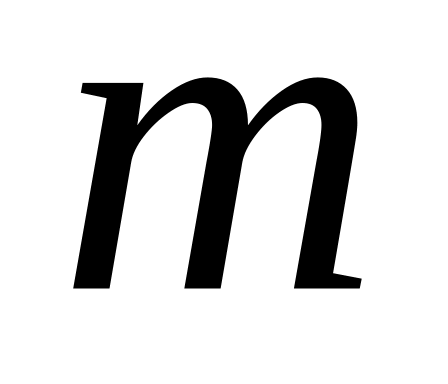, частостей 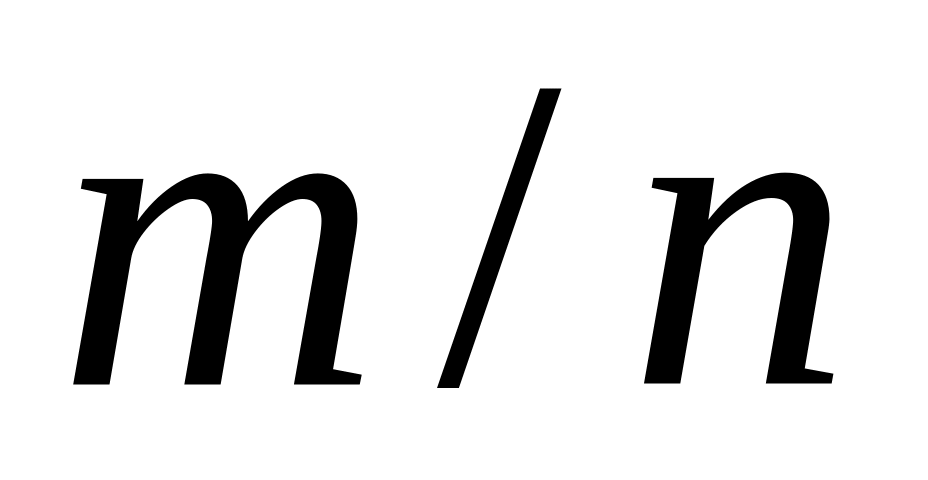и функции распределения. ).

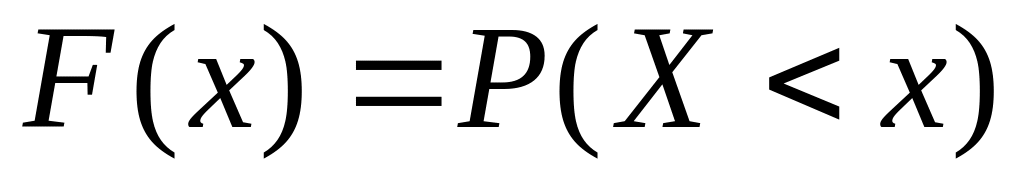2. Графическое изображение вариационного ряда и эмпирической функции распределения.

3. Вычисление основных числовых характеристик выборочной совокупности.

4. Вычисление доверительных интервалов числовых характеристик изучаемой совокупности данных с заданной надежностью (вероятностью).

5. Содержательная интерпретация результатов первичной обработки данных по условию задачи.

6. Формулировка выводов по выполненной работе.

Форма отчета:

1. Представление работы по указанному в методичке образцу.

2. Самостоятельное изучение теоретического материала с помощью предлагаемых контрольных вопросов и краткие письменные ответов на все эти вопросы.

3. Устное собеседование по работе, сдача зачета по письменным ответам на контрольные вопросы.

1. Краткие теоретические сведения и план выполнения работы

Изучение свойств случайных величин методами математической статистики основано на первичной обработке выраженных в числовой форме результатов массовых выборочных наблюдений.

Закономерность, выявленная на основе массового (выборочного) наблюдения, называется статистической зависимостью.

Целью первичной обработки является представление первичной числовой информации в сжатой форме, а также получение сведений об основных закономерностях изучаемой совокупности случайных величин в выборке, соответственно и в генеральной совокупности.

В математической статистике различают генеральную и выборочную совокупности.

Под генеральной совокупностью понимается все мыслимое множество значений случайных признаков, объектов, обладающих общностью некоторого, изучаемого в данном исследовании, признака. Это множество, как правило, счетное. Примеры: гипотетически вызможные значения некоторого изучаемого признака (однотипных предприятий, лидей, предметов и т.п.).

Выборочная совокупность (выборка) – эта часть генеральной совокупности, которая фактически изучается.

Для того чтобы по выборке можно было достаточно уверенно судить о свойствах генеральной совокупности, она должна быть представительной (репрезентативной), т.е. достаточной по численности, случайной по отбору с соблюдением равной возможности каждого элемента генеральной совокупности попасть в выборку.

Теоретической основой выборочного метода является теорема Чебышева. Статистические закономерности обнаруживаются при массовом наблюдении благодаря действию так называемого закона больших чисел. Сущность закона больших чисел заключается в том, что по мере увеличения числа наблюдений влияние случайных факторов (причин), определяющих значение признака у единиц совокупности, взаимопогашаются в общих характеристиках совокупности (например, в средних величинах) и на поверхность выступает действие основных факторов, которые и определяют закономерность.

Таким образом, массовые явления – основа статистики и одна из составляющих ее метода.

Теорема. С вероятностью, сколь угодно близкой к достоверности, можно утверждать, что при достаточно большом числе наблюдений, ограниченной дисперсии генеральной совокупности попарно независимых случайных величин разность между их средним арифметическом и средним арифметическим их математических ожиданий будет сколь угодно малой, т.е.

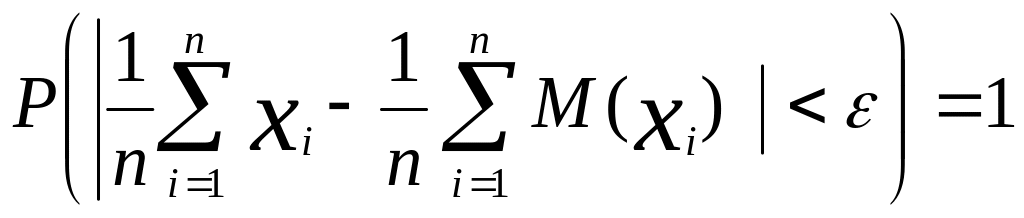
в частности ,

где - средняя для выборочной совокупности;

где - средняя для генеральной совокупности;

сколь угодно малое положительное число.

Итоги эмпирических наблюдений (выборка) представляют собой статистический ряд -таблицу значений изучаемой случайной величины, в которой содержится информация о числовых характеристиках выборки, следовательно и о числовых характеристиках генеральной совокупности. Эти числовые характеристики можно вычислить предварительно сгруппировав полученные первичные данные.

Первичная обработка результатов наблюдений состоит из нескольких этапов, позволяющих в конечном итоге рассчитать обобщающие показатели (характеристики). Рассмотрим содержание каждого из них.

Этап 1. Группировка данных в вариационный ряд и представление его в виде функции распределения.

Для того, чтобы статистические данные представить в виде вариационного ряда с равноотстоящими вариантами (переменными) необходимо:

1. Набрать исходные данные (по варианту) в один столбик на экране Excel и проранжировать их нажатием на панели инструментов кнопку от А до Я.

2. В столбике эмпирических данных найти наименьшее 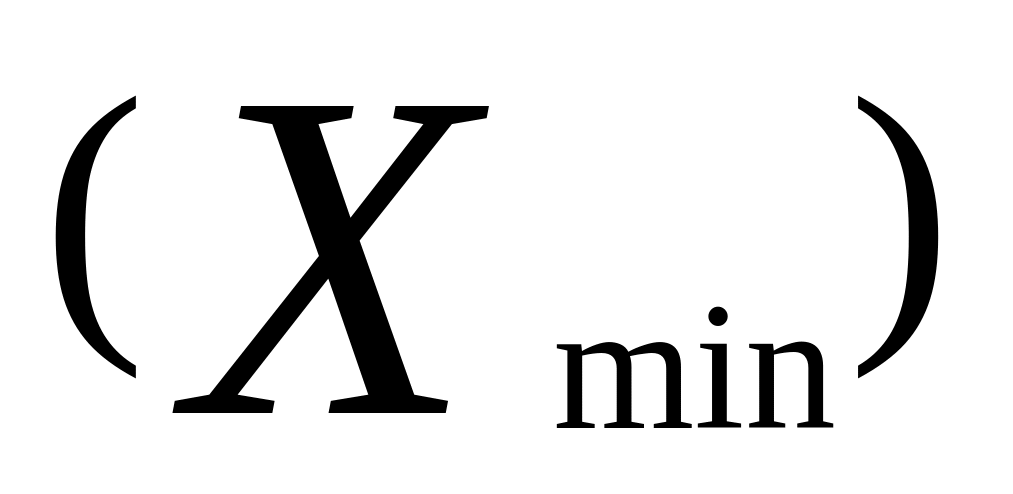и наибольшее 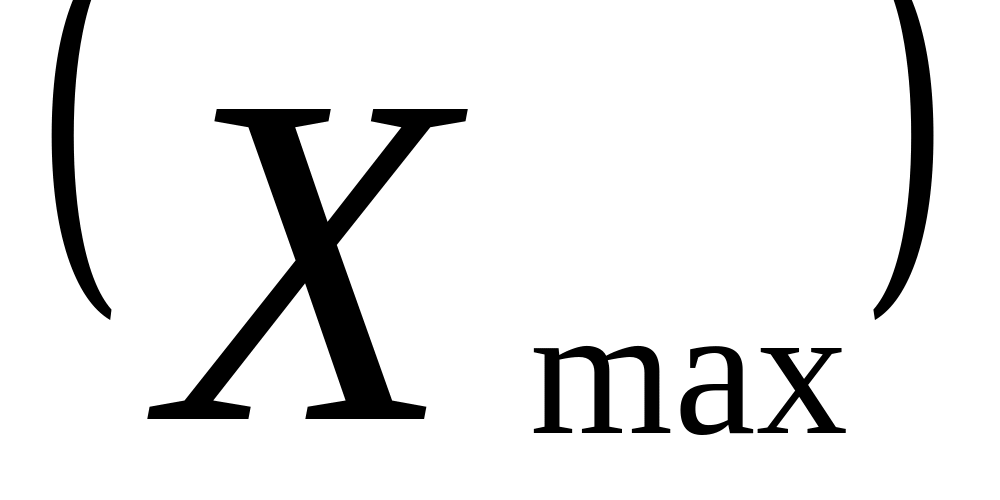значения.

3. Определить размах варьирования .

4. Наметить число интервалов группировки (рекомендуется выделить от 5 до 20 групп так, чтобы каждая группа была достаточно наполнена значениями вариант). Можно также воспользоваться формулами

, , ,

где число групп, объем выборки.

5. Определить длину интервала

.

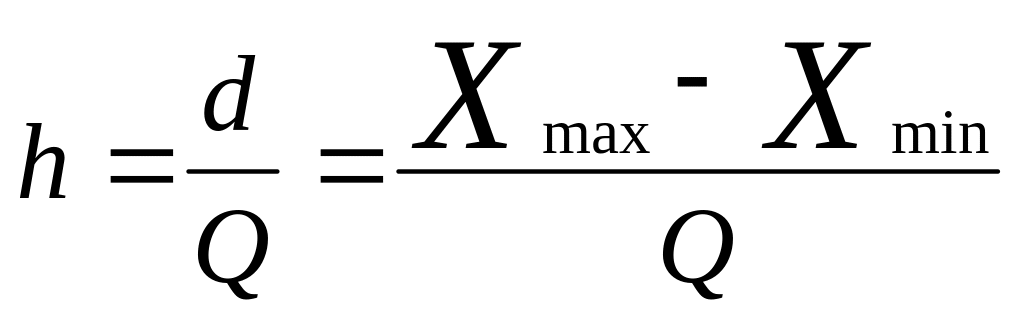Вычисленное отношение следует округлить до удобного значения.

Искодные данные n, - занести на экран Excel.

6. Записать интервалы группировок и расположить их в порядке возрастания границ:

…,

где нижняя граница первого интервала. За берется удобное “круглое” число, не большее , верхняя граница последнего интервала должна быть не меньше . Это делается для того, чтобы интервалы содержали все исходные значения случайной величины.

7. Разнести исходные данные по интервалам группировок, т.е. подсчитать по исходной таблице число значений случайной величины, попадающих в указанные интервалы. Если некоторые значения совпадают с границами интервалов, то их относят либо только к предыдущему, либо к последующему интервалу. Каждое случайное число должно быть отнесено только к одному из интнрвалов (группе)!

Записать интервальный ряд частот и относительных частот

		…….
		…….
		…….

8. От интервального ряда перейти к дискретному. Для этого каждый интервал заменить его средним значением, оставив частоты и относительные частоты (частости) без изменения:

				……
				…….
				…….
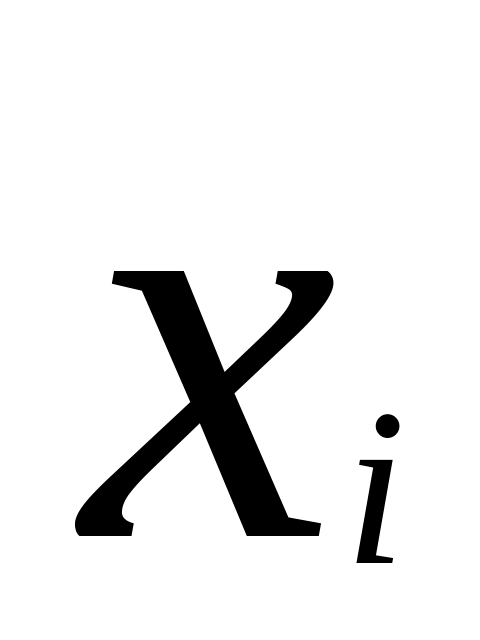
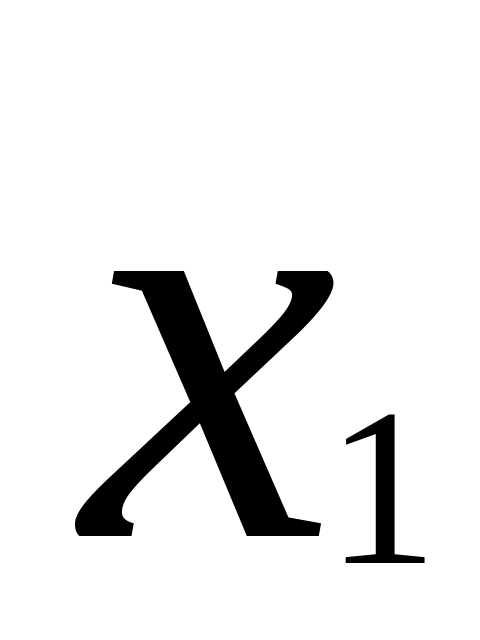
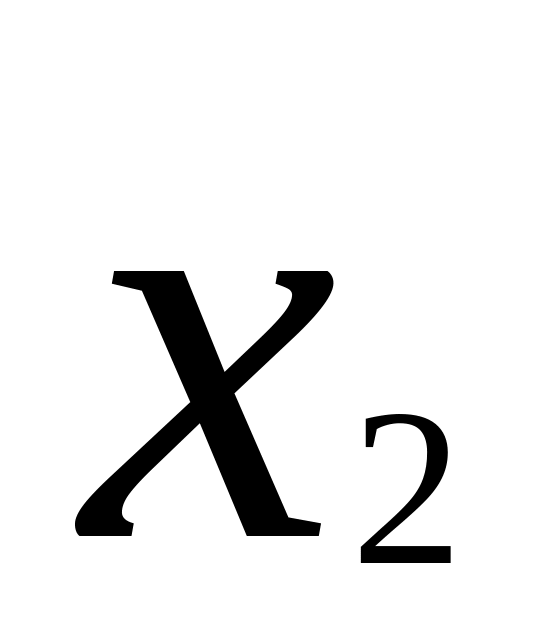
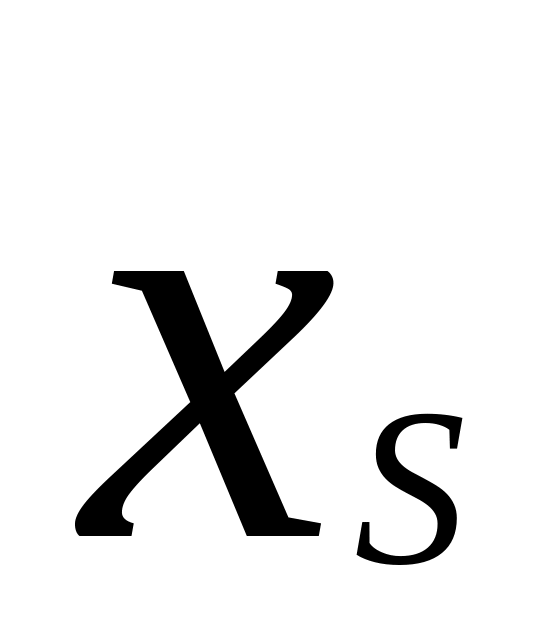
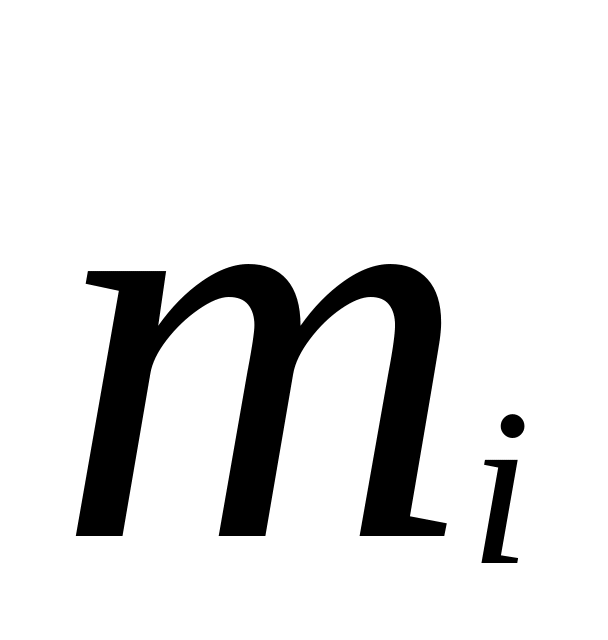
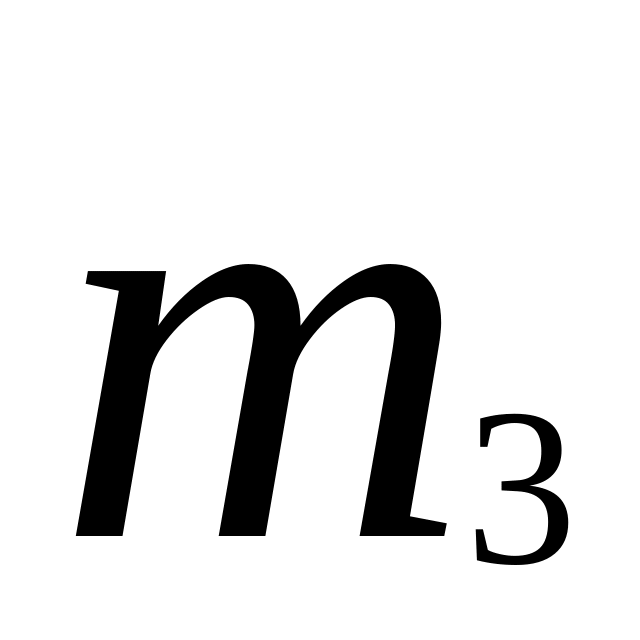
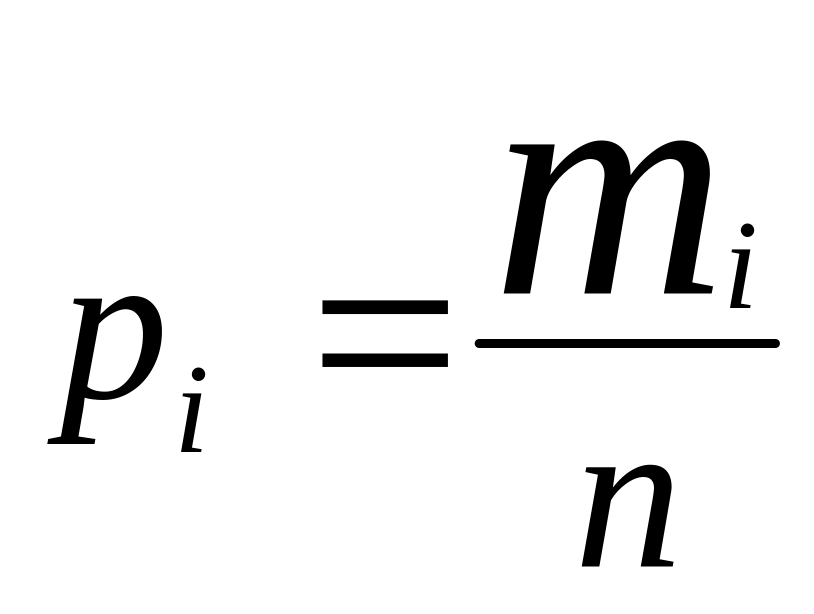
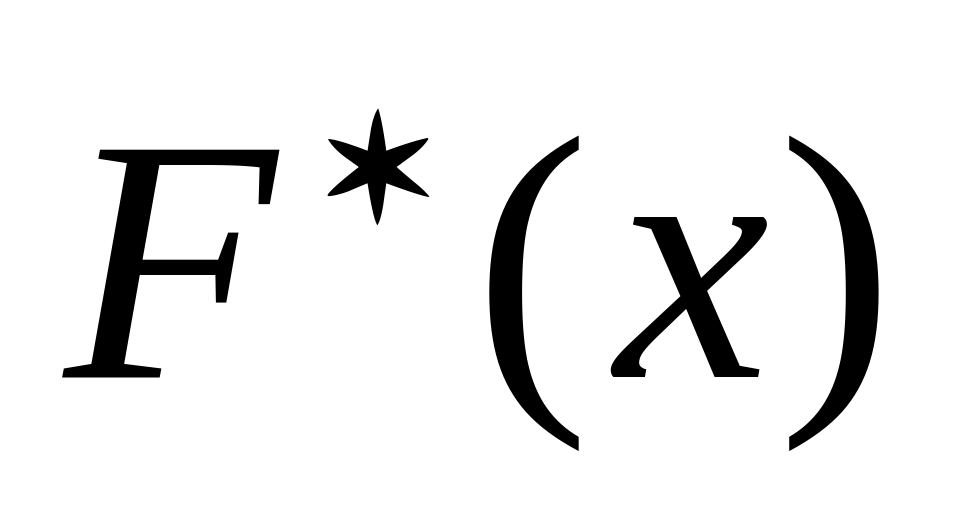
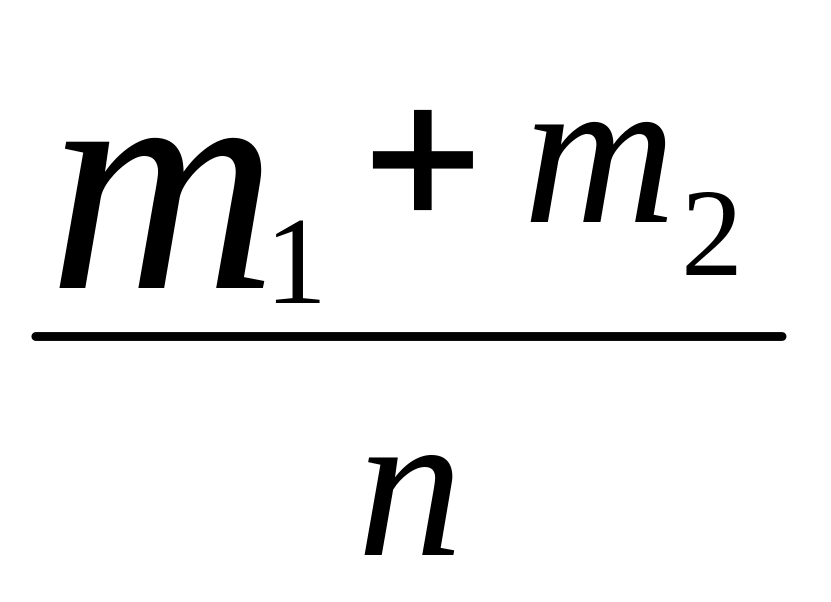
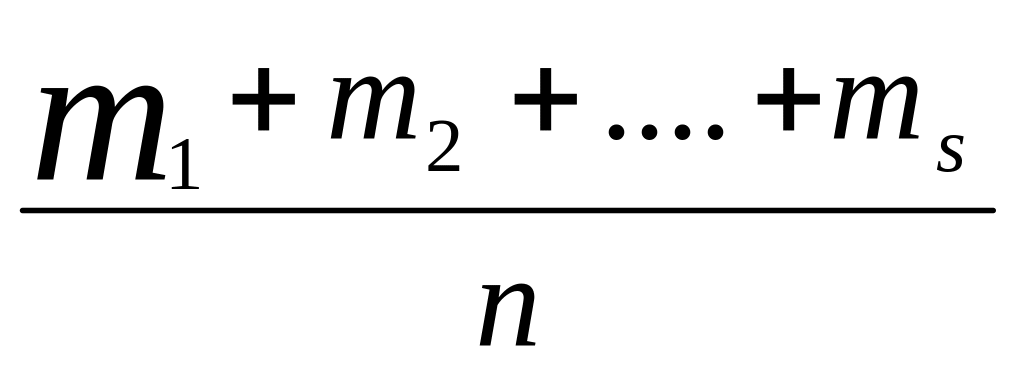
	0			……		1

где .

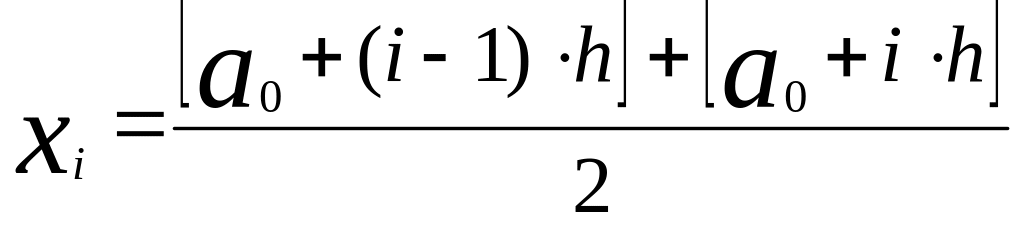8. Записать эмпирическую функцию распределения Здесь для каждого значения суммируются вероятности тех значений которые лежат левее точки

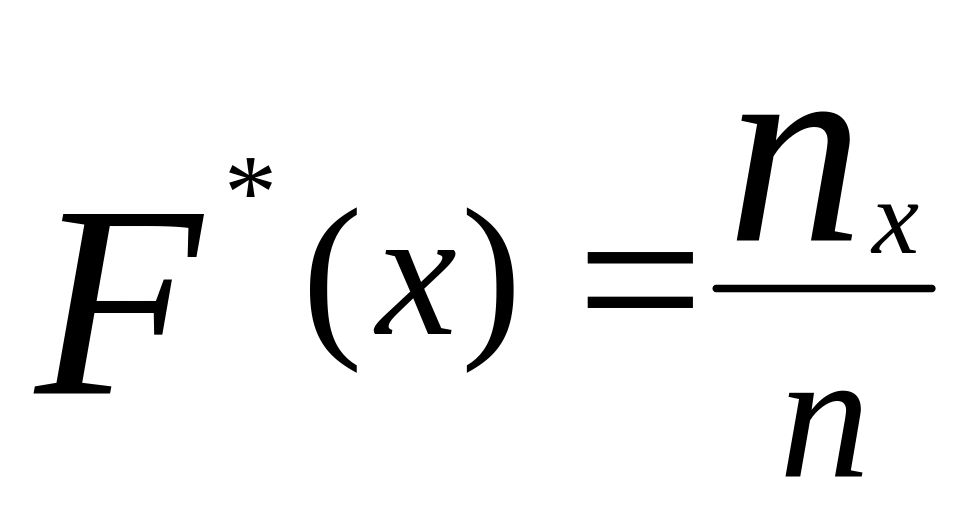, где число вариант (переменных) в последней таблице, значения которых меньше чем ;

объем выборки, т.е.

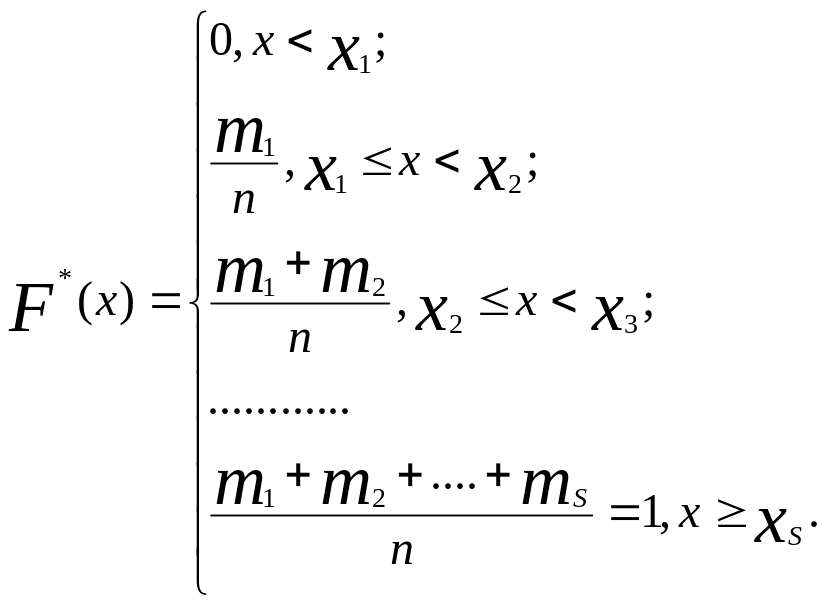
Возрастающая функция определяет относительную частоту события

Замечание 1. Интервалы необязательно брать равными по длине. На участках, где значения располагаются “гуще”, удобнее брать более мелкие интервалы, а там где реже – более крупные.

Замечание 2. Появление “граничных” значений нежелательно, это ведет к смещению эмпирического распределения от его истинного положения на числовой оси либо влево, либо вправо; выбирая границы, регулируя длину интервала, следует этого избегать.

Замечание 3. Если для некоторых получены “нулевые”, либо малые значения частот , то необходимо перегруппировать данные, укрупняя интервалы.

Этап 2. Графическое изображение ряда и эмпирической функции распределения.

Графически интервальный вариационный ряд изображается в виде либо гистограммы частот – ступенчатой столбчатой фигуры, состоящей из прямоугольников, основанием которых служат интервалы группировки , а высоты равны отношению частоты к длине интервала либо в виде гистограммы частот, основанием которых служат интервалы группировки , а высоты равны частотам

Дискретный вариационный ряд графически изображается в виде полигона частот или относительных частот.

Полигон частот – это ломаная линия, отрезки которой соединяют точки с координатами

Полигон относительных частот – это ломаная линия, отрезки которой соединяют точки с координатами

Эмпирическая функция распределения графически изображается в виде линии, изменяющейся скачкообразно (ступенчатая фигура). На оси ОХ откладываются значения вариантов групп, а на оси OY – соответствующие им вероятности, вычисляемые по формуле

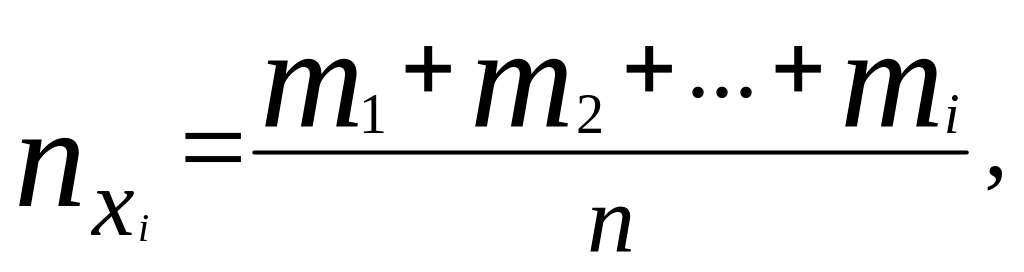
скачки происходят при переходе от одного интервала вида к другому.

Графическое изображение вариационных рядов и эмпирической функции распределения лучше уяснить на конкретном примере в разделе 1.2.

Этап 3. Вычисление числовых характеристик.

Условно числовые характеристики эмпирических распределений разделяются на начальные и центральные. Центральные моменты выражаются (вычисляются) через начальные. Все начальные и центральные моменты являются средними величинами.

Вычисление начальных эмпирических моментов (начальных и центральных средних).

Начальные моменты вычсляются относительно начала координат (нуля) числовой оси, а центральные моменты вычисляются относительно выборочного среднего. Все центральные моменты выражаются через начальные.

Начальные моменты.

1. 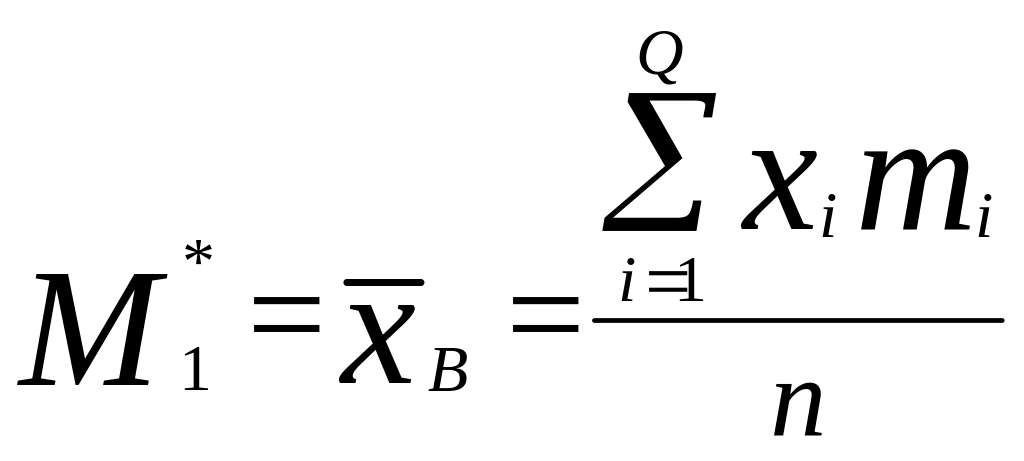- первый начальный момент (оценка математического ожидания выборки). Называется выборочной средней.

2. 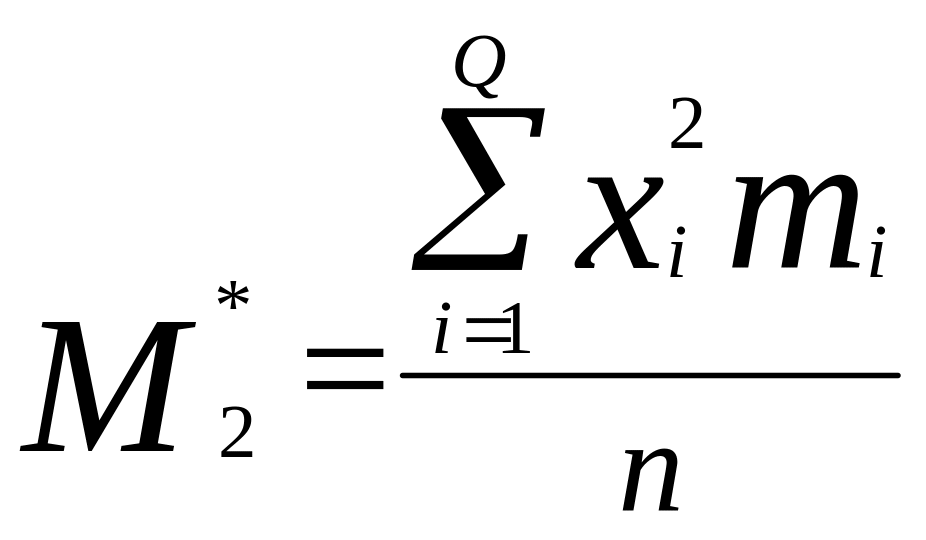- второй начальный момент;

3.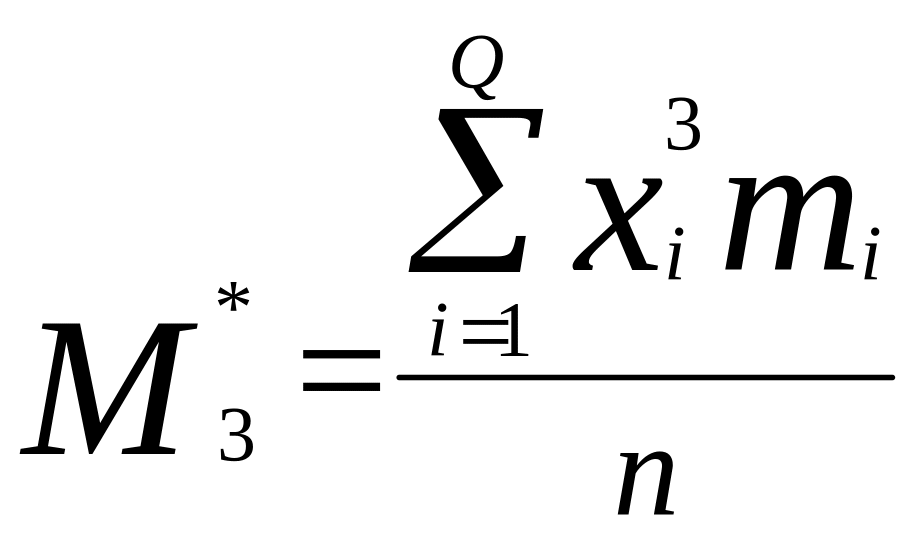 - третий начальный момент;

4. 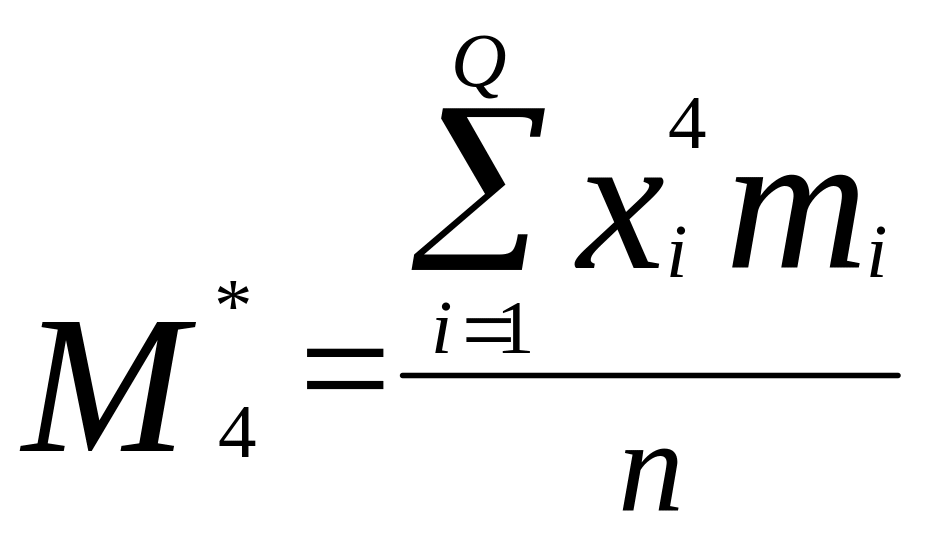- четвертый начальный момент.

Центральные моменты.

5. 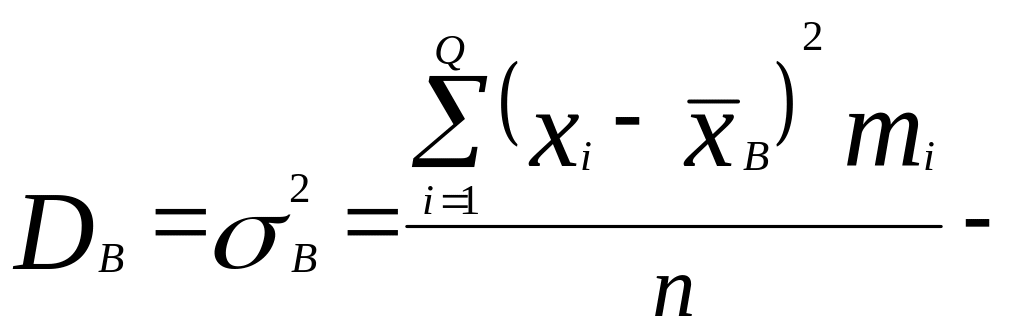дисперсия выборки (по определению)

или - второй центральный момент (все центральные моменты вычисляются относительно оценки математического ожидания ).

7. Среднее квадратическое отклонение (с.к.о.)

Все центральные моменты, вычисленные усреднением, являются смещенными, т.е. содержат систематические ошибки. Эти ошибки необходимо устранить. Устранение (исправление) этих ошибок в разных центральных моментах производится по разным формулам.

8. Исправленная дисперсия

или , если - малая

9. Исправленное среднее квадратическое отклонение

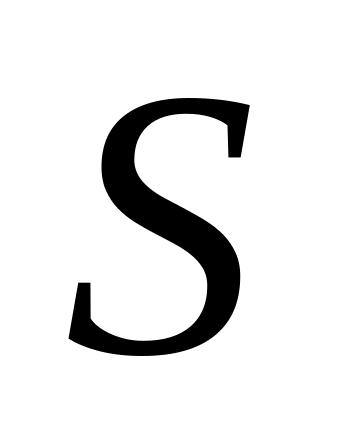
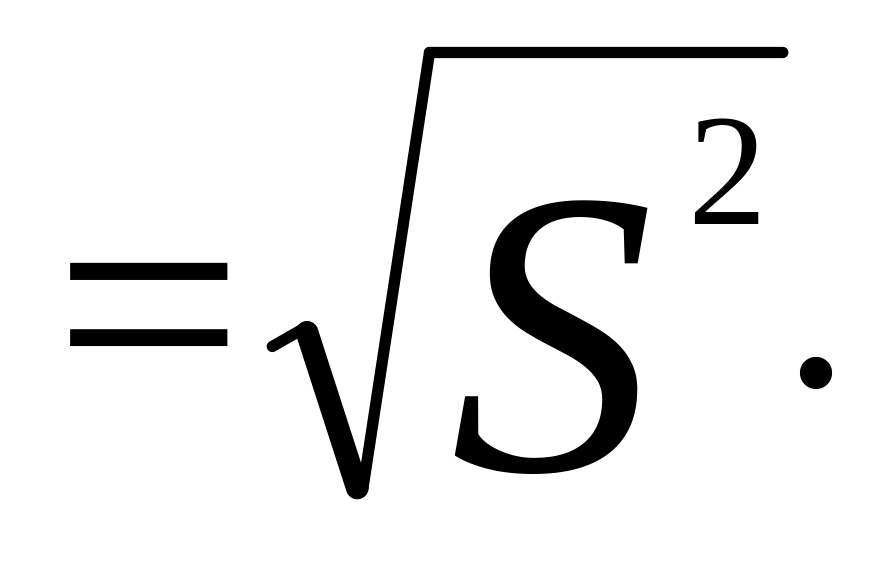
10. Коэффициент асимметрии 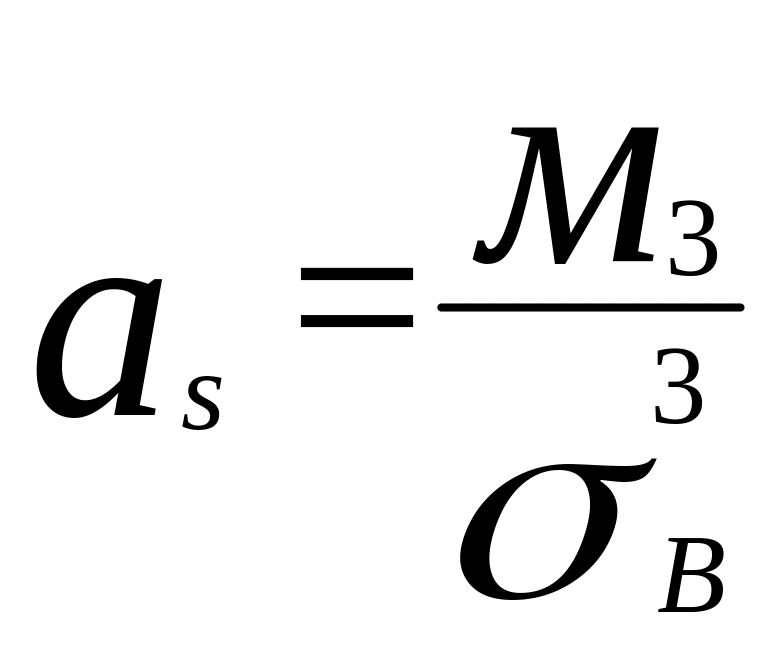, 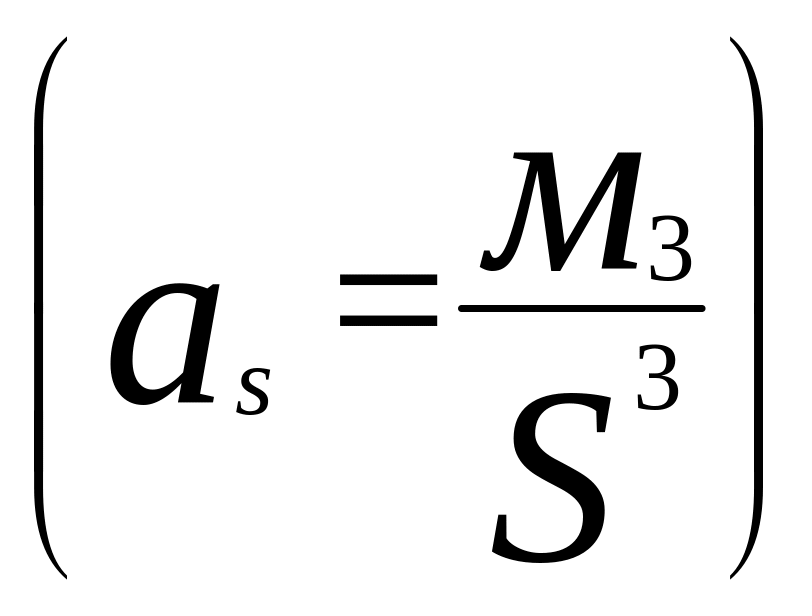-характеризует асимметрию распределения случайных чисел от нормального распределения по горизонтали;

где центральный эмпирический момент третьего порядка, он вычисляется либо формуле

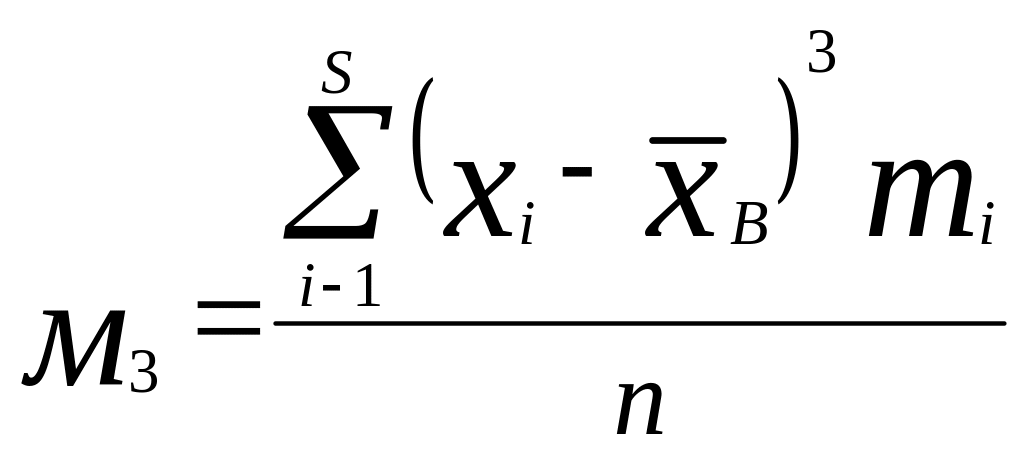либо по формуле .

10. Коэффициент эксцесса 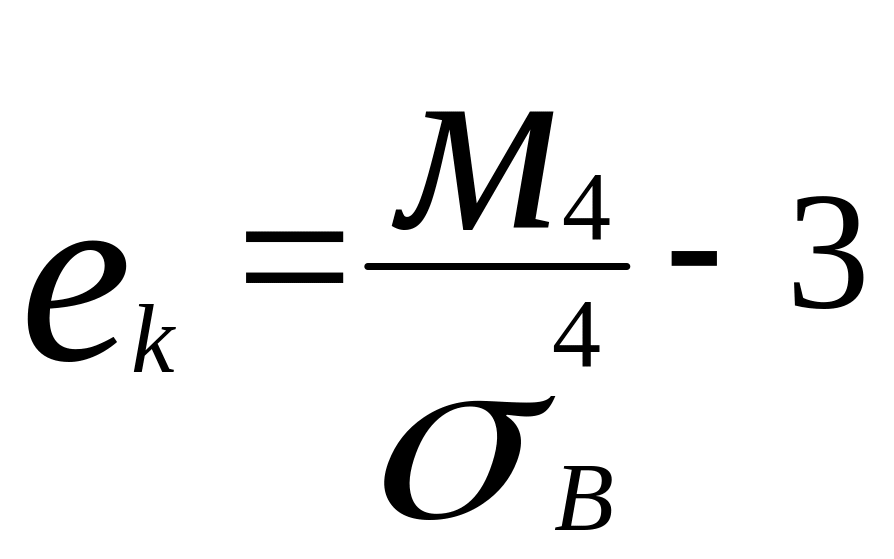-характеризует отклонение распределения случайных чисел от нормального распределения (остро или туповершинность распределения, асимметрия по вертикали); где центральный эмпирический момент четвертого порядка. Он вычисляется либо по формуле ,

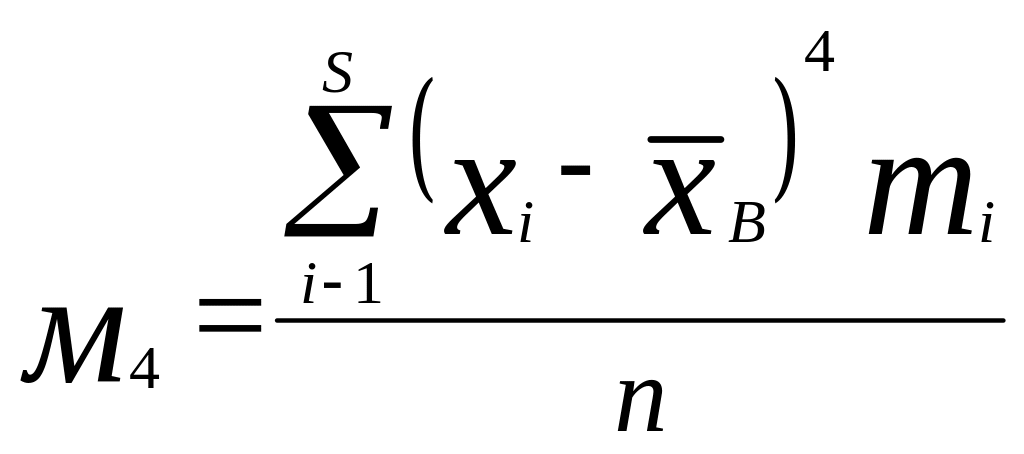либо по формле

.

11. Коэффициент вариации

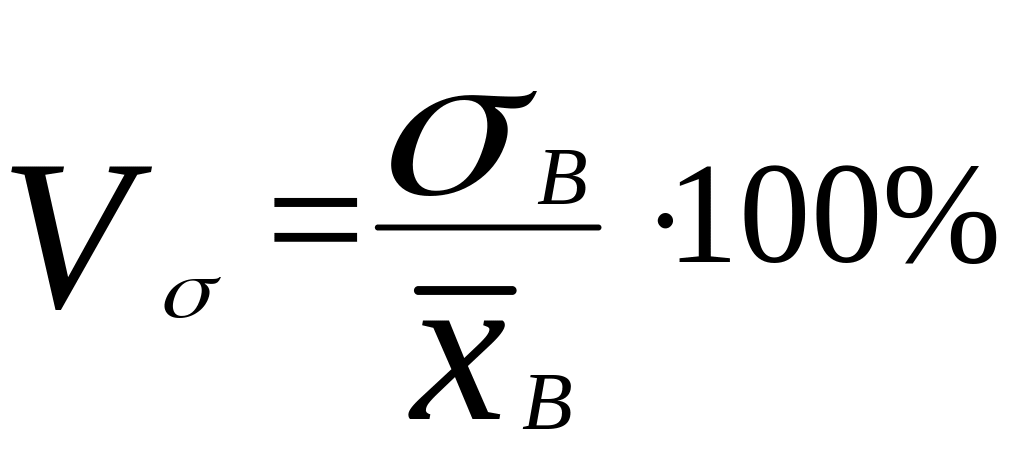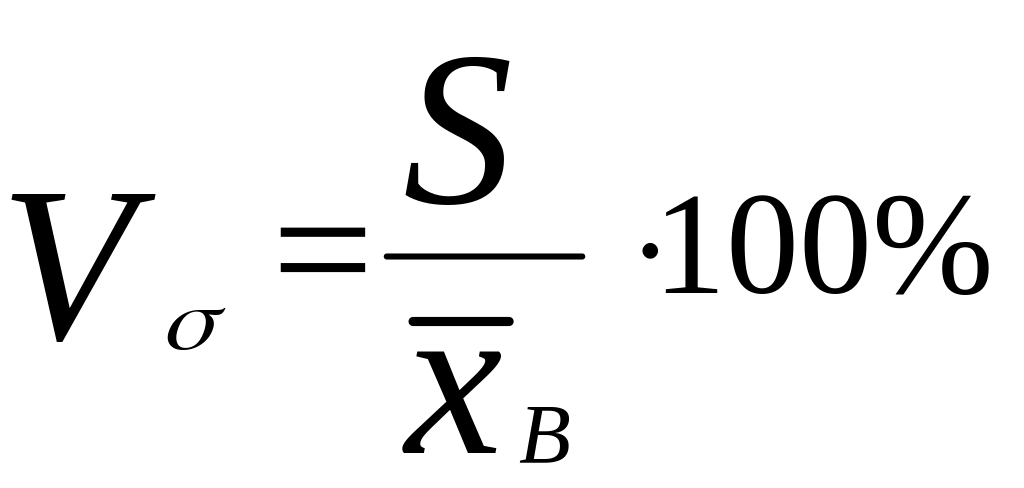, - характеризует меру вариации (относительной изменчивости) случайной величины.

Если - изменчивость незначительна;

Если - изменчивость средняя;

Если - изменчивость значительная.

Коэффициенты вариации дают относительную характеристику однородности явлений и процессов, они позволяют сравнивать степень вариации разных признаков.

Замечание. Для упрощения “ручных” расчетов, удобнее перейти от данных значений вариант к условным средним по формуле

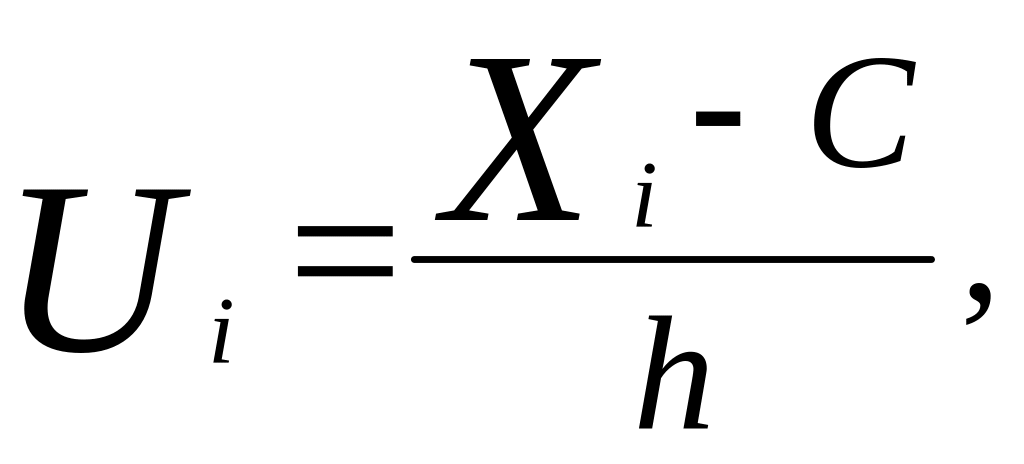где С- ложный нуль, равный значению (моды) в вариационном ряде распределения, которой соответствует наибольшее значение частоты т.е. в вариационном ряде. Тогда вариационный ряд примет вид

	….	-2	-1	0	1	2	…….
	….						…….
	….						…….

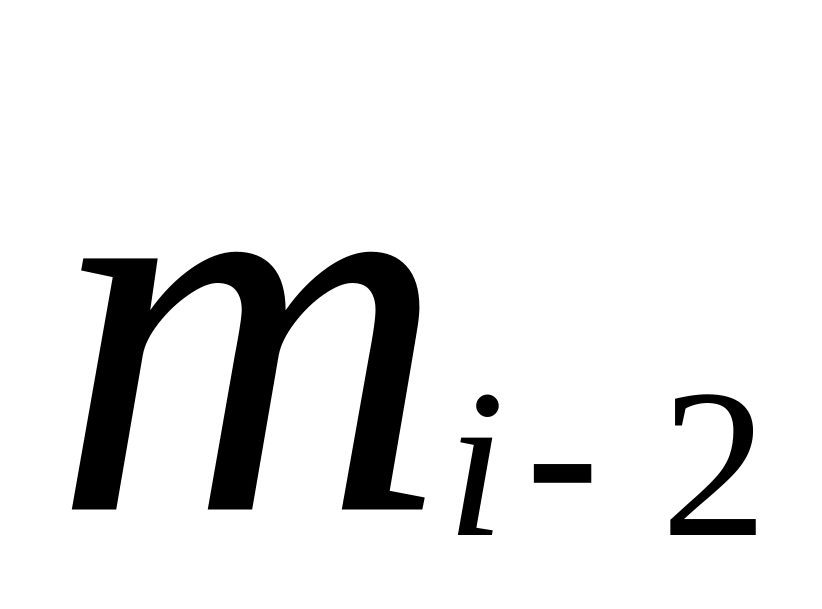
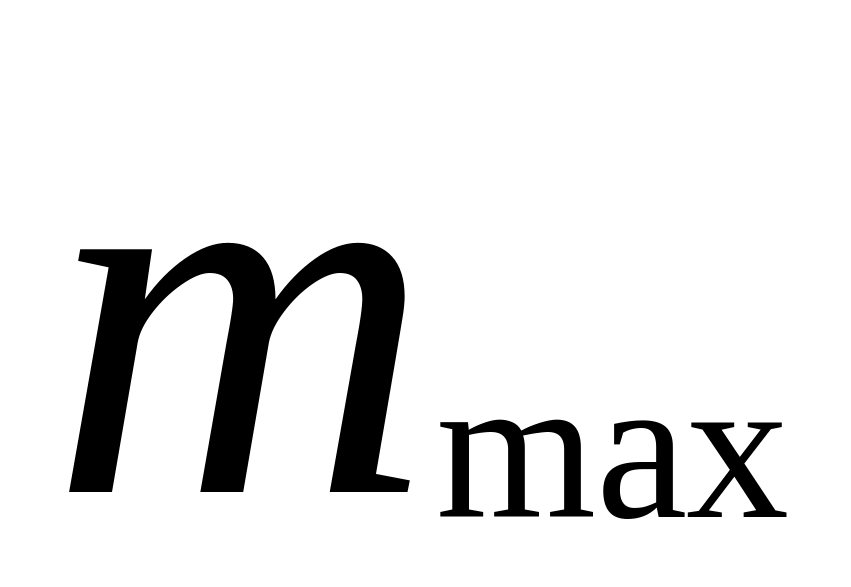
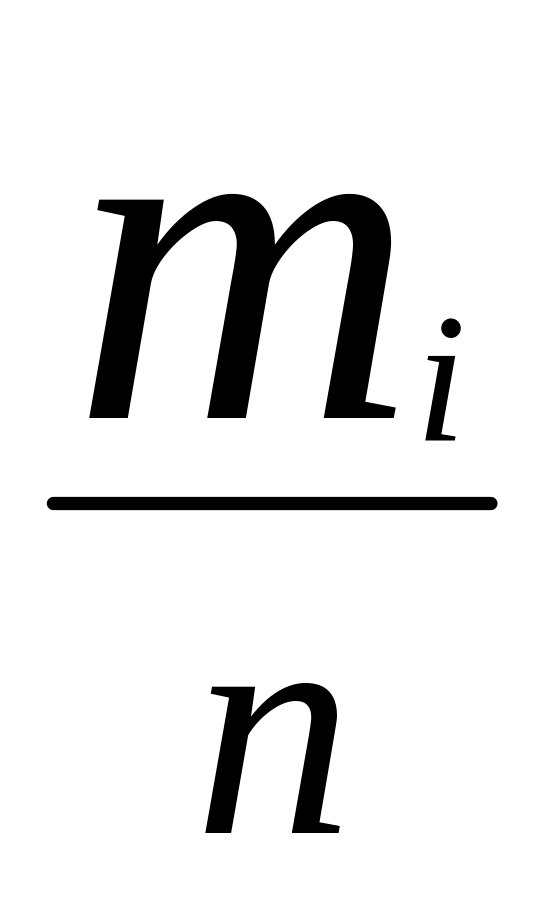
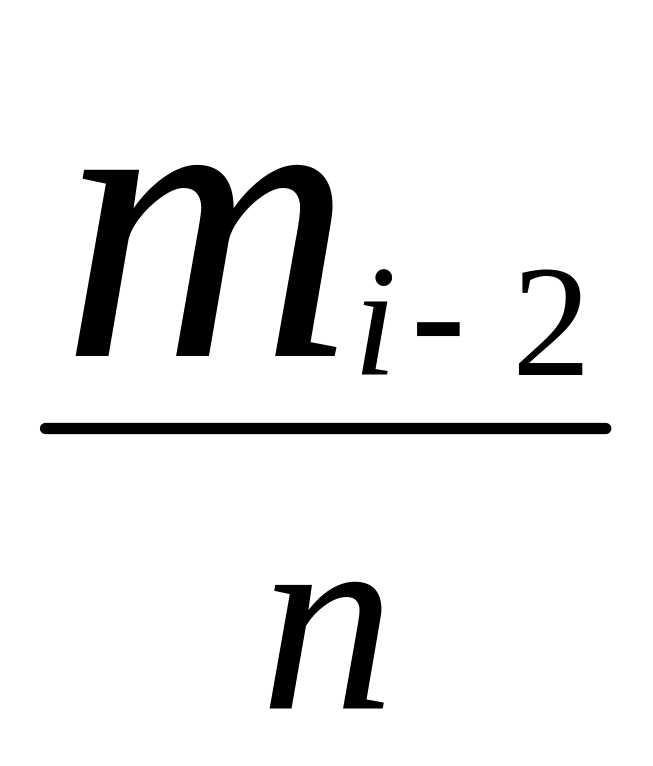
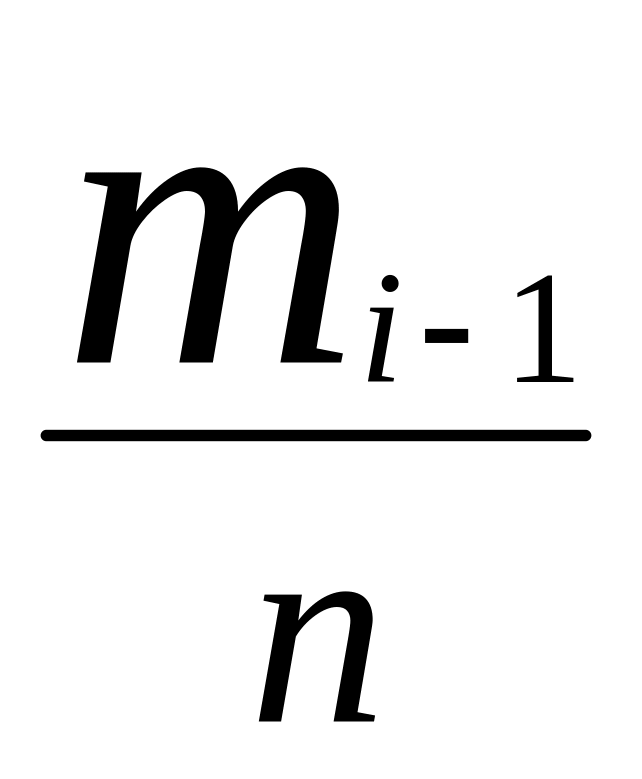
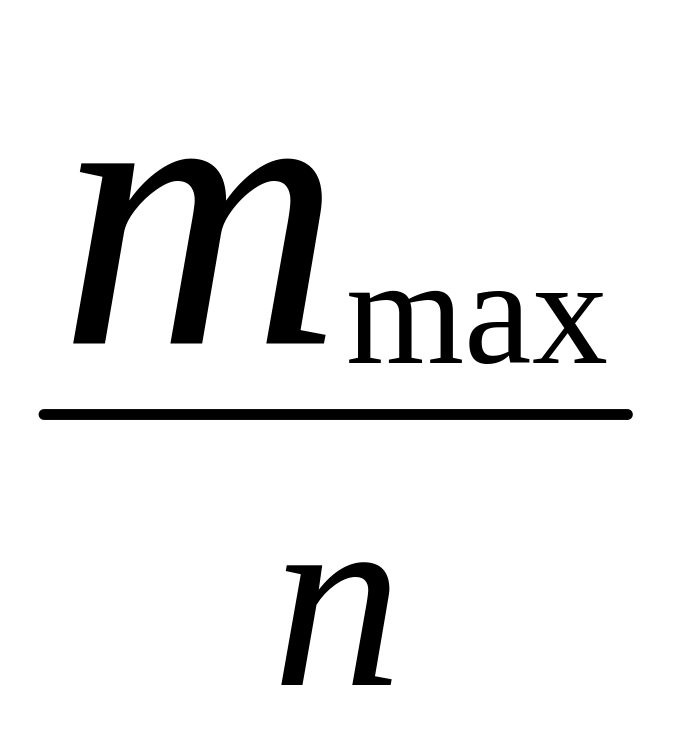
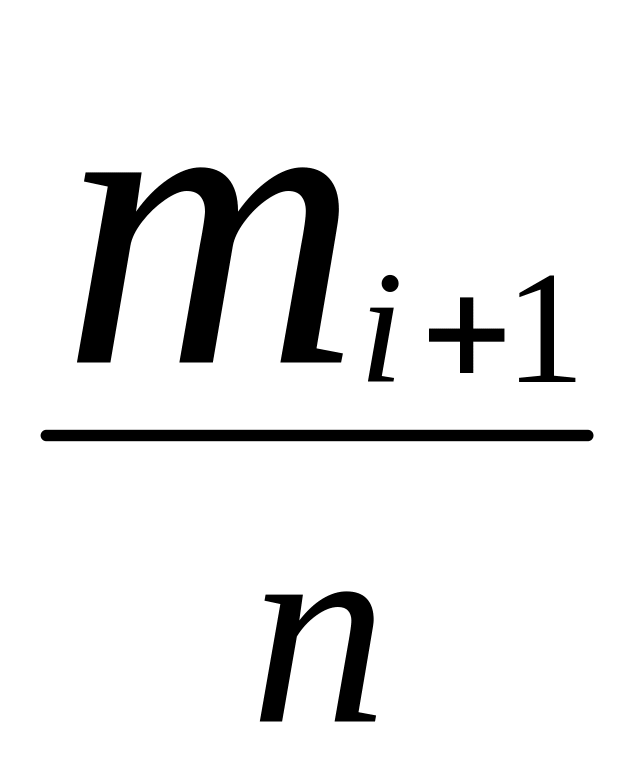
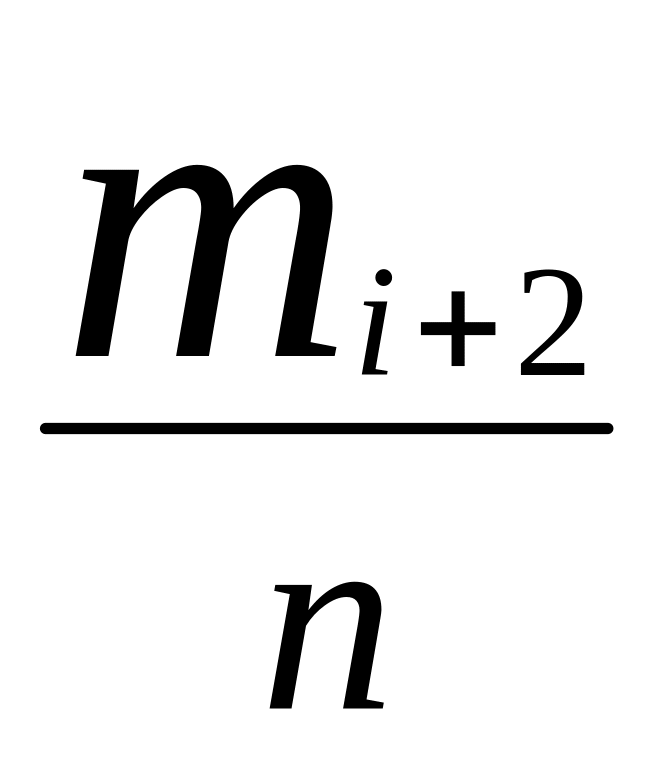
Числовые характеристики в условных вариантах вычисляются по известным, приведенным выше формулам с той лишь разницей, что вместо используется .

При обратном переходе от числовых характеристик с.в. к числовым характеристикам исходной переменной используются формулы:

Здесь использованы свойства математического ожидания, дисперсии и моментов более высоких порядков, когда с.в. X и Y независимы:

1)

2)

3)

4)

5)

6) т.к.

7)

Промежуточные расчеты при вычислении числовых характеристик удобнее провести в виде таблицы.

Этап 4. Вычисление доверительных интервалов числовых характеристик изучаемой случайной величины с заданной надежностью (вероятностью).

Числовые характеристики, вычисленные по случайной выборке из генеральной совокупности, лишь приближенно характеризуют истинные значения аналогичных характеристик изучаемой генеральной совокупности. Поэтому по вычисленным значениям необходимо определить те надежностные интервалы, которые будут накрывать истинные значения числовых характеристик генеральной совокупности с заданной вероятностью Отклонение выборочной характеристики (средней) от генеральной называется предельной ошибкой выборки Она определяется в долях средней ошибки с заданной вероятностью , т.е.

, (А)

где коэффициент доверия, зависящий от вероятности , с которой определяется предельная ошибка выборки; ошибка выборки (ошибка выборочной средней).

Надежностный интервал для генеральной средней имеет вид

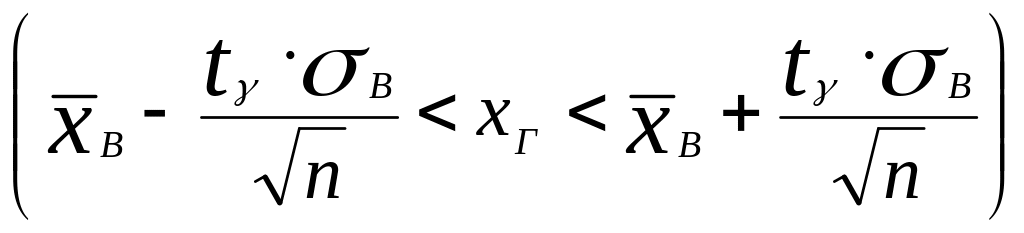, где среднее выборочное, - объем выборки, выборочное с.к.о, - значение аргумента функции Лапласа, при которой она равна , т.е. находится по таблице значений функции Лапласса из условия надежностная вероятность, выбирается исследователем. Значение , как правило, считается достаточным для большинства исследований. При этом предполагается, что распределение случайной величины , полученное суммированием исходных случайных венличин, распределенных по нормальному закону распределения, также распределена нормально.

Надежностный интервал с вероятностью накрывает генеральную среднюю .

Замечание. Если выборка мала ( ), то надежностный интервал для генеральной средней имеет вид

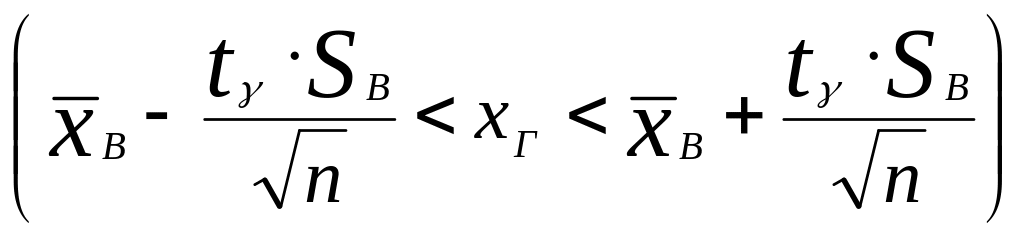, где исправленное выборочное среднеквадратическое отклонение, коэффициент доверия, число, взятое из таблицы Приложения (таблица 3) значений .

Надежностный интервал для среднего квадратического отклонения генеральной совокупности имеет вид , где исправленное выборочное среднее квадратическое отклонение, табличное значение критических точек (таблица 4 Приложения). Надежностный интервал для указывает с вероятностью на то, что эти отклонения могут принимать значения, находящиеся в пределах от до

Определение необходимого объема выборки

При разработке программы выборочного обследования одним из наиболее сложных является вопрос о том, сколько единиц изучаемой совокупности необходимо обследовать, т.е. об объеме выборки (см.[2]).

Из формулы предельной ошибки выборки (А) следует, что если задана предельная ошибка выборки , то объем выборки , обеспечивющий заданную точность, определяется по формуле

.

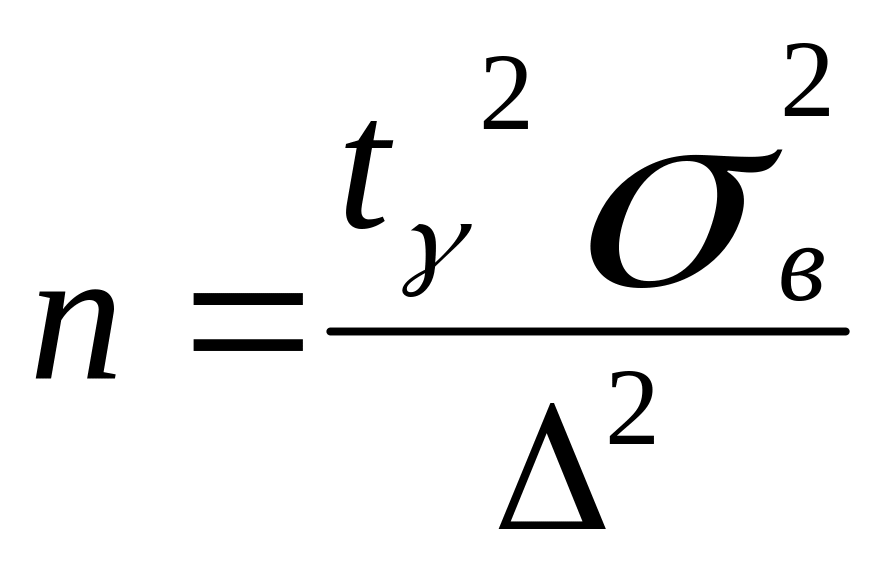Для определения необходимого объема выборки должны быть заданы предельная ее ошибка и вероятность того, что эта ошибка не превысит заданного предела. В соответствии с этой вероятностью по таблице Приложения находят коэффициент доверия .

Этап 5. Содержательная интерпретация результатов первичной обработки данных по условию задачи.

1. Оценка математического ожидания (среднее) , вычисленное по выборочным данным, представляет собой обобщенную характеристику всей совокупности значений в целом; являясь как бы точкой сгущений, характеризует центральное положение значений случайной величины в эмпирическом законе распределения (см. графики гистогаммы, полигоны частот и вероятностей). В реальной жизни мы наблюдаем чаще всего (с большей вероятности) те значения признака , которые близки к . - это оценка математического ожидания закона распределения с.ч. , т.е. это наиболее часто ожидаемое число.

2. Доверительный интервал 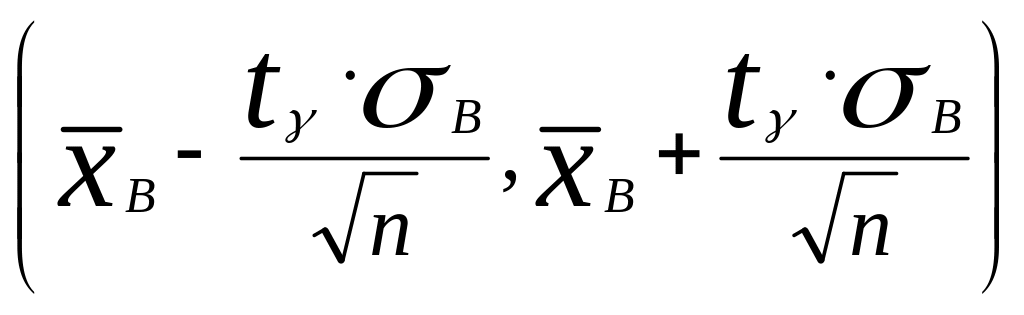указывает на то, что с вероятностью генеральная средняя изучаемой случайной величины заключена в найденном интервале.

3. Среднее квадратическое отклонение (с.к.о.) служит показателем о наиболее вероятном отклонении конкретной варианты признака от его среднего значения данной совокупности. С.к.о. измеряется в тех же единицах, что и варьирующий признак и исчисляется путем извлечения квадратного корня из дисперсии, т.е. как .

Основные значения, ядро вариационного ряда, содержится в интервале

или Отклонения от превосходящие по модулю возможны, но вероятность их уменьшается по мере удаления от .

Заметим, что если с.в. Х имеет нормальный закон распределения с параметрами и т.е. то практически достоверно, что ее значения заключены в интервале ( . Эта закономерность «известна как правила трех сигм». Нарушение «правила трех сигм» является событием практически невозможным, т.к. его вероятность весьма мала:

Надежностный интервал с вероятностью накрывает значение среднего квадратического отклонения генеральной совокупности.

4. Асимметрия указывает на нарушение симметрии распределения случайных чисел от среднего, наличие скоса. Если то наблюдается правосторонняя асимметрия (преимущественно значения случайных чисел больше чем среднее значение ); если то левосторонняя; если то распределение симметричное.

5. Эксцесс указывает на характер вершины распределения. Если то распределение островершинное; если то распределение пологое; если то оно совпадает со стандартным нормальным.

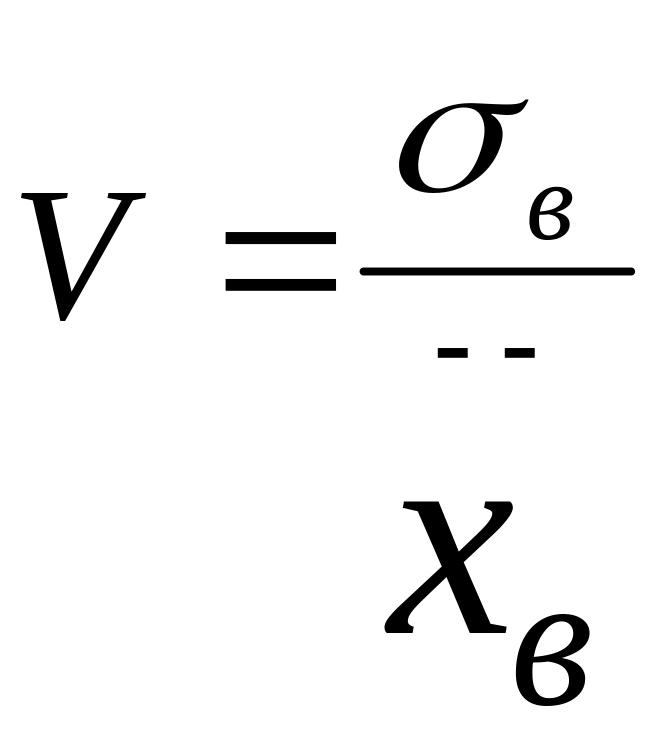
6. Коэффициент вариации - стандартное отклонение, выраженное в процентах к средней арифметической данной совокупности, т.е. . ( . 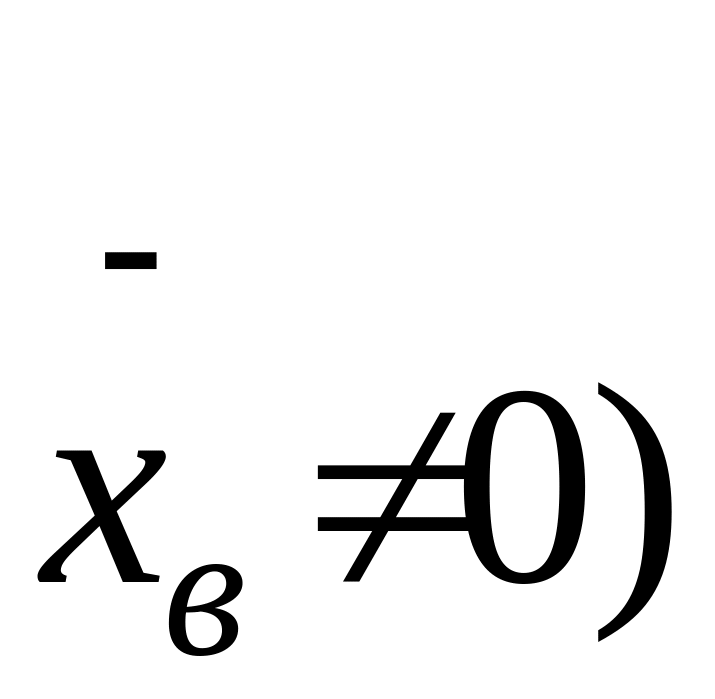Он является относительным показателем изменчивости с.в., дает относительную характеристику однородности явлений и процессов, позволяет сравнивать степень вариации разных признаков. Если то изменчивость считают незначительным, если то изменчивость считают средней, если то изменчивость значительная. Этот коэффициент, как показатель колеблемости, имеет смысл только при положительных значениях вариант. Если V>100%, то это является свидетельством неоднородности с.в. (признака).

Рассмотренные числовые характеристики необходимо сопоставлять с вариационным рядом, его графическим изображением и интерпретировать с учетом единиц измерения и содержания, указанных в условиях задачи.