7.3 Модель выбора птс с частичной взаимозаменяемостью станков

ПТС предназначена для отработки деталей n типов ( ); причем годовая программа деталей каждого типа равна N_k. Детали каждой k-й группы проходят некоторое число операций из набора . На каждой операции j_k из набора J_k можно использовать S_ij взаимозаменяемых станков I_j типов , различающихся производительностью, степенью автоматизации, стоимостью и затратами на эксплуатацию. Уточним, что на каждом i_j - м станке производится одна из операций маршрутного технологического процесса обработки деталей k - й группы . Станкоемкость обработки детали k - й группы на j - й операции i - м станком равна t_ijk, реальный годовой фонд времени i_j - го станка принимается в размере Т_эijK_иij, а затраты на его приобретение и эксплуатацию составляют С_ij.

Требуется определить оптимальную ПТС, т.е. число станков S_ij каждого типа на каждой операции. Модель является, как видно, развитием предыдущей (т.е. является цепью задач о назначениях).

Математическая модель описана следующим образом.

Критерий оптимальности

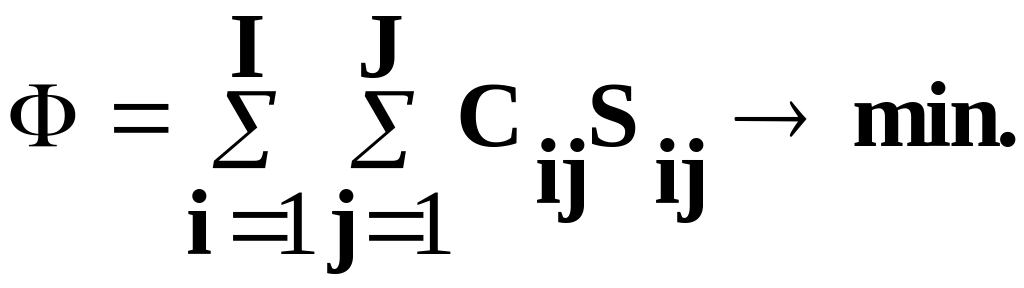
Ограничения: по использованию станков; по реальному годовому фонду времени; ограничения на переменные.

Дополнительно могут включаться ограничения: по дефицитности оборудования; по надежности системы.

Как и в предыдущем случае, условия задачи не запрещают дробление годовой производственной программы N_k по различным группам S_ij cтанков, а при введении ограничения по дефицитности предусматривают его.

Термин “частичная взаимозаменяемость станков” следует, таким образом, понимать в том смысле, что допускается взаимозаменяемость станков в пределах одной операции: для различных операций используются станки различных типов.

7.4 Модель выбора птс с взаимозаменяемостью технологических маршрутов обработки

Имеется в виду взаимозаменяемость маршрутов внутри каждой k-й группы деталей. Случай идентичности маршрутов по всем технологическим группам деталей по отношению к указанному является частным.

Итак, имеется n групп (типов) деталей ( ), годовая программа деталей каждого типа равна N_k. Для каждой k-й группы деталей возможна реализация M_k технологических маршрутов ( ). Станкоемкость обработки детали k-й группы i-м станком по i-му маршруту составляет t_ijk, реальный годовой фонд времени работы i-го станка равен Т_эiK_иi. Во всех технологических маршрутах обработки всех n групп деталей используются I типов станков ( ). В том или ином маршруте j при обработке той или иной детали k-й группы станок i может не использоваться ( ). Затраты на приобретение и эксплуатацию i-го станка составляют С_t. Имеется, таким образом, множество технологических маршрутов, соответствующим образом совмещенное с множеством обрабатываемых деталей. Требуется выбрать оптимальную ПТС, т. е. номенклатуру и число станков в совокупности с технологическими маршрутами обработки деталей всех n групп.

Математическая интерпретация модели выглядит следующим образом.

Критерий оптимальности

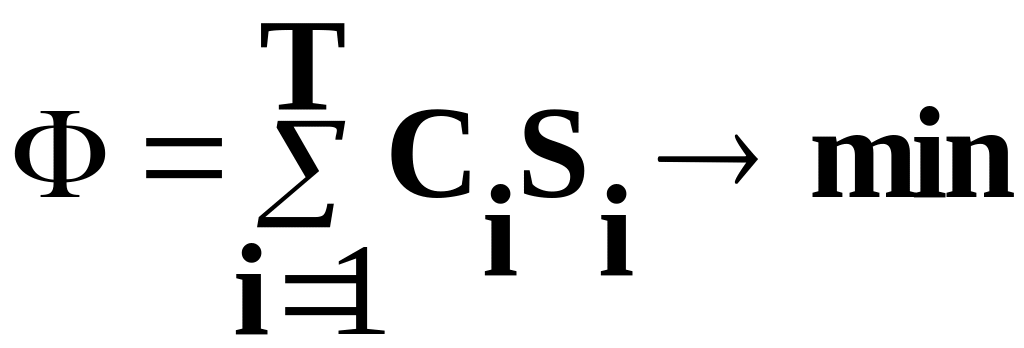
Ограничения: по технологическому маршруту; по производственной программе и реальному годовому фонду времени; ограничения на переменные. Аналогично предыдущим моделям могут быть учтены ограничения по дефицитности оборудования и надежности системы.

Анализ приведенных моделей показывает, что первая является частным случаем второй при J_k = 1, а вторая является частным случаем третьей при М_k = 1. Действительно, в модели с частичной взаимозаменяемостью станков для каждой детали k-го наименования реализуется один технологический маршрут. Однако вторая модель “разворачивается” в третью перебором всех возможных вариантов сочетаний станков по отдельным операциям и с формальной точки зрения представляется состоящей из соответствующего числа псевдомаршрутов. Таким образом, и с теоретической, и с практической точек зрения основной является третья модель. Эта модель имеет, вообще говоря, более широкое применение и пригодна для выбора структуры любого специального технологического комплекта оборудования в серийном производстве. Для задач дискретной оптимизации крайне необходимы, с одной стороны, не только точные, но и приближенные методы решения (как с оценкой отклонения от оптимума, так и без таковой), с другой - максимальный учет специфики решаемых задач. Методология, о которой идет речь, на наш взгляд, хорошо иллюстрирует эту мысль.

Основная масса описанных моделей относится к классу задач анализа. Одна из задач оптимального распределения ресурсов состоит в выборе, при котором требуется распределить механизмы S_i ( ) по видам работ N_k ( ) таким образом, чтобы суммарный эффект от их использования был бы максимален при условии I = n. Графически задача интерпретируется двудольным графом. Производительность механизма S_i при выполнении работы N_k равна П_ik ( ). Задача сводится к выбору такой последовательности элементов П_ik из матрицы

при которой суммарная производительность всех механизмов была бы максимальна. При этом из каждой строки и каждого столбца матрицы выбирается один элемент. Для решения задачи используется так называемый “венгерский” метод. Как видно, задача является частным случаем обобщенной задачи о назначениях (модель выбора ПТС с полной взаимозаменяемостью станков).

Модели определения состава оборудования проектируемых участков и цехов машиностроительных заводов. Описываются следующими условиями: при заданных вариантах выполнения на различных станках операций обработки деталей, закрепленных за цехом, необходимо выбрать такие станки и в таком количестве и так распределить операции обработки по этим станкам, чтобы при выполнении заданных ограничений затратная целевая функция приняла бы наименьшее значение. Модель представлена как задача ЦЛП, в которой часть переменных являются булевыми, а часть может принимать значения любых целых неотрицательных чисел.

Большая размерность задачи затрудняет применение точных методов. Предложен эвристический метод, разбитый на два этапа. На первом этапе для каждой j_k - й деталеоперации находится локально-оптимальный вариант закрепления ее за станком независимо от эффективности выполнения остальных деталеопераций. В полученном таким образом начальном условно-оптимальном решении некоторые станки могут оказаться существенно недогруженными. Второй этап предусматривает улучшение полученного начального решения путем направленного пошагового перераспределения деталеопераций по станкам с учетом выполнения всех деталеопераций и загрузки станков с возможным уменьшением числа последних.