
- •В помощь первокурснику
- •Аудиторные виды учебной деятельности Лекции
- •Практические занятия
- •Семинарские занятия
- •Лабораторные работы
- •Консультации
- •Работа на лекции
- •Ведение записей
- •Отдельные виды записей
- •Самостоятельная работа студентов
- •Доработка материала после лекции
- •Проработка лекционного материала
- •Подготовка к практическим занятиям
- •Подготовка к семинарским занятиям
- •Некоторые советы
- •Подготовка к сессии
- •Подготовка к экзамену во время сессии
- •Сдача экзамена
- •Ответ на экзамене
- •11. В сессии, как и в длительных состязаниях, нужна выдержка и воля к победе! Не падайте духом при неудачах! Стремитесь к победе! вопросы экзамена
- •Памятка
- •Необходимые и достаточные условия
- •Список рефератов
- •Основные направления научно-исследовательской работы студентов- электриков
- •Примеры учебно-профессиональных задач для создания проблемных ситуаций и реферативных работ по емд (естественно- математических дисциплин)
- •Решение задач
- •2. Элементы векторНой алгебРы
- •Самостоятельная работа
- •Самостоятельная работа
- •3. Аналитическая геометрия
- •Найдем координаты точки м(хм;ум) – пересечения высоты cd и медианы ве, решив систему их уравнений методом Крамера:
- •Самостоятельная работа
- •4. Математический анализ
- •Самостоятельная работа
- •Физическая и техническая интерпретация математических понятий
- •2.1. Сущность физико-математических понятий
- •1. Изучение условия.
- •2. Выработка плана решения.
- •3. Реализация плана.
- •4. Проверка и анализ решения.
- •1. Ознакомление с условием задачи и его анализ
- •2. Составление плана решения задачи
- •III. Осуществление решения задачи
- •IV. Проверка результата решения задачи
- •V. Оценка практической значимости решения задачи
- •VI. Рефлексия (ретроспективный анализ) деятельности по решению задачи
- •I. Ознакомление с условием задачи и его анализ
- •II. Составление плана решения задачи
- •III. Осуществление решения
- •IV. Проверка результата решения задачи
- •V. Оценка практической значимости решения задачи
- •VI. Рефлексия деятельности по решению задачи
- •Эвристический план решения прикладной задачи
- •Понимание постановки задачи
- •Приложения математики
- •Системы уравнений
- •Вектора
- •Б олее сложные задачи
- •Аналитическая геометрия
- •Упражнения
- •Некоторые задачи, решаемые при помощи уравнения прямой линии
- •Упражнения
- •Функция и предел
- •Литература по прикладные задачи
Самостоятельная работа
Задание1: Выполнить линейные операции над векторами.
Д
 аны
векторы:
аны
векторы:
![]()
Найти: 1)![]() ;
2)
;
2)
![]() ; 3)
; 3)![]() ;
;
![]() .
.
Даны векторы:
 Найти: 1)
Найти: 1)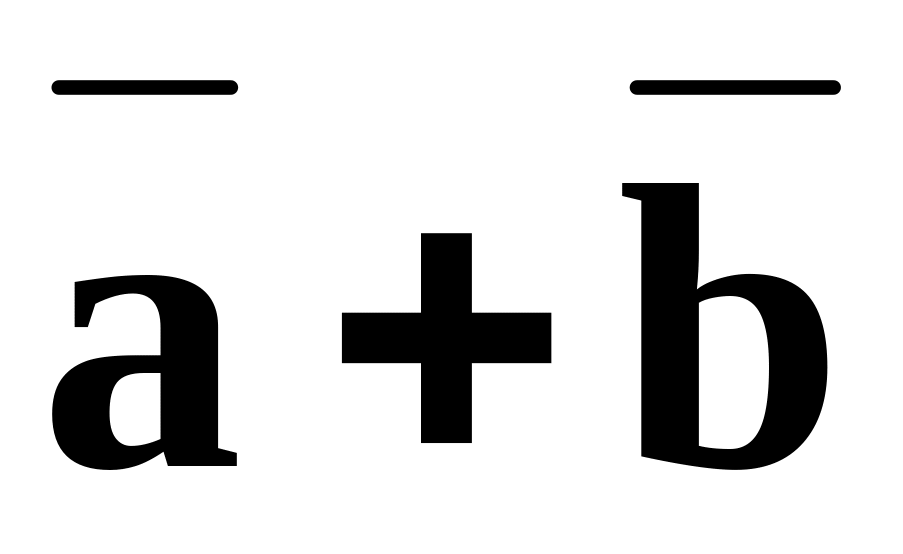 ;
2)
; 3)
;
.
;
2)
; 3)
;
.
Даны три точки А(-1;1), В(3;-2), С(2;4). Найти векторы 1)
 3)
3)
Найти равнодействующую трех сил:

 и построить векторы.
и построить векторы.
ЗАНЯТИЕ 2.
Тема: ОПРЕДЕЛЕНИЕ МОДУЛЯ ВЕКТОРА И ЕГО НАПРАВЛЕНИЯ В ПРОСТРАНСТВЕ. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Пример 1. Даны на плоскости
точки А(-2;3) и В(2;7). Найти 1) вектор![]() ,
2) модуль
,
2) модуль
![]() ,
3) направляющие косинусы, 4) построить
вектор
.
,
3) направляющие косинусы, 4) построить
вектор
.
Решение:
найдем координаты вектора :
![]() выпишем его координаты АВх
= 4, АВу= 4;
выпишем его координаты АВх
= 4, АВу= 4;
вычислим модуль по формуле:
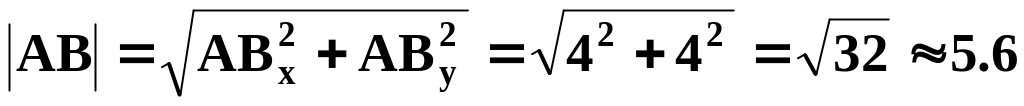 ;
;вычислим направляющие косинусы по формулам:


4) построим вектор
![]() по его координатам
по его координатам
и координатам точек А(-2;3) и В(2;7).
Пример 2. Найти проекцию
вектора
![]() на вектор
на вектор
![]() .
.
Решение:
![]()
Пример 3. Определить
работу по перемещению тела из точки
А(2;-4;1) в точку В(3;2,-1) под действием
сил:
![]() .
.
Решение:
Найдем вектор перемещения тела:
![]() ;
;
Вычислим равнодействующую трех сил:
![]() .
.
Определим работу по перемещению тела, как скалярное произведение вектора равнодействующей силы и вектора перемещения:
А=![]() =
4*1+6*6+(-2)*3=34 ед. работы.
=
4*1+6*6+(-2)*3=34 ед. работы.
Пример 4. Вычислить площадь треугольника с вершинами: А(3;1;2), В(4;3;5) и С(-8;2;3).
Решение:
Так как
![]() ,
,
Найдем координаты векторов:
![]()
![]() ;
;
Определим векторное произведение:
 =
=![]()
Вычислим площадь треугольника:
![]() кв.
ед.
кв.
ед.
Самостоятельная работа
Задание 1.
Даны на плоскости точки М(3;-2) и N(-1;3). Найти 1) вектор
 ,
2) модуль
,
2) модуль
 ,
3) направляющие косинусы, 4) построить
вектор
.
,
3) направляющие косинусы, 4) построить
вектор
.Найти проекцию вектора
 на вектор
на вектор
 .
.
Определить работу по перемещению тела из точки А(1;3;-2) в точку В(2;-1;4) под действием сил:
 .
.
Вычислить площадь треугольника с вершинами: А(-1;2;4), В(1;3;6) и С(-3;5;2).
3. Аналитическая геометрия
ЗАНЯТИЕ 1 и 2.
Тема: ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Пример 1. Даны две точки А(-1;2) и В(1;5). Найти: 1) длину АВ; 2)С(хс;ус) –середину АВ; 3)записать уравнение прямой АВ, 4)найти k- угловой коэффициент и b-отрезок оси Оу, отсекаемый прямой.
Решение:
Длина АВ=
 ;
;Координата С(хс;ус) –середины АВ найдем по формуле:
![]() .
С(0;3.5) –середина АВ;
.
С(0;3.5) –середина АВ;
Запишем уравнение прямой, проходящей через две заданные точки А и В:
 .
.
Подставим координаты точек А(хА
= -1, уА = 2) и В(хВ
= 1, уВ = 5) в это уравнение:
![]() 2(у
- 2) = 3(х + 1)
2(у
- 2) = 3(х + 1)
![]() 2у - 4 = 3х + 3
2у - 4 = 3х + 3
![]() -3х
+ 2у - 7 = 0. Получили общее
уравнение прямой АВ.
-3х
+ 2у - 7 = 0. Получили общее
уравнение прямой АВ.
Преобразуем полученное уравнение в уравнение прямой с угловым коэффициентом вида: у=кх+b. Выразим у через х: 2у=3х+7 /:2 у =
 (х
+7)
(х
+7)
 - это уравнение прямой АВ с угловым
коэффициентом, где
- это уравнение прямой АВ с угловым
коэффициентом, где
 - угловой коэффициент АВ, а
b=
- угловой коэффициент АВ, а
b= --отрезок
оси Оу, отсекаемый прямой.
--отрезок
оси Оу, отсекаемый прямой.
Угловой коэффициент прямой, проходящей
через две заданные точки А и В
можно рассчитать по формуле:
![]() .
.
Пример 2. Записать уравнение прямых, проходящих через точку С(-4;2) параллельно и перпендикулярно прямой, проходящей через точки А(3;-4) и В(2 -2).
Решение:
Найдем угловой коэффициент для прямой АВ:
![]() .
.
Найдем угловой коэффициент для прямой
 из условия параллельности:
из условия параллельности:
 .
.Найдем угловой коэффициент для прямой
 из условия перпендикулярности:
из условия перпендикулярности: .
.Запишем уравнения прямых
 и
и
 ,
используя уравнение прямой, проходящей
через заданную точку С с заданными
угловыми коэффициентами:
,
используя уравнение прямой, проходящей
через заданную точку С с заданными
угловыми коэффициентами:
![]() ;
;
![]() .
.
Пример 3. Дан треугольник с вершинами А(-8;3), В(-6;0), С(6;-5). Составить уравнения 1) стороны АС, 2) высоты CD и 3) медианы ВЕ. 4) Найти координаты точки М(хм;ум) – пересечения высоты CD и медианы ВЕ.
Решение:
С
 оставим
уравнение стороны АС, используя
уравнение прямой, проходящей через две
заданные точки:
оставим
уравнение стороны АС, используя
уравнение прямой, проходящей через две
заданные точки:
![]()
![]()
![]() 14*(у - 3)=(-8)*(х + 8)
14*(у - 3)=(-8)*(х + 8)
8х + 14у + 22=0 – искомое уравнение стороны АС;
Высота CD
 АВ
АВ
 .
.
Найдем
![]() и
и
![]()
Составим уравнение высоты CD, используя
уравнение прямой, проходящей через
заданную точку С(6;-5)
с заданным угловым коэффициентом
![]() :
:
![]() -
искомое уравнение высоты CD
с угловым коэффициентом.
Запишем его в общем виде, умножив обе
части уравнения на 3: 2х-3у-27=0-
общее уравнение высоты CD;
-
искомое уравнение высоты CD
с угловым коэффициентом.
Запишем его в общем виде, умножив обе
части уравнения на 3: 2х-3у-27=0-
общее уравнение высоты CD;
Медиана ВЕ проходит через середину стороны АС. Найдем координаты Е(хЕ;уЕ)-середины отрезка АС по формулам:
 .
Е (-1;-1)
- середина стороны АС.
.
Е (-1;-1)
- середина стороны АС.
Составим уравнение медианы ВЕ, используя уравнение прямой, проходящей через две заданные точки:
![]()
![]()
![]() 5у =-х-6
5у =-х-6
х + 5у + 6=0 – искомое уравнение медианы ВЕ;
