Лабораторна робота №15 Використання excel для рішення прикладних задач. Задачі на оптимізацію.

Мета роботи: Освоїти навики роботи у MS EXCEL з аналізу даних, навчитись розв’язувати типові завдання за допомогою інструменту «Поиск решения»

Теоретичній матеріал: повторити використання функцій у формулах, обчислення за формулами, використання інструменту «Подбор параметра» і формули для роботи з масивами.

ЗАВДАННЯ ДО РОБОТИ

1. Розв’язування задач на оптимізацію.

Інструмент «Поиск решения» дозволяє знайти оптимальний розв’язок сформульованої задачі. Застосовується для розв’язку задач оптимізації, які часто зустрічаються у економіці. Підключають цей інструмент з пункту меню Сервис/Поиск решения. Якщо у пункті меню Сервис немає цього інструментту, його треба до установити – Сервис/Надстройки/Поиск решения/Оk.

Математична модель задачі містить формулу цільової функції, для якої треба знайти оптимальне значення (максимальне, або мінімальне, або рівне де якому конкретному числу), ця формула має посилатись на ряд змінюваних комірок. Математична модель також містить задані обмеження «ограничения» у вигляді логічних виразів, які задають умови для обмеження області пошуку розв’язку. Задача полягає в тому, щоб змінюючи початкові значення в деякому діапазоні комірок знайти такі, що відповідають оптимальному значенню цільової функції та задовольняють усі обмеження.

Якщо розв’язку не існує, система обмежень не сумісна, тоді з’являється повідомлення «Поиск не может найти подходящего решения». Якщо функція мети не обмежена, тоді видається повідомлення «Значение целевой функції не сходится». Якщо розв’язок знайдено можна або зберегти знайдені значення або відновити попередні значення, результати пошуку відображаються у відповідних комірках таблиці аналогічно при пошуку розв’язку за допомогою «Подбора параметра». «Поиск решения» надає можливість використовувати одночасно декілька змінюваних параметрів (до 200) тоді як «Подбор параметра» тільки один.

1. Розв’язати економічну задачу: Скласти такий план випуску продукції, щоб отримати максимальний прибуток від ії реалізації, якщо відомо, що:

• прибуток від продукції П1 становить 40 грошових одиниць;

• прибуток від продукції П2 становить 30 грошових одиниць;

• на виготовлення одиниці продукції П1 необхідно витратити 5 одиниць сировини С1, 2 одиниці С2 і 4 одиниці С3;

• на виготовлення одиниці продукції П2 необхідно витратити 6 одиниць сировини С1, 6 одиниці С2 і 2 одиниці С3;

• Запаси сировини С1 дорівнюють 30 одиниць;

• Запаси сировини С2 дорівнюють 24 одиниць;

• Запаси сировини С1 дорівнюють 20 одиниць;

У стислому вигляді умови такої задачі прийнято записувати так:

	П1	П2	Запаси
С1	5	6	30
С2	2	6	24
С3	4	2	20
Прибуток	40	30	max

1. Складемо математичну модель задачі: через Х1 позначимо кількість одиниць продукції П1, через Х2 – кількість одиниць продукції П2. Тоді кількість витраченої сировини на виготовлення усій продукції буде:

5x₁+6x₂<=30 – сировини С1

2x₁+6x₂<=24 – сировини С2

4x₁+2x₂<=20 – сировини С3

При цьому x₁>=0, x₂>=0, цілі числа.

Цільова функція визначається як F=40x₁+30x_2, треба підібрати такі x₁ та x₂, щоб функція мала максимальне значення.

1.1.2. Спроектуємо розрахункову таблицю на робочому аркуші Excel

	A	B	C	D	E	F
1		П1	П2	F max
2	кількість	4	2	=B3*B2+C3*C2
3	прибуток	40	30
4
5	обмеження
6	С1	5	6	=B6*B2+C6*C2	<=	30
7	С2	2	6	=B7*B2+C7*C2	<=	24
8	С3	4	2	=B8*B2+C8*C2	<=	20

Для того щоб розв’язати рівняння, в комірки B2:C2 занесемо початкові наближені значення змінних x₁ та x₂, в комірки D6:D8 – формули витрати сировини, це формули обмеження, в комірку D2– формулу знаходження цільовій функції. або у іншому вигляді:

	A	B	C	D	E	F
1		П1	П2	F max
2	кількість	4	2	220
3	прибуток	40	30
4
5	обмеження
6	С1	5	6	32	<=	30
7	С2	2	6	20	<=	24
8	С3	4	2	20	<=	20

1.1.3. Підключаємо Сервис /Поиск решения.

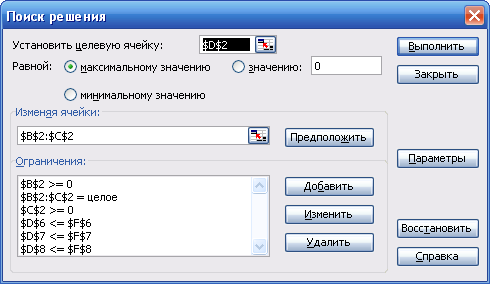
У вікні, що з’явиться на екрані, послідовно вказуємо:

• Установить целевую ячейку – вказати адресу комірки, де знаходиться цільова функція, D2

• Равной максимальному значению

• Изменяя ячейки – вказати діапазон адрес комірок де знаходяться початкові наближені значення змінних x₁ та x₂, B2:C2

• Ограничения /Добавить

• У вікні діалогу Добавление ограничения послідовно вказати усі обмеження:

  1. Ссылка на ячейку – адреса комірки, значення якої повинно задовольняти задане обмеження, наприклад для першого обмеження D6,

  2. відкрити список обмежень та вибрати потрібний знак – <=,

  3. Ограничение – адреса комірки, де задано значення обмеження, наприклад для першого обмеження F6,

• Якщо виникає потреба у зміні або вилученні певних обмежень тоді слід скористатися кнопками Изменить або Удалить

• можна установити максимальний час та максимальну кількість ітерацій на вкладці Параметры

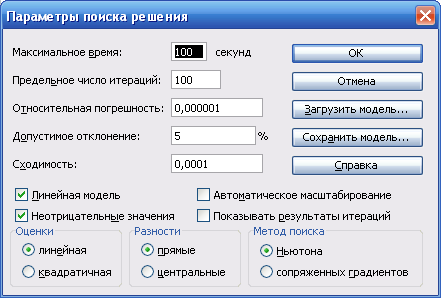
• Після того як усі обмеження задані потрібно натиснути кнопкуВыполнить

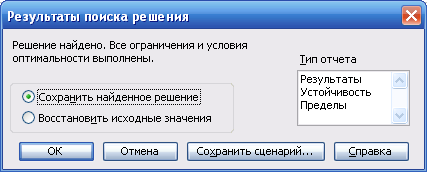
1.1.4. Після виконання операції Поиск решения на екрані в комірці B2:C2 одержуємо результат для х₁ та х₂, який задовольняє усім заданим обмеженням:

	П1	П2	F max
кількість	5	0	200
прибуток	40	30
обмеження
С1	5	6	25	<=	30
С2	2	6	10	<=	24
С3	4	2	20	<=	20

1.1.5. Можна зберегти знайдені Результати поиска решения як окремий сценарій, задавши його ім’я, та порівняти з іншими розв’язками задачі для інших значень обмежень, наприклад для даної задачі, вочевидь, що для максимального прибутку слід збільшити запаси сировини С1.

1.1.6. З отриманих результатів можна зробити висновок: для того щоб отримати найбільший прибуток при наявних ресурсах, підприємство повинно виготовляти 5 одиниць продукції П1 та 0 одиниць продукції П2. При цьому прибуток складатиме 200 одиниць прибутку.