
- •Кафедра высшей и прикладной математики
- •1.1. Предел последовательности
- •1.2. Предел функции
- •Геометрическая интерпретация. Пусть дан график функции , имеющей предел при , равный (рис.2).
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов
- •1.3. Раскрытие неопределенностей
- •1.4. Первый замечательный предел
- •1.5. Второй замечательный предел
- •2.1. Понятие производной функции
- •Формулы дифференцирования
- •2.2. Производная сложной функции
- •Пример. Найти производную функции .
- •2.3. Дифференцирование неявной функции
- •Признаки возрастания и убывания функции
- •3.1. Экстремум функции
- •3.2. Точки перегиба График функции называется выпуклым на интервале , если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
- •На интервале кривая выпукла , а на интервале – вогнута . Таким образом, при переходе через точку вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты .
- •3.3. Асимптоты
- •3.4. Общая схема исследования функции и построение ее графика
- •4.1. Первообразная функция и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •4.2. Непосредственное интегрирование
- •4.3. Интегрирование методом замены переменной (метод подстановки)
- •4.4. Интегрирование по частям
- •4.5. Интегрирование рациональных дробей
- •4.6. Интегрирование тригонометрических функций
- •5.1. Понятие определенного интеграла
- •Основные свойства определенного интеграла
- •5.2. Формула Ньютона-Лейбница
- •5.3. Методы интегрирования
- •7.1. Уравнение с разделяющимися переменными
- •7.2. Однородные дифференциальные уравнения первого порядка
- •7.3. Линейные дифференциальные уравнения
- •7.4. Дифференциальные уравнения второго порядка
- •7.5. Дифференциальные уравнения второго порядка с постоянными коэффициентами
- •8.1. Необходимый признак сходимости числового ряда
- •8.2. Достаточные признаки сходимости знакоположительных рядов
- •8.3. Знакочередующиеся ряды
- •Обобщенный признак Даламбера сходимости степенного ряда Для степенного ряда , где , составим предел модуля отношения последующего члена ряда к предыдущему
- •ЛиТература
Признаки возрастания и убывания функции
Следующая теорема выражает важный для практических целей признак строгого возрастания и строгого убывания функции и указывает правило для определения интервалов, на которых функция возрастает и убывает (интервалов монотонности функции).
Теорема. |
(достаточный признак возрастания и убывания функции на интервале)
Если во
всех точках некоторого интервала
первая производная
Если же
во всех точках некоторого интервала
первая производная
|
Правило. Для определения интервалов строгого возрастания и строгого убывания функции следует решить неравенства:
и .
Пример. Найти интервалы монотонности функции
![]() .
.
Решение.
Областью определения данной функции
является вся ось
![]() .
Находим производную
.
Находим производную
![]() .
Чтобы найти интервалы возрастания
функции, решим неравенство
.
Чтобы найти интервалы возрастания
функции, решим неравенство
![]() или
или
![]() ;
чтобы найти интервалы убывания функции,
решим неравенство
;
чтобы найти интервалы убывания функции,
решим неравенство
![]() .
Корни квадратного трёхчлена
.
Корни квадратного трёхчлена
![]() равны 1 и 3, поэтому распределение знаков
квадратного трехчлена имеет вид
равны 1 и 3, поэтому распределение знаков
квадратного трехчлена имеет вид
+ – +

1 3
Следовательно, на
интервалах
![]() и
и
![]() функция возрастает, а на интервале
функция возрастает, а на интервале
![]() функция убывает.
функция убывает.
3.1. Экстремум функции
Если для всех значений
из некоторой окрестности точки
![]() выполняется неравенство
выполняется неравенство
![]() ,
то
называют точкой локального максимума
функции
,
то
называют точкой локального максимума
функции
![]() ,
а
,
а
![]() – локальным максимумом функции. Если
для всех значений
из некоторой окрестности точки
выполняется неравенство
– локальным максимумом функции. Если
для всех значений
из некоторой окрестности точки
выполняется неравенство
![]() ,
то
называют точкой локального минимума
функции
,
а
– локальным минимумом функции. Минимумы
и максимумы функции называют ее
экстремумами.
,
то
называют точкой локального минимума
функции
,
а
– локальным минимумом функции. Минимумы
и максимумы функции называют ее
экстремумами.
Необходимый и достаточный признаки экстремума функции дают следующие две теоремы
ТЕОРЕМА 1 |
(необходимый признак экстремума)
Если точка
|
Эта теорема имеет простую геометрическую интерпретацию.

![]()
![]()
Рис. 4 Рис. 5 Рис. 6
На рис. 4 касательная
к графику функции
в точке
![]() –
точка экстремума – параллельна оси
–
точка экстремума – параллельна оси
![]() ,
т.е. угловой коэффициент (а это и есть
производная) равен нулю.
,
т.е. угловой коэффициент (а это и есть
производная) равен нулю.
На рис. 5 касательная в точке экстремума перпендикулярна оси , на рис. 6 касательная в точке с абсциссой не существует. В обоих случаях производная в точке не существует.
Точки, в которых первая производная равна нулю, а также, в которых она не существует, но функция сохраняет непрерывность, называются критическими.
Следует
уяснить, что указанный признак экстремума
является только необходимым, но
отнюдь не достаточным: производная
функции может быть равна нулю или не
существовать не только в тех точках, в
которых функция достигает экстремума.
Например,
производная функции
![]() равна нулю в любой точке, но экстремума
у этой функции нет (рис. 7). Поэтому,
определив критические точки, в которых
функция может достигать экстремума,
надо каждую из точек в отдельности
исследовать на основании достаточных
условий существования экстремума.
равна нулю в любой точке, но экстремума
у этой функции нет (рис. 7). Поэтому,
определив критические точки, в которых
функция может достигать экстремума,
надо каждую из точек в отдельности
исследовать на основании достаточных
условий существования экстремума.

![]()
0
Рис. 7
ТЕОРЕМА 2 |
(достаточный признак экстремума) Если при переходе через критическую точку производная меняет знак, то критическая точка является точкой экстремума. Это точка максимума, если производная меняет знак с плюса на минус, и точка минимума, если производная меняет знак с минуса на плюс. |
Пример.
Исследовать на экстремум функцию
![]() .
.
Решение.
Область определения
 .
.Находим критические точки, для чего найдем производную
 и приравняем ее к нулю
и приравняем ее к нулю
 .
Отсюда
.
Отсюда
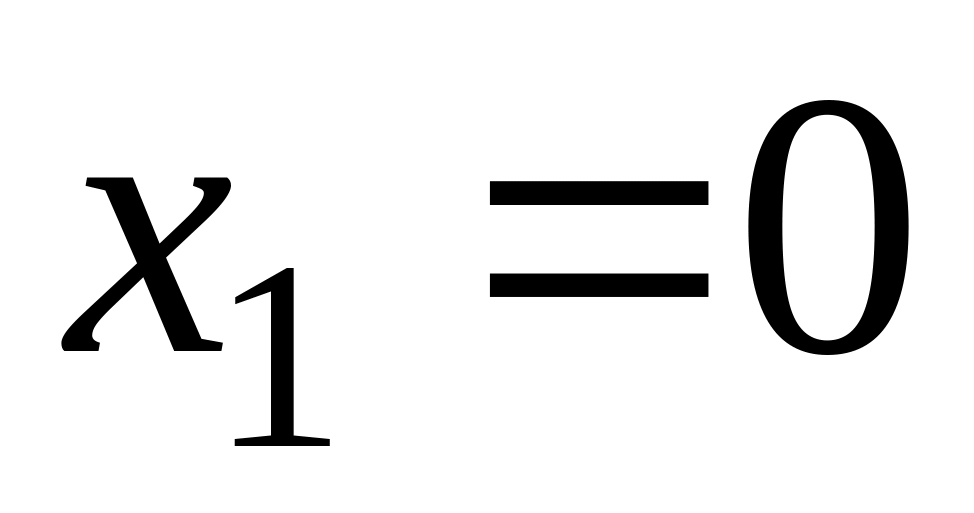 ,
,
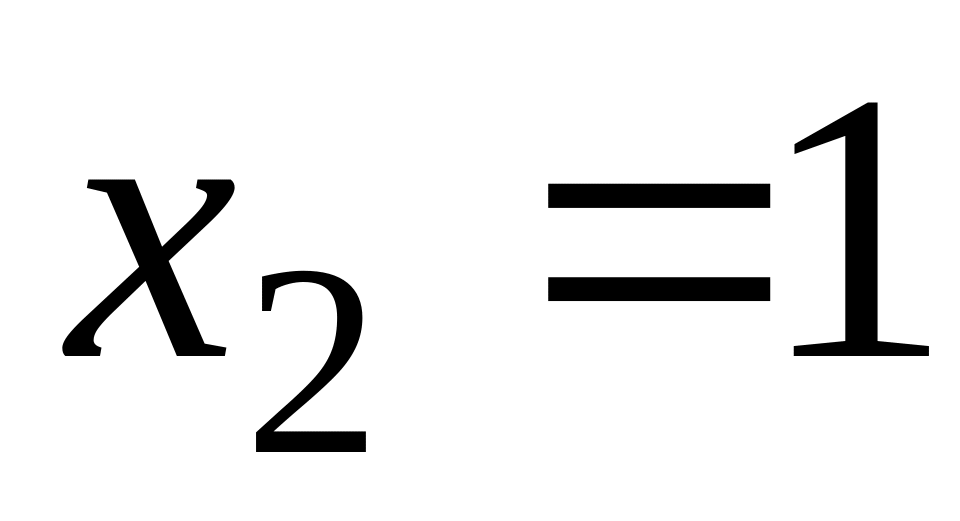 ,
,
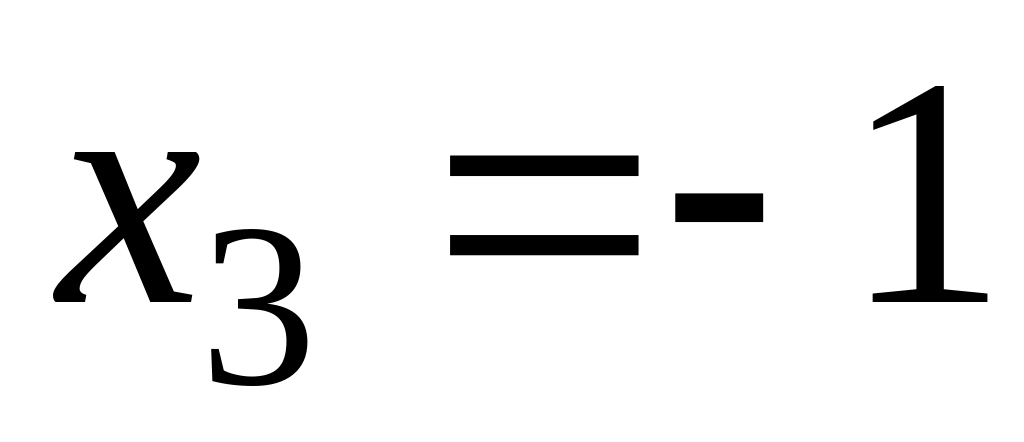 .
Точек, где
.
Точек, где
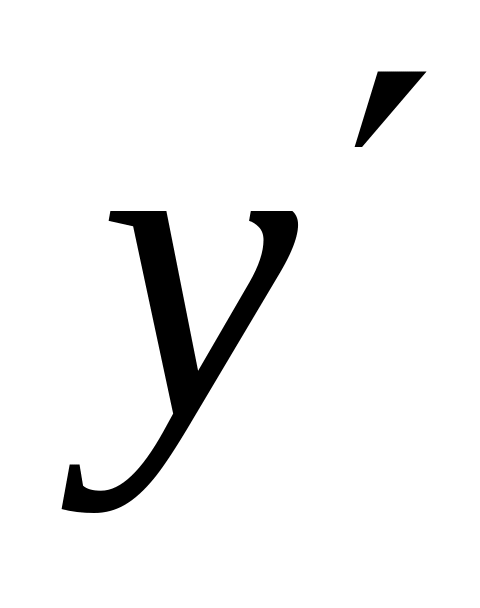 не существует, нет.
не существует, нет.Исследуем критические точки по достаточному признаку экстремума. Это удобно делать в таблице, куда заносятся критические точки и точки разрыва функции (в данном примере точек разрыва нет).
-
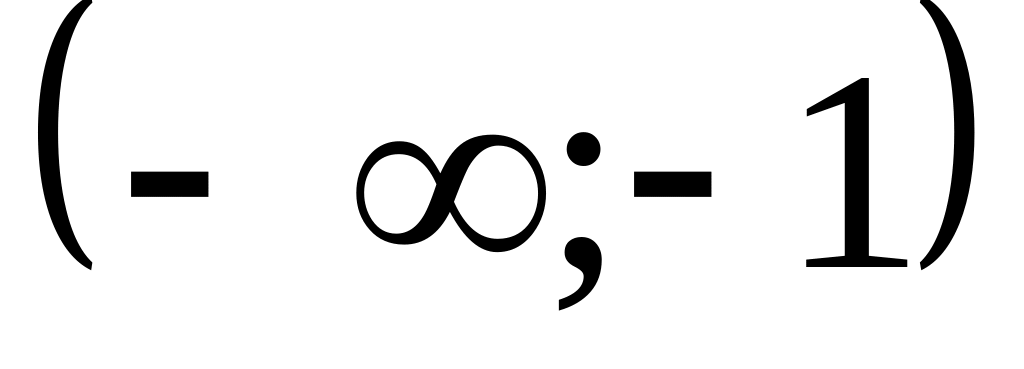

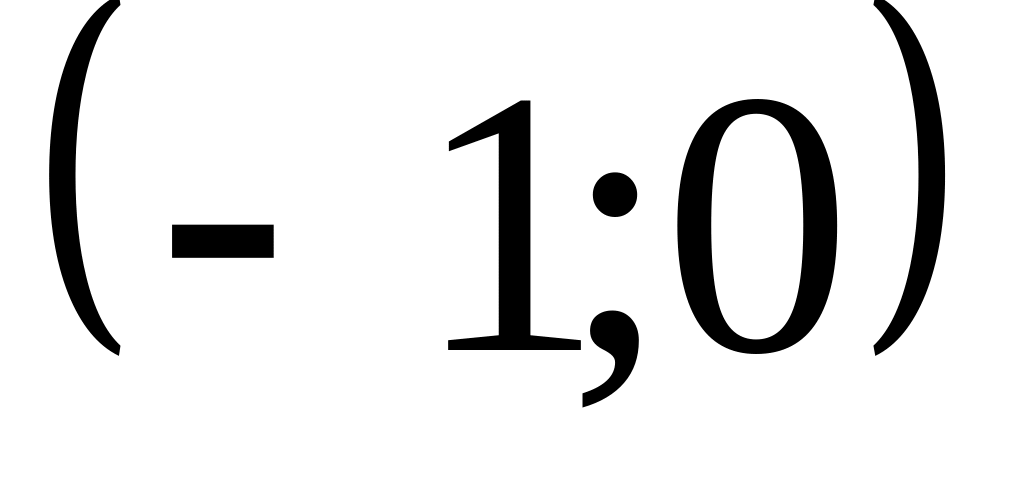
0

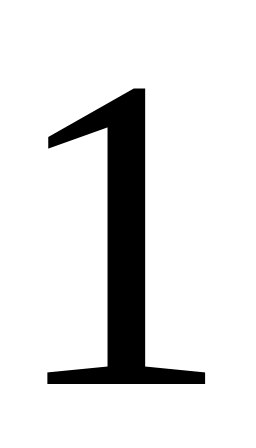
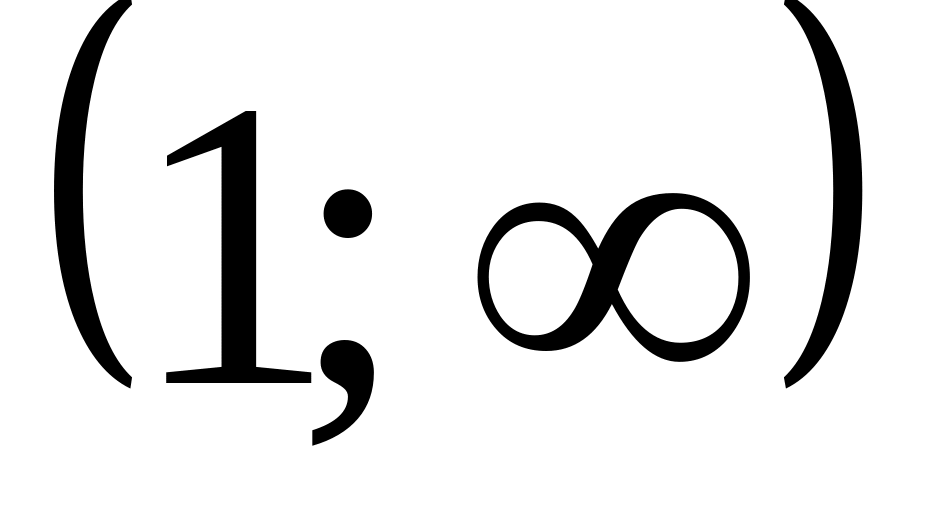
0
0
0
нет экстремума
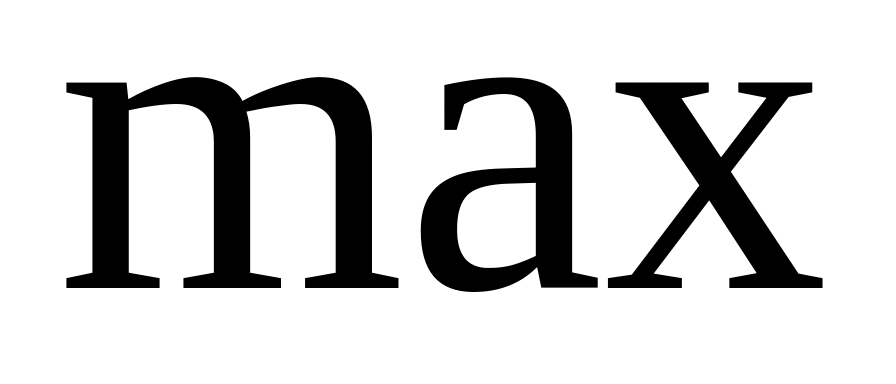
нет экстремума
Для нахождения знака
производной достаточно подставить в
нее любое значение из рассматриваемого
интервала. Так, исследуя интервал
![]() ,
можно взять, например, точку
,
можно взять, например, точку
![]() и подставить это значение в производную:
и подставить это значение в производную:
![]() .
Исследовав, указанным образом знаки
производной в интервалах
.
Исследовав, указанным образом знаки
производной в интервалах
![]() ,
замечаем, что производная меняет знак
при переходе через точку 0 (с “+” на
“”).
Значит,
,
замечаем, что производная меняет знак
при переходе через точку 0 (с “+” на
“”).
Значит,
![]() – точка максимума. Значение функции в
этой точке
– точка максимума. Значение функции в
этой точке
![]() .
.
Заметим, что, исследуя функцию на экстремум, мы одновременно находим и интервалы монотонности функции.
