
- •Кафедра высшей и прикладной математики
- •1.1. Предел последовательности
- •1.2. Предел функции
- •Геометрическая интерпретация. Пусть дан график функции , имеющей предел при , равный (рис.2).
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов
- •1.3. Раскрытие неопределенностей
- •1.4. Первый замечательный предел
- •1.5. Второй замечательный предел
- •2.1. Понятие производной функции
- •Формулы дифференцирования
- •2.2. Производная сложной функции
- •Пример. Найти производную функции .
- •2.3. Дифференцирование неявной функции
- •Признаки возрастания и убывания функции
- •3.1. Экстремум функции
- •3.2. Точки перегиба График функции называется выпуклым на интервале , если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
- •На интервале кривая выпукла , а на интервале – вогнута . Таким образом, при переходе через точку вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты .
- •3.3. Асимптоты
- •3.4. Общая схема исследования функции и построение ее графика
- •4.1. Первообразная функция и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •4.2. Непосредственное интегрирование
- •4.3. Интегрирование методом замены переменной (метод подстановки)
- •4.4. Интегрирование по частям
- •4.5. Интегрирование рациональных дробей
- •4.6. Интегрирование тригонометрических функций
- •5.1. Понятие определенного интеграла
- •Основные свойства определенного интеграла
- •5.2. Формула Ньютона-Лейбница
- •5.3. Методы интегрирования
- •7.1. Уравнение с разделяющимися переменными
- •7.2. Однородные дифференциальные уравнения первого порядка
- •7.3. Линейные дифференциальные уравнения
- •7.4. Дифференциальные уравнения второго порядка
- •7.5. Дифференциальные уравнения второго порядка с постоянными коэффициентами
- •8.1. Необходимый признак сходимости числового ряда
- •8.2. Достаточные признаки сходимости знакоположительных рядов
- •8.3. Знакочередующиеся ряды
- •Обобщенный признак Даламбера сходимости степенного ряда Для степенного ряда , где , составим предел модуля отношения последующего члена ряда к предыдущему
- •ЛиТература
4.1. Первообразная функция и неопределенный интеграл
Основной задачей
дифференциального исчисления является
определение для заданной функции
![]() ее производной
ее производной
![]() или ее дифференциала
или ее дифференциала
![]() .
.
Обратная задача,
состоящая в определении функции
по ее известным производной
или дифференциалу
![]() ,
представляет собой основную задачу
интегрального исчисления.
,
представляет собой основную задачу
интегрального исчисления.
Определение. |
Первообразной функцией функции , определенной на некотором промежутке, называется функция , существующая на том же промежутке и удовлетворяющая условию
или
|
Процесс нахождения первообразной функции для заданной функции называется ее интегрированием.
Если
функция
является первообразной для функции
,
то и функция
![]() ,
где
,
где
![]() – производная постоянная величина,
также является первообразной функции
.
Таким образом, если функция
имеет первообразную, то она имеет их
бесчисленное множество, причем все они
отличаются одна от другой только
постоянным слагаемым.
– производная постоянная величина,
также является первообразной функции
.
Таким образом, если функция
имеет первообразную, то она имеет их
бесчисленное множество, причем все они
отличаются одна от другой только
постоянным слагаемым.
Определение. |
Неопределенным интегралом от функции называется совокупность всех ее первообразных и обозначается:
|
Здесь
![]() знак интеграла,
– подынтегральная функция,
знак интеграла,
– подынтегральная функция,
![]() – подынтегральное выражение,
– переменная интегрирования,
– произвольная постоянная величина.
– подынтегральное выражение,
– переменная интегрирования,
– произвольная постоянная величина.
Основные свойства неопределенного интеграла
1о |
Постоянный множитель можно выносить за знак интеграла
|
2о |
Неопределенный интеграл от дифференциала функции равен сумме этой функции и произвольной постоянной
|
3о |
Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению
а)
|
4о |
Неопределенный интеграл от алгебраической суммы конечного числа функций равен такой же алгебраической сумме неопределенных интегралов от слагаемых функций
|
Таблица основных интегралов
К основным методам интегрирования относятся: непосредственное интегрирование, метод замены переменной и интегрирование по частям.
4.2. Непосредственное интегрирование
Непосредственное интегрирование производится путем применения свойств интеграла, соответствующего табличного интеграла и формул
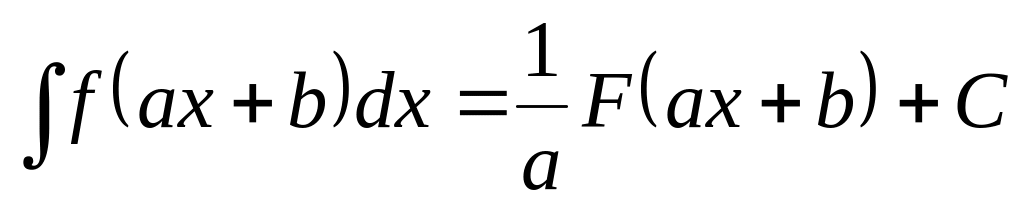 ;
; ;
;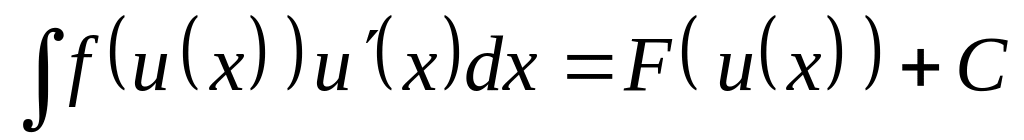 .
.
Пример.
Найти интеграл
![]() .
.
Решение.
![]() .
.
Пример.
Найти интеграл
![]() .
.
Решение.
![]() .
.
Пример.
Найти интеграл
![]() .
.
Решение.
![]()
