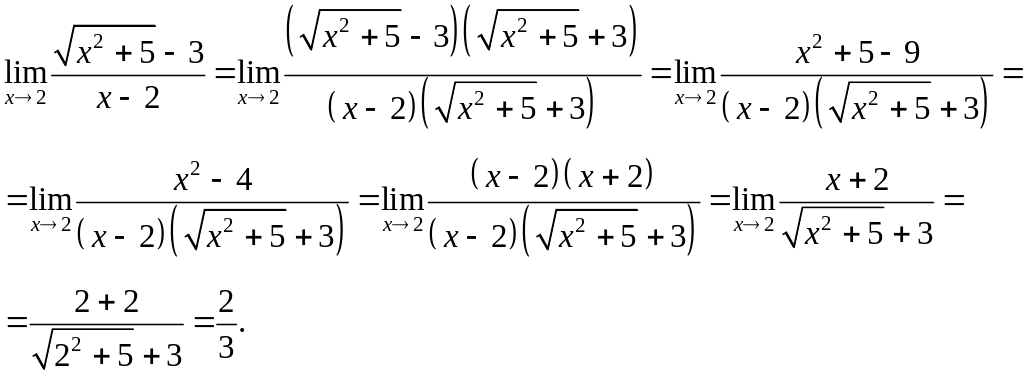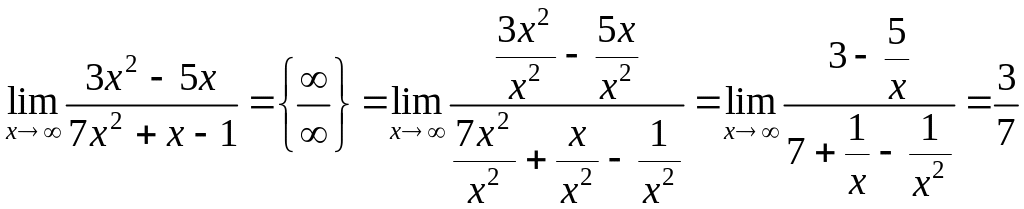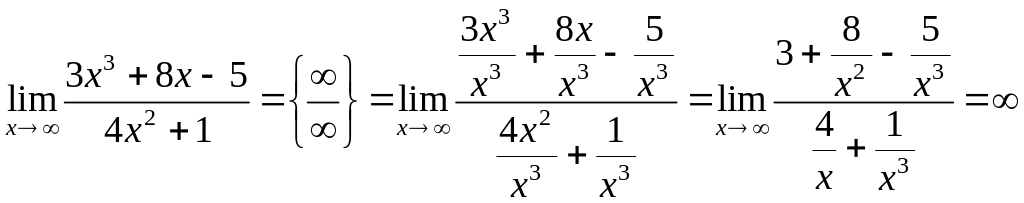Бесконечно малые и бесконечно большие функции

Функция называется бесконечно малой при , если

.

Функция называется бесконечно большой при , если для всех значений из некоторой окрестности точки выполняется неравенство , где – любое положительное число, даже сколь угодно большое. В этом случае пишут:

.

Функция называется ограниченной при , если существует такое положительное число , что для всех значений из окрестности числа выполняется неравенство .

Связь между бесконечно большими и

бесконечно малыми функциями:

• Если при – бесконечно большая функция, то функция 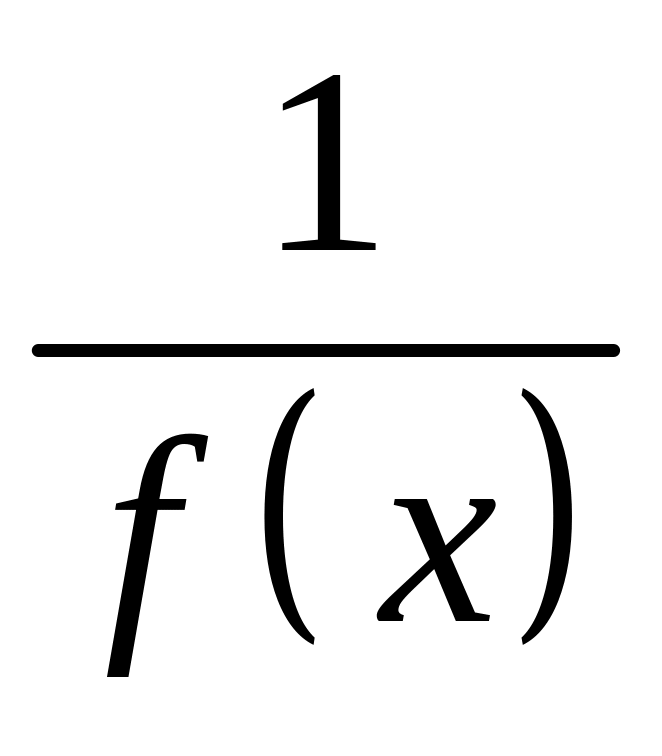бесконечно малая (условно: ).

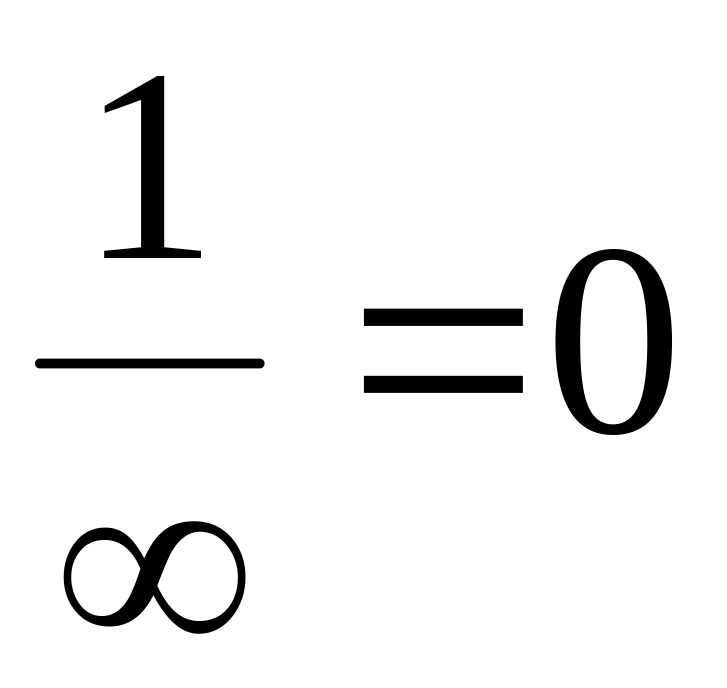• Если при функция 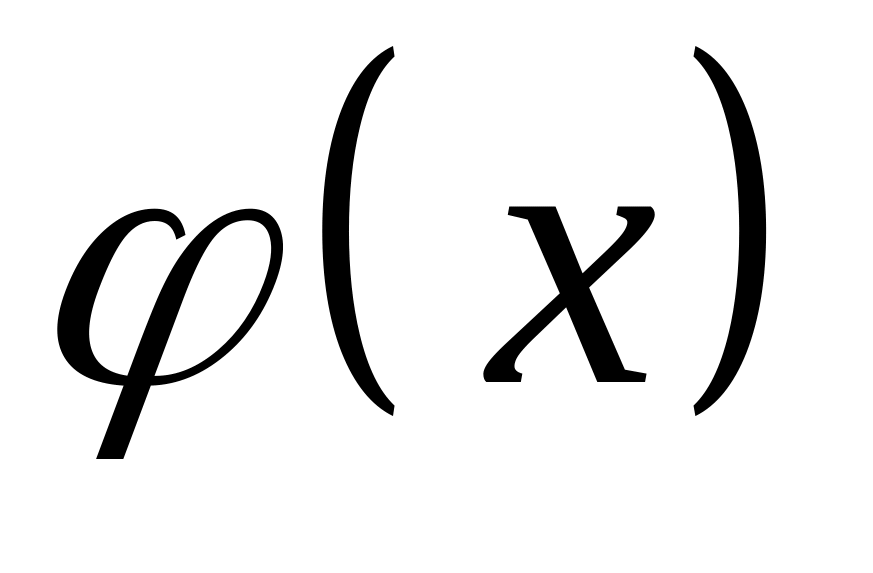бесконечно малая, то функция 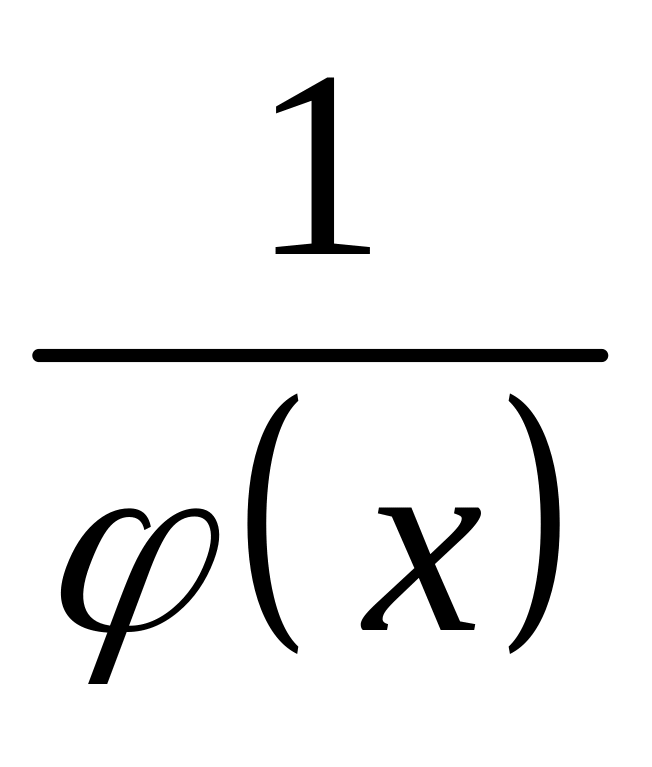– бесконечно большая, причем предполагается, что в окрестности точки функция в нуль не обращается (условно : ).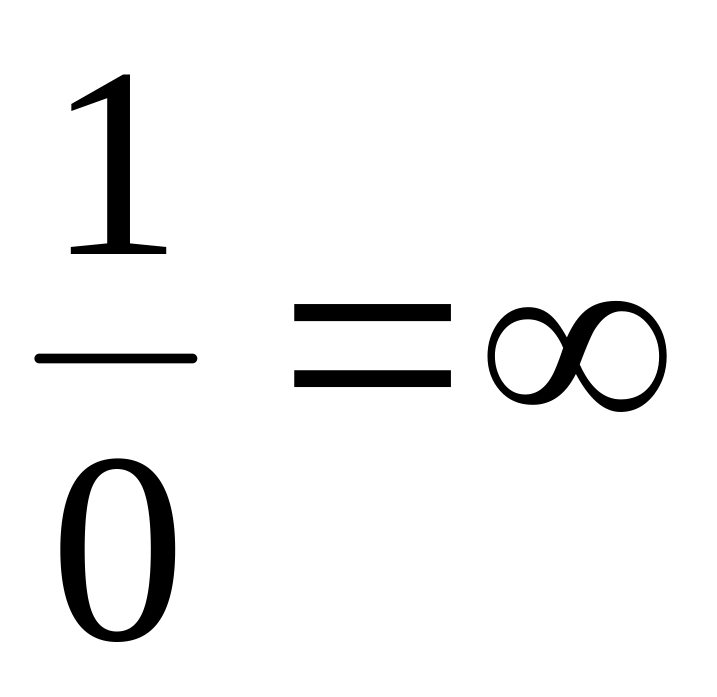

Свойства пределов

Пусть функции имеют пределы при . Тогда

1. Предел постоянной равен самой этой постоянной

.

2. Постоянный множитель можно выносить за знак предела

.

3. Предел алгебраической суммы конечного числа функций равен сумме пределов функций, если эти пределы существуют

.

4. Предел произведения конечного числа функций равен произведению пределов этих функций, если эти пределы существуют

.

5. Предел частного двух функций равен частному их пределов, если

.

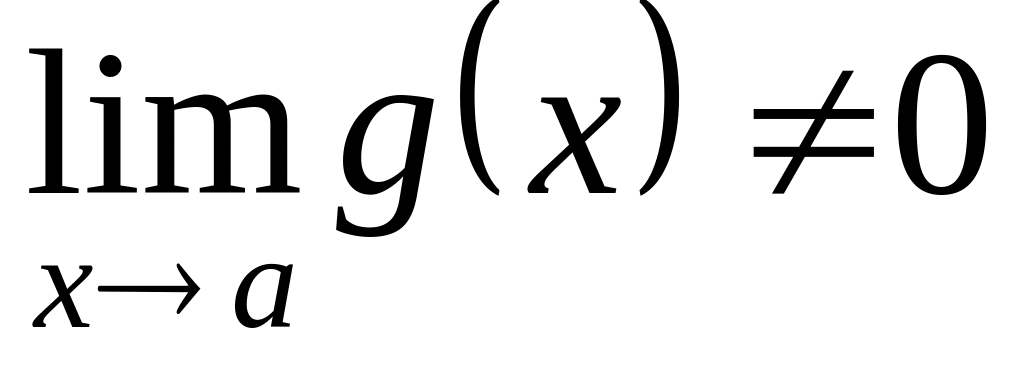
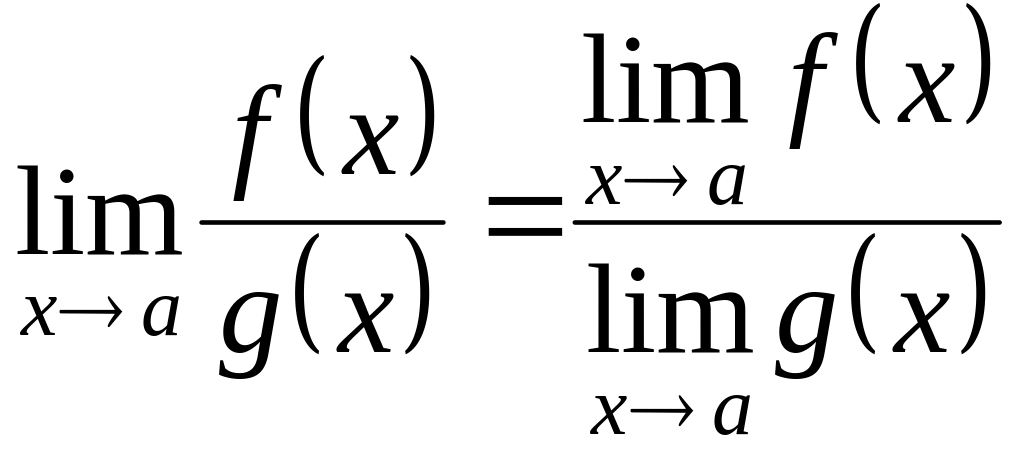6. Предел степени равен пределу основания в степени предела показателя степени

.

7. Предел логарифма равен логарифму предела

.

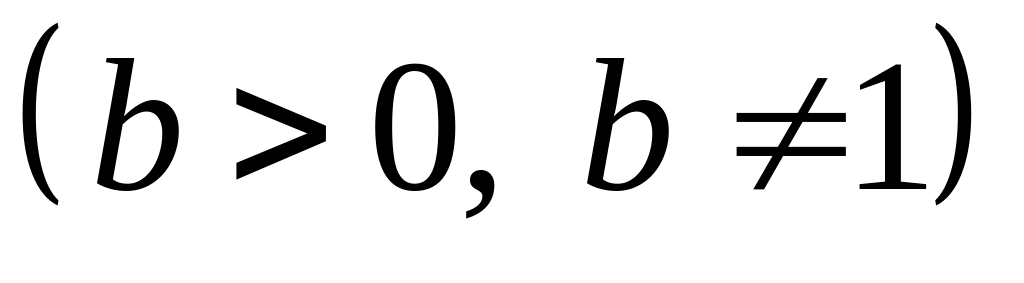
1.3. Раскрытие неопределенностей

При нахождении предела функции нужно в выражении функции заменить аргумент его предельным значением. Если при этом не возникает трудностей (неопределенностей различных видов), то предел вычисляется легко. Например

.

Однако, не всегда удается простой подстановкой вычислить предел. Рассмотрим некоторые приемы отыскания пределов в случае неопределенностей.

Неопределенность вида , порожденную отношением многочленов, раскрывают делением числителя и знаменателя на аргумент в наибольшей степени дроби.

Пример. Найти

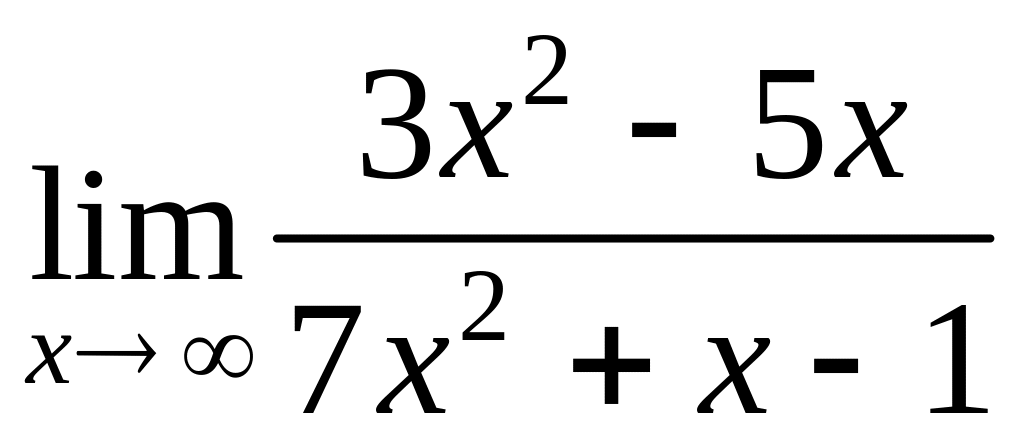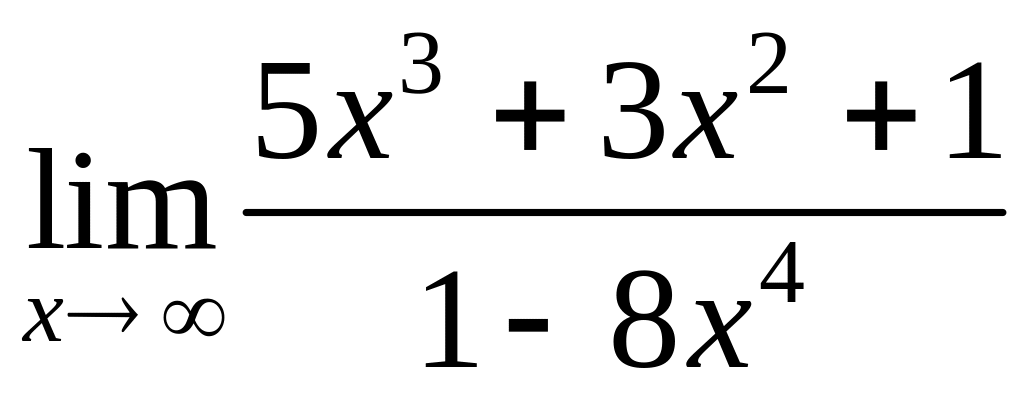1. . 2) . 3) .

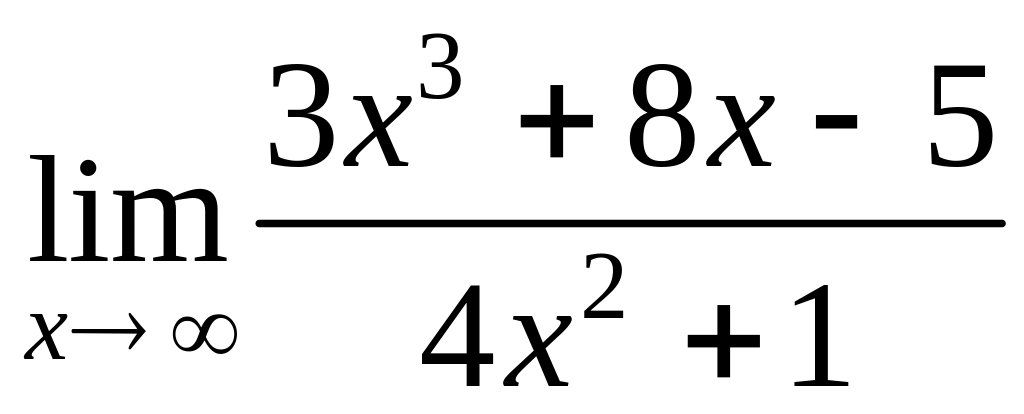Решение.

При и числитель, и знаменатель дроби бесконечно большие. Значит имеем дело с отношением двух бесконечно больших функций. Для решения задачи следует разделить числитель и знаменатель на в высшей степени (в данном случае на ), а после перейти к непосредственному вычислению предела. Итак

1. 

(величины при являются бесконечно малыми величинами, поэтому ).

В данном примере степень числителя равна степени знаменателя.

2. 

В данном примере степень числителя меньше степени знаменателя.

3. 

В данном примере степень числителя больше степени знаменателя.

Правило раскрытия неопределенности вида

1. если степень числителя больше степени знаменателя, то предел равен ;

2. если степень числителя равна степени знаменателя, то предел равен отношению коэффициентов при старших степенях в числителе и знаменателе;

3. если степень числителя меньше степени знаменателя, то предел равен 0.

Неопределенность вида , порожденную разностью двух бесконечно больших величин одного знака, раскрывают домножением на сопряженное выражение, приведением к общему знаменателю или вынесением общего множителя. При домножении на сопряженное выражение следует одновременно разделить на него.

Пример. Найти

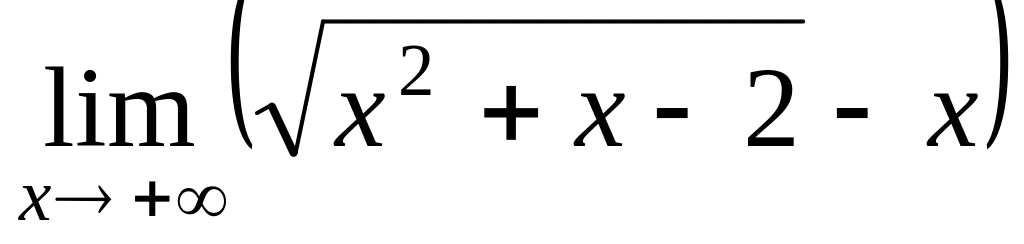1. . 2)

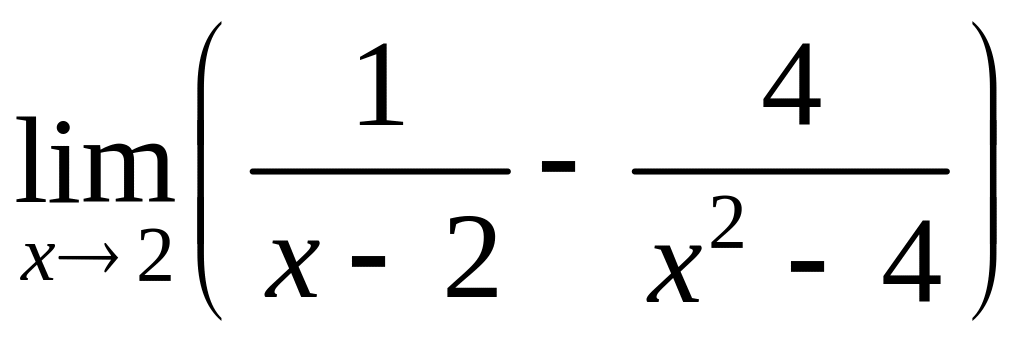
Решение.

1. Умножим и разделим выражение, стоящее под знаком предела, на сопряженное:

.

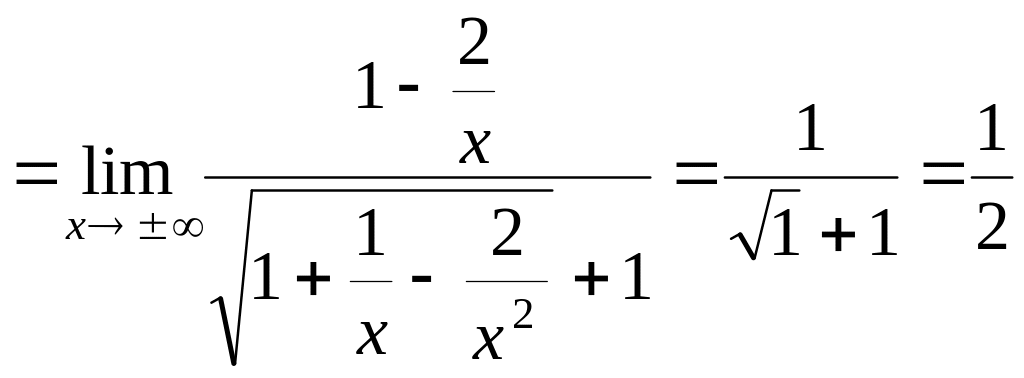2. Приводим к общему знаменателю и преобразуем

.

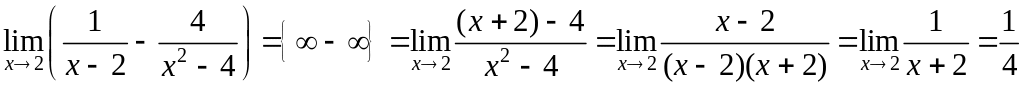Неопределенность вида при , порожденную отношением двух многочленов, раскрывают выделением в числителе и знаменателе множителя и сокращением на него.

Для раскрытия неопределенности , содержащей иррациональные выражения, следует числитель и знаменатель домножить на сопряженное выражение для иррационального, после чего сделать необходимые упрощения и вычислить предел.

Пример. Найти

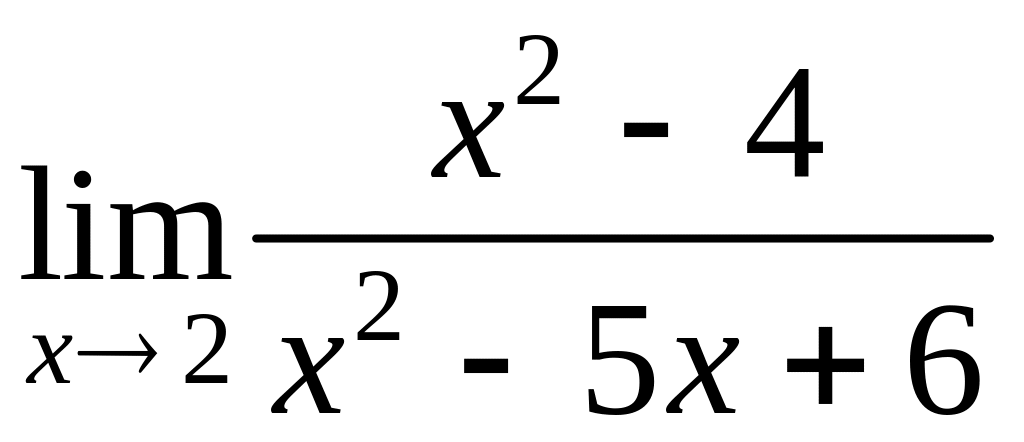1. . 2) .

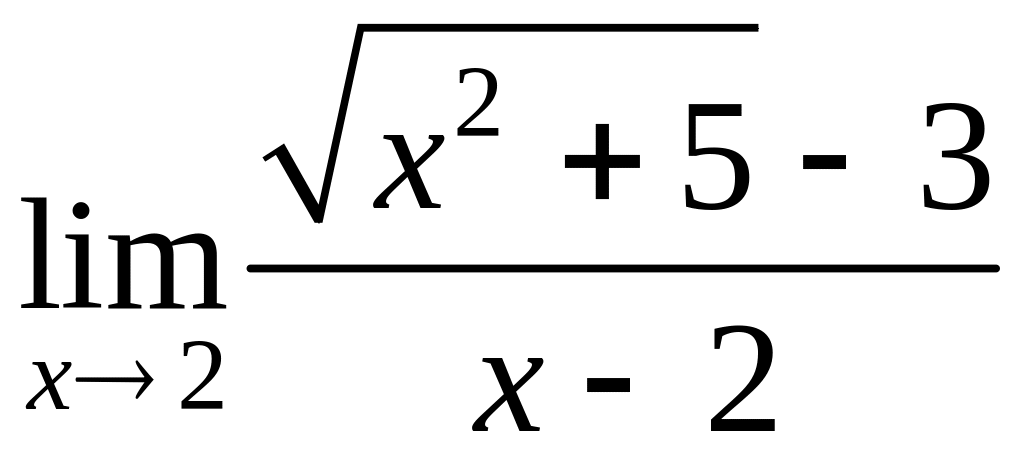Решение.

1. Разложим числитель и знаменатель на множители:

.

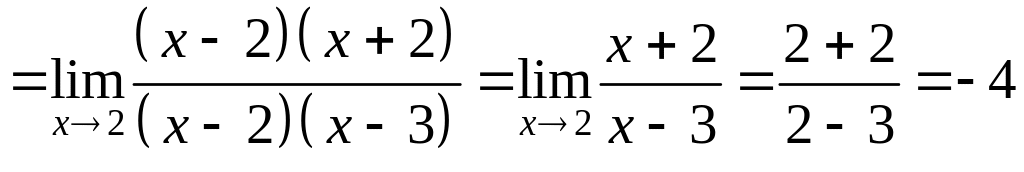2. Перенесем иррациональность в знаменатель, для чего умножим числитель и знаменатель на выражение, сопряженное числителю, ( 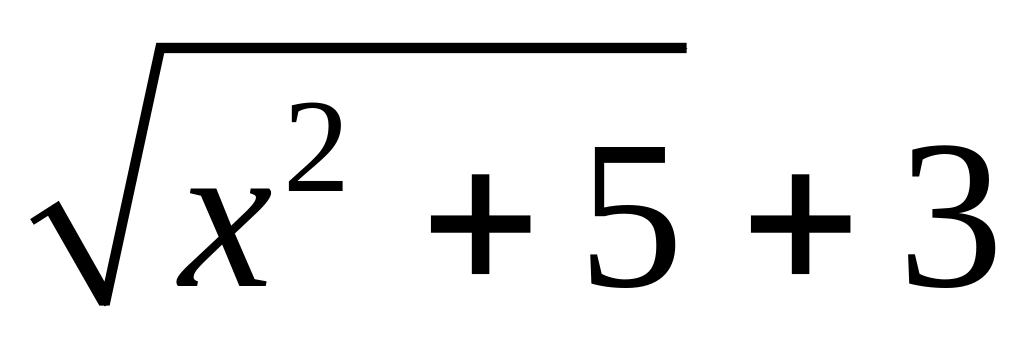) и получим: