7.1. Уравнение с разделяющимися переменными
Этот тип уравнения является самым простым типом уравнений первого порядка.
Дифференциальное уравнение вида
называется уравнением с разделяющимися переменными.
Представим производную
как отношение дифференциалов
,
тогда
.
Умножаем на
.
Разделение переменных
производится делением обеих частей
последнего соотношения на произведение
,
в котором
,
.
После деления уравнение примет вид
или
,
а его общий интеграл запишется так:
или
.
Пример.
Решить уравнение
.
Решение. Подставим вместо
.
.
Разделим на
.
Интегрируя, получим
.
Здесь удобно представить константу в логарифмической форме. Из последнего равенства получим
или окончательно
.
7.2. Однородные дифференциальные уравнения первого порядка
Функция
называется однородной степени
,
если для нее выполняется равенство
.
Однородными функция будут:
– вторая степень
однородности
– вторая степень
однородности
– первая степень
однородности
– нулевая степень
однородности
Неоднородные
функции:
,
,
.
Однородным дифференциальным уравнением первого порядка называют соотношение вида
,
где
и
– однородные функции одинаковой степени
однородности.
Дифференциальное уравнение может быть представлено в виде
.
Для решения однородных дифференциальных уравнений первого порядка применяют подстановку
,
где – новая искомая функция, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
После того как новое
уравнение будет проинтегрировано,
следует
заменить на
.
Пример.
Решить уравнение
.
Решение.
Убедимся, что это уравнение однородное.
Заменить
на
,
а
на
,
видим, что уравнение не изменилось это
и доказывает, что оно однородное.
Сделаем подстановку:
,
откуда
,
и уравнение перепишется так:
,
,
,
.
Теперь мы получили уравнение с разделяющимися переменными, которое после разделения переменных запишется следующим образом:
.
Интегрируя, получаем:
,
или
.
Заменяя на , получим
;
;
.
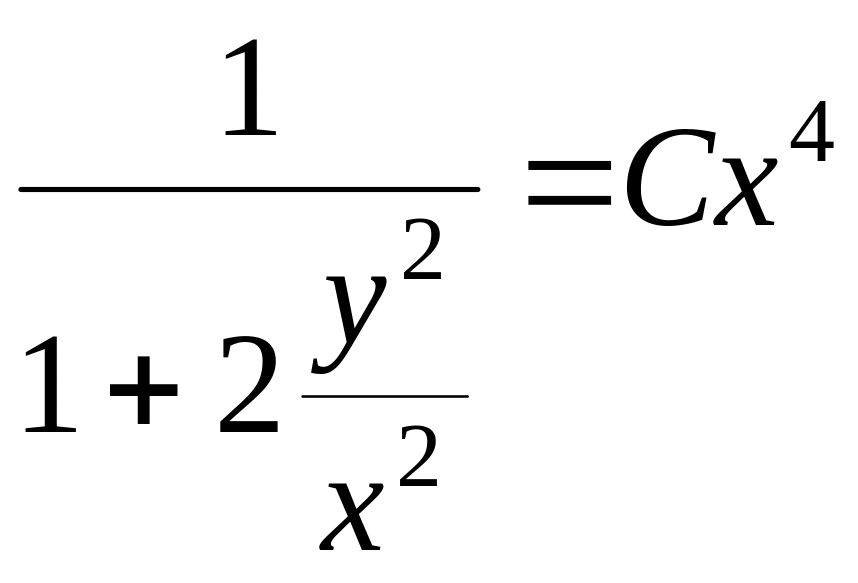7.3. Линейные дифференциальные уравнения
первого порядка
Дифференциальные уравнения вида
называются линейными потому, что искомая функция и ее производная входят в уравнение в первой степени.
Функции
и
предполагаются непрерывными в промежутке
,
в котором ищется решение уравнения.
Линейное дифференциальное
уравнение первого порядка при помощи
подстановки
сводится к двум уравнениям с разделяющимися
переменными.
Пример.
Решить уравнение
.
Решение.
Запишем уравнение в виде:
.
Разделяя на
,
получим:
.
Полагаем
,
тогда
и данное уравнение примет вид:
,
или
.
Решаем уравнение
,
находим его простейшее решение
,
откуда
;
.
Подставляя в уравнение , получим уравнение
,
откуда
,
,
,
.
Значит, искомое общее решение можно записать в виде:
.
7.4. Дифференциальные уравнения второго порядка
Дифференциальным уравнение второго порядка называется соотношение вида
.
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные
.
Наиболее простыми из дифференциальных уравнений второго порядка являются уравнения, разрешенные относительно второй производной и имеющие вид
.
Их решение находят двукратным интегрированием:
,
.
Пример.
Решить уравнение
.
Решение. Находим
,
.