
- •Кафедра высшей и прикладной математики
- •1.1. Предел последовательности
- •1.2. Предел функции
- •Геометрическая интерпретация. Пусть дан график функции , имеющей предел при , равный (рис.2).
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов
- •1.3. Раскрытие неопределенностей
- •1.4. Первый замечательный предел
- •1.5. Второй замечательный предел
- •2.1. Понятие производной функции
- •Формулы дифференцирования
- •2.2. Производная сложной функции
- •Пример. Найти производную функции .
- •2.3. Дифференцирование неявной функции
- •Признаки возрастания и убывания функции
- •3.1. Экстремум функции
- •3.2. Точки перегиба График функции называется выпуклым на интервале , если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
- •На интервале кривая выпукла , а на интервале – вогнута . Таким образом, при переходе через точку вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты .
- •3.3. Асимптоты
- •3.4. Общая схема исследования функции и построение ее графика
- •4.1. Первообразная функция и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •4.2. Непосредственное интегрирование
- •4.3. Интегрирование методом замены переменной (метод подстановки)
- •4.4. Интегрирование по частям
- •4.5. Интегрирование рациональных дробей
- •4.6. Интегрирование тригонометрических функций
- •5.1. Понятие определенного интеграла
- •Основные свойства определенного интеграла
- •5.2. Формула Ньютона-Лейбница
- •5.3. Методы интегрирования
- •7.1. Уравнение с разделяющимися переменными
- •7.2. Однородные дифференциальные уравнения первого порядка
- •7.3. Линейные дифференциальные уравнения
- •7.4. Дифференциальные уравнения второго порядка
- •7.5. Дифференциальные уравнения второго порядка с постоянными коэффициентами
- •8.1. Необходимый признак сходимости числового ряда
- •8.2. Достаточные признаки сходимости знакоположительных рядов
- •8.3. Знакочередующиеся ряды
- •Обобщенный признак Даламбера сходимости степенного ряда Для степенного ряда , где , составим предел модуля отношения последующего члена ряда к предыдущему
- •ЛиТература
3.2. Точки перегиба График функции называется выпуклым на интервале , если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
График функции называется вогнутым на интервале , если он расположен выше касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 б).

Рис. 8 а Рис. 8 б
ТЕОРЕМА |
(достаточный признак выпуклости (вогнутости) графика функции)
Если
|
Точка кривой, отделяющая ее выпуклую дугу от вогнутой, называется точкой перегиба.
Точки кривой, в которых
вторая производная
![]() или не существует, называются критическими
точками второго рода. Точки перегиба
следует искать среди критических точек
второго рода.
или не существует, называются критическими
точками второго рода. Точки перегиба
следует искать среди критических точек
второго рода.
В критической точке
второго рода
![]() перегиб будет только в том случае, когда
при переходе через эту точку
перегиб будет только в том случае, когда
при переходе через эту точку
![]() меняет знак.
меняет знак.
Правило. Для определения точек перегиба кривой надо определить все критические точки второго рода и рассмотреть знаки в каждых двух соседних интервалах, на которые эти точки делят область определения функции. В случае, если знаки в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
Пример.
Определить интервалы выпуклости и
вогнутости, точки перегиба графика
функции
![]() .
.
Решение.
Область определения функции – интервал
![]() .
.
Найдем первую и вторую производные функции
![]() ,
,
![]() .
.
Так как
![]() при любом значении
,
то кривая вогнута на всем интервале
.
Точек перегиба нет.
при любом значении
,
то кривая вогнута на всем интервале
.
Точек перегиба нет.
Пример.
Определить интервалы выпуклости и
вогнутости и точки перегиба графика
функции
![]() .
.
Решение. Область определения функции – интервал .
Найдем первую и вторую производные функции
![]() ,
,
![]() .
.
Решаем уравнение
![]() и находим, что
и находим, что
![]() .
Это единственная критическая точка.
Она делит область определения функции
на два интервала
.
Это единственная критическая точка.
Она делит область определения функции
на два интервала
![]() и
и
![]() .
.

– +
0
На интервале кривая выпукла , а на интервале – вогнута . Таким образом, при переходе через точку вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты .
3.3. Асимптоты
Определение. |
Если расстояние от
кривой
|
Различают асимптоты: вертикальные и наклонные.
Кривая имеет вертикальную асимптоту
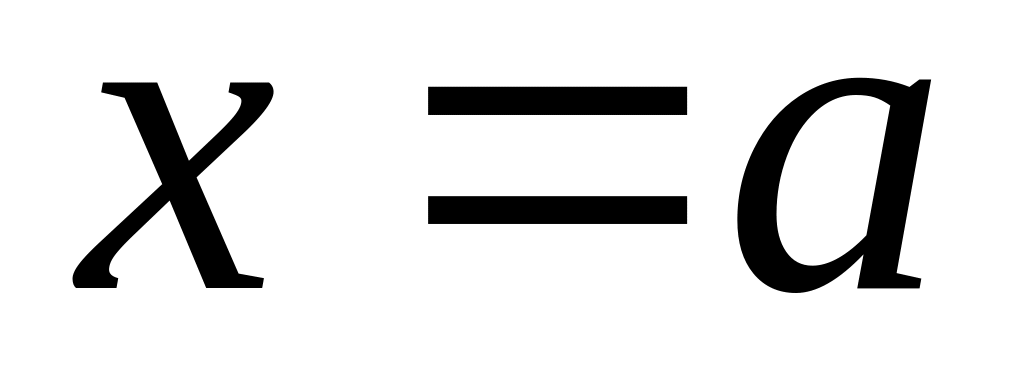 ,
если при
,
,
если при
,
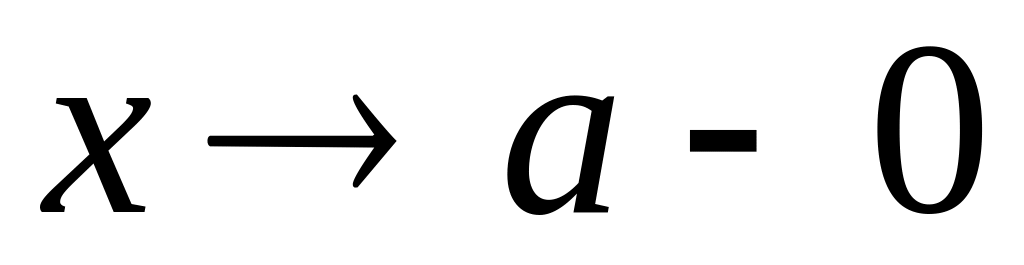 или при
или при
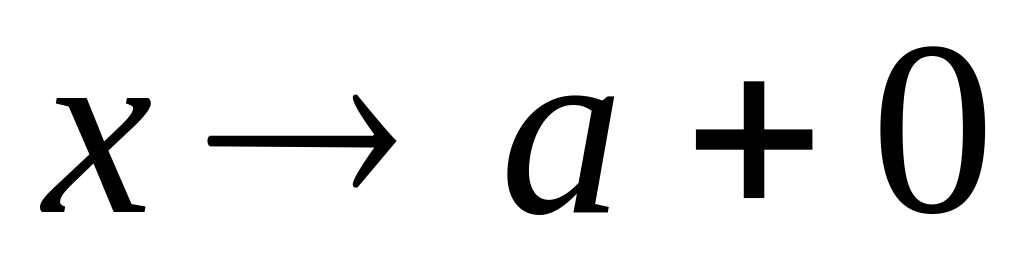
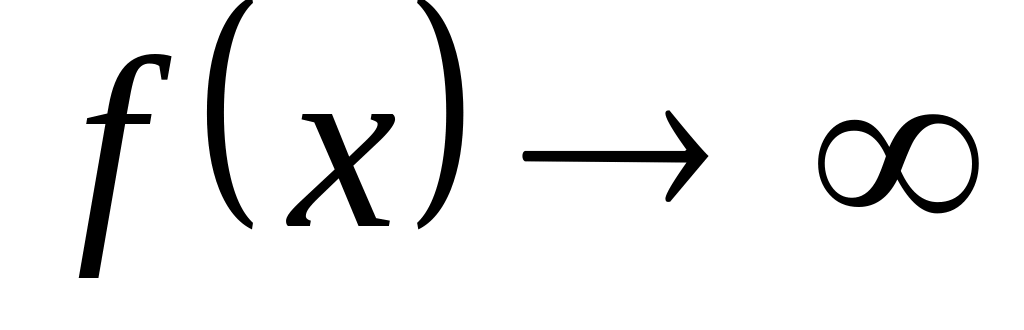 .
Для определения вертикальных асимптот
надо отыскать те значения аргумента,
вблизи которых
неограниченно возрастает по абсолютной
величине. Если такими значениями
аргумента являются
.
Для определения вертикальных асимптот
надо отыскать те значения аргумента,
вблизи которых
неограниченно возрастает по абсолютной
величине. Если такими значениями
аргумента являются
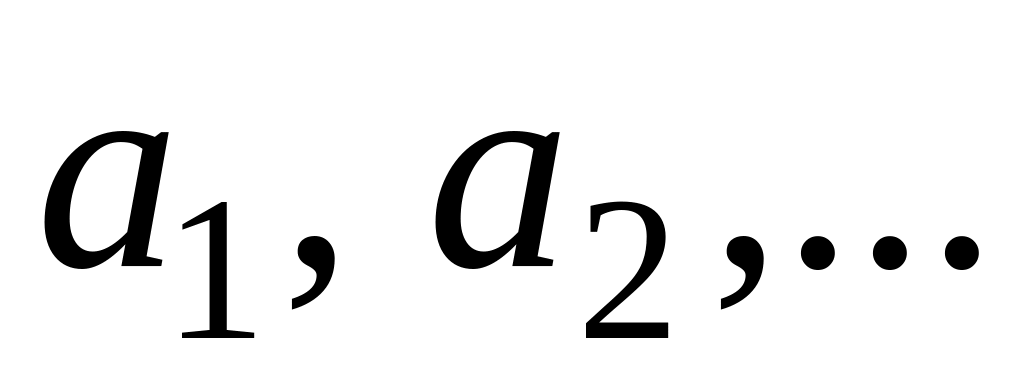 ,
то уравнения вертикальных асимптот
будут
,
то уравнения вертикальных асимптот
будут
![]() ;
;
![]() ;
…
;
…
Вертикальные асимптоты
– это нули знаменателя функции. Например,
![]() .
Здесь две вертикальные асимптоты:
.
Здесь две вертикальные асимптоты:
![]() ,
,
![]()
Для определения наклонной асимптоты
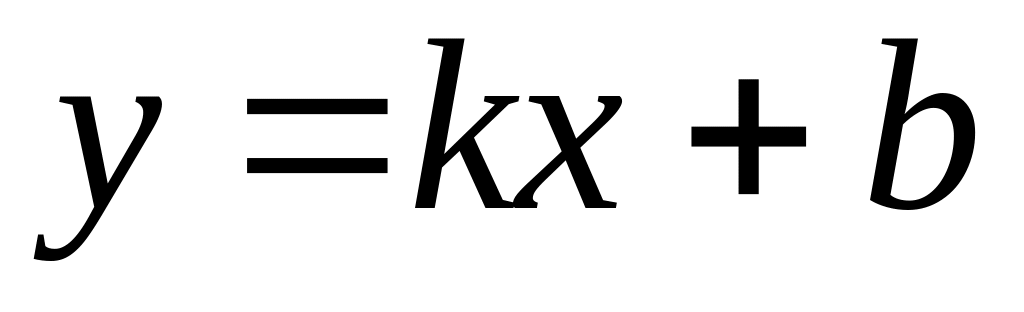 кривой
надо найти числа
кривой
надо найти числа
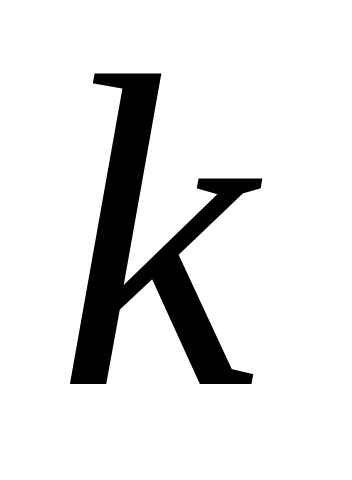 и
и
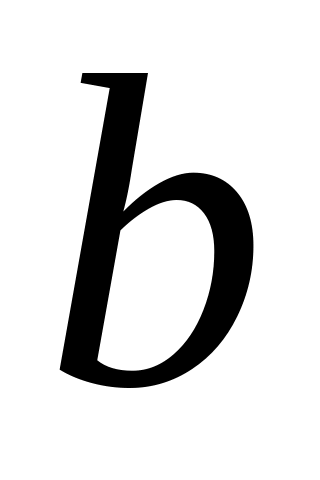 по формулам
по формулам
![]() ,
,
![]()
(иногда следует
отдельно рассматривать случаи
![]() и
и
![]() ).
).
