Операторы кинетической энергии, момента импульса, функции Гамильтона, энергии в координатном представлении.

На основе принципа соответствия по известному явному виду операторов канонических переменных (координат и проекций вектора импульса) легко записать явный вид оператора любой физической величины в том же представлении. Для этого в классическую формулу физической величины вместо координат и проекций импульсов следует вставить соответствующие операторы. Важно при этом проверить эрмитовость полученного оператора.

Так классическая формула для кинетической энергии 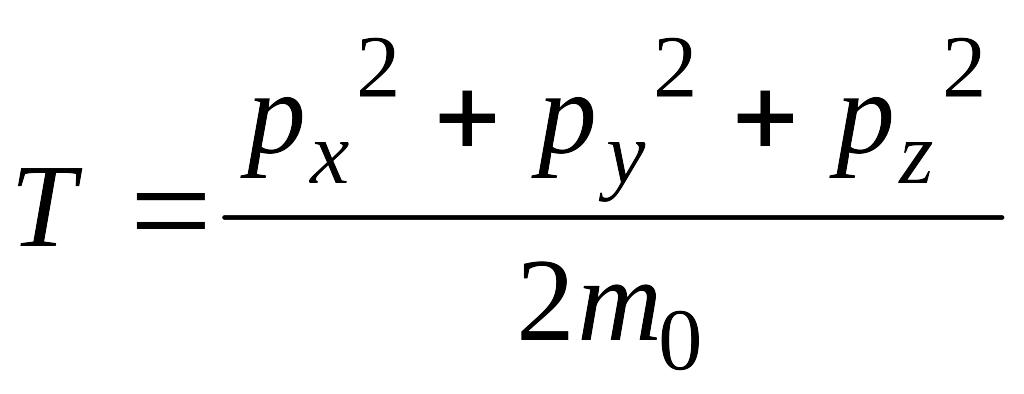, где - масса частицы, позволяет записать оператор кинетической энергии в виде:

. (6.24)

Легко видеть, что если - эрмитовые операторы, то и квадраты их, а затем и сумма последних есть эрмитов оператор.

По классической формуле для механического момента импульса движущейся частицы

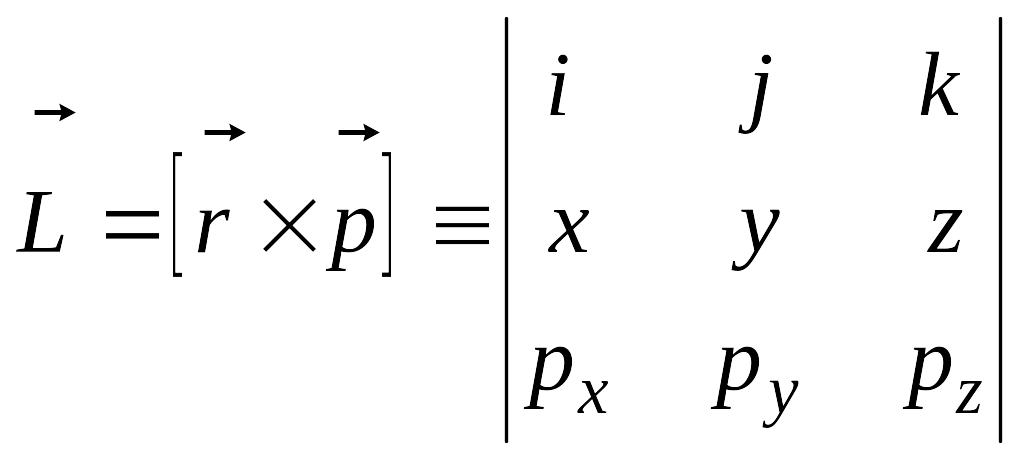
легко записать операторы проекций и квадрата механического момента:

(6.25)

Не составляет труда проверить линейность и эрмитовость этих операторов.

В теоретической физике большое значение имеет функция Гамильтона: . Оператор ее называется гамильтонианом квантовой системы. Если учесть, что время в квантовой механике считается параметром, то гамильтониан частицы, движущейся в переменном потенциальном поле, имеет вид:

. (6.26)

В случае стационарных потенциальных полей, когда , функция Гамильтона , равная сумме кинетической и потенциальной энергии, представляет полную энергию , поэтому гамильтониан в этом случае является оператором энергии:

. (6.27)

Уравнение для собственных функций и собственных значений оператора в этом случае называется стационарным уравнением Шредингера или уравнением для стационарных состояний

. (6.28)

6.3. Средние значения физических величин в координатном представлении

В состоянии  квантовой системы среднее значение физических величин определяется по формуле (5.10) или по формуле (5.12), если норма вектора  не равна 1.

Ограничиваясь рассмотрением одномерного случая, примем во внимание, что состояние квантовой системы описывается волновой функцией и явный вид операторов координаты и импульса в координатном представлении имеют вид:

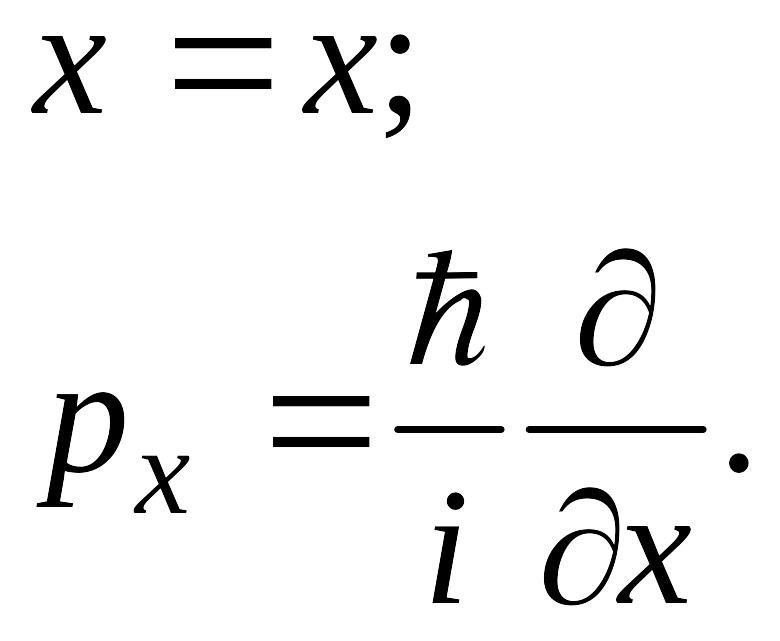
Тогда средние значения координаты и импульса представятся выражениями:

(6.29)

. (6.30)

§7. Импульсное представление

Согласно постулатам квантовой механики любая физическая величина изображается самосопряженным линейным оператором. Явный вид оператора зависит от выбранного представления. Так в координатном представлении операторы координат и проекций импульса определены формулами (6.13) и (6.23). Знание этих операторов позволяет с помощью принципа соответствия записать операторы других физических величин в этом же представлении.

7.1. Векторы состояния и операторы физических величин в импульсном представлении

И в импульсном представлении прежде всего надо найти явный вид операторов координат и проекций импульсов .

Рассмотрим ради простоты одномерный случай: движение частицы вдоль оси Ox, тогда импульс ее изображается оператором Найдем явный вид оператора в импульсном представлении. Для этого используем уравнение для собственных векторов и собственных значений оператора :

(7.1)

Пусть в результате действия оператора на некоторый вектор гильбертова пространства получается другой вектор :

. (7.2)

Воспользуемся Фурье-разложением векторов  и  по базисным векторам :

, (7.3)

где

. (7.4)

Тогда уравнение (7.2) приводится к виду:

. (7.5)

Подставляя (7.3) в уравнение (7.2), получим

, (7.6)

откуда с учетом (7.1) следует соотношение:

. (7.7)

Из сравнения (7.7) и (7.5) находим явный вид оператора в импульсном представлении:

. (7.8)

Аналогичным способом можно получить:

.

Таким образом, в импульсном представлении

. (7.9)

Для определения явного вида оператора в импульсном представлении используем уравнение для собственных векторов и собственных значений этого оператора ( ) в « -представлении». Для этого разложим вектор в интеграл Фурье по базисным векторам :

, (7.10)

где коэффициенты разложения , являясь собственными функциями оператора в импульсном представлении, вычисляются по формулам:

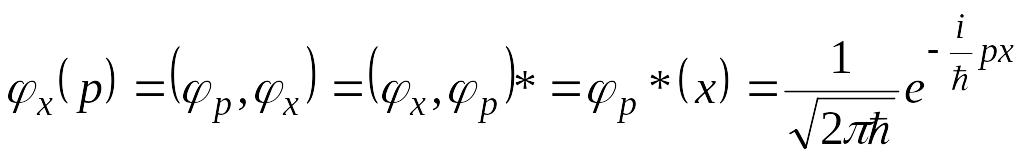(7.11)

(в преобразованиях учтены свойства скалярных произведений векторов унитарного пространства и формула (6.17)).

Уравнение для собственных функций и собственных значений оператора в импульсном представлении примет вид:

. (7.12)

Если учесть выражение (7.11), то уравнение (7.12) выполняется для

. (7.13)

Рассмотрим обобщение полученного выражения оператора . Выбрав произвольный вектор , описывающий квантовое состояние частицы, разложим его по базисным векторам в координатном представлении, а затем по в импульсном представлении:

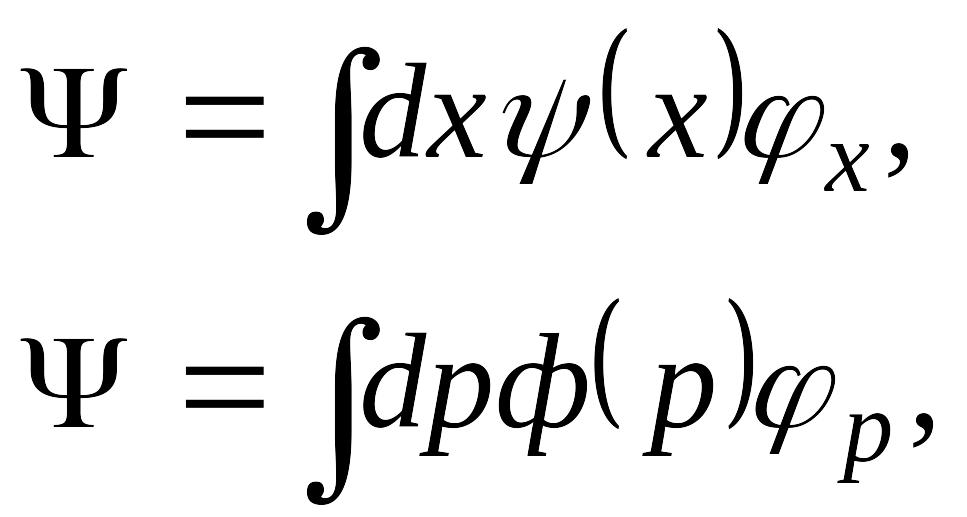
причем – совокупность коэффициентов разложения есть –вектор в импульсном представлении, называемый волновой функцией в p–представлении. Тогда, если справедлива формула (7.13), то должно выполняться уравнение

.

И действительно,

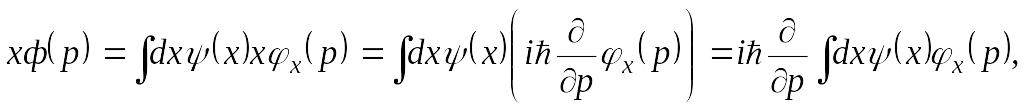
т.е.

откуда получаем:

. (7.14)

Итак, в импульсном представлении операторы координат имеют вид:

(7.15)

. (7.16)

7.2. Средние значения физических величин в импульсном представлении (одномерный случай p=p_x)

В состоянии  квантовой системы среднее значение физических величин определяется по формуле (5.10) или по формуле (5.12), если норма вектора  не равна 1.

Если волновая функция удовлетворяет условию нормировки

, (7.17)

то для расчета среднего значения физической величины справедлива формула

, (7.18)

в частности,

(7.19)

(7.20)