3. Методи і моделі управління товарними запасами у маркетингу

Задачею управління запасами називається оптимізаційна задача, у якій передбачаються відомими дані про поставки товару на склад, про попит на товар, про витрати і умови зберігання товарних запасів. Іншими словами, потрібно оптимізувати роботу складу за заданим критерієм оптимізації.

3.1. Класична задача управління запасами

Розглянемо цю задачу в класичній постановці. Виберемо за одиничний інтервал часу один день. Нехай до кінця дня на складі знаходиться запас в обсязі . Склад робить замовлення на поповнення запасу товару в об’ємі . Це поповнення надходить до початку наступного дня , так що запас товару на початку наступного дня становить . Нехай – об’єм товару, запитуваний споживачем (або споживачами) у день , тобто об’єм заявки.

Якщо , то склад задовольняє заявку споживача повністю, а залишки товару переносяться на наступний день , причому витрати зберігання цього запасу пропорційні його об’єму, тобто виконується відношення .

Якщо обсяг заявки , то склад повністю віддає свій запас, а за недопоставлений товар зазнає втрат (наприклад, штрафується за дефіцт), пропорційні обсягу дефіциту, тобто .

Отже, повні витрати складу можна записати у вигляді

. (3.1)

При цьому залишок товару становитиме .

З рівняння (3.1) треба: якщо , то ; якщо , то ; если , то .

У класичній постановці завдання керування запасами передбачається, що сама величина попиту невідома, однак вона є незалежною випадковою величиною, що має заданий закон розподілу. Нехай розподіл імовірностей величини задається безперервною функцією розподілу із щільністю розподілу . Тоді середні повні витрати задаються наступною формулою (тут – математичне сподівання)

.

Задача полягає у визначенні об’єму замовлення на поповнення , яке мінімізує середні повні витрати

. (3.2)

де . Позначимо , тоді у випадку статичної постановки класичної задачі управління запасами рівняння для визначення мінімізуючого запасу має вигляд

. (3.3)

Розв’язок (3.3) задачі (3.2) визначає стратегію оптимального поповнення запасів. Величина поповнення запасів , що мінімізує середні повні витрати, задається таким чином .

Конкретні числові характеристики системи керування запасами залежать від виду функції щільності розподілу випадкової величини попиту. У випадку симетричного «трикутного розподілу» попиту графік функції щільності розподілу має вигляд, представлений на рис.3.1.а, при цьому функція приймає наступний вид

(3.4)

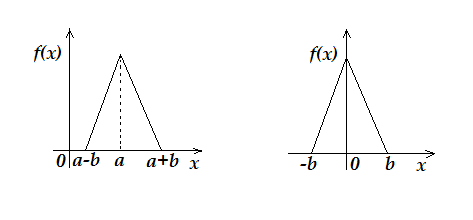
а) б)

Рисунок 3.1 – Графік функція щільності розподілу

Графік функції середніх повних витрат для такої функції попиту у випадку представлено на рис. 3.2, де оптимальний рівень запасу можна виразити формулою .

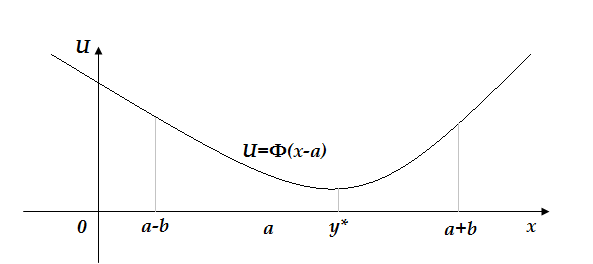
Рисунок 3.2 – Графік функції середніх повних витрат

У загальному виді для даної функції щільності розподілу попиту оптимальний рівень запасу задається умовами

(3.5)

Значення мінімуму середніх повних витрат має вигляд

(3.6)

З формул (3.5) і (3.6) випливає, що оптимальний рівень запасу при і мінімум середніх повних витрат при всіх і лінійно залежать від величини довжини інтервалу, на якому розкидані значення величини попиту на товар.

Приклад 3.1. Торгівельна фірма відповідно до договору реалізує зі складу за заявками холодильники, причому щоденний попит є випадковою величиною, функція щільності розподілу якої представлена графічно на рис. 3.1.а, і коливається від 20 до 80 холодильників у день. Середні витрати зберігання одного холодильника в день становлять 8 грн., а штраф за дефіцит (недопоставку) одного холодильника в день дорівнює 17 грн. Потрібно визначити стратегію оптимального поповнення запасу холодильників і мінімальні середні повні витрати.

Розв’язок: Запишемо математичні умови даного прикладу: (хол.), (хол.), (грн.), (грн.).

Відповідно до формули (3.5) оптимальний рівень запасу складає величину (хол.).

Тоді величина поповнення запасу холодильників, при якій середні повні витрати будуть мінімальними, задається наступними умовами

де – запас холодильників на складі фірми на кінець попереднього дня.

Так, якщо на кінець попереднього дня на складі фірми було 60 холодильників, то поповнювати запас не треба, а якщо на кінець попереднього дня на складі залишалося 25 холодильників, то варто реалізувати замовлення на поповнення запасу холодильників таким чином: .

Якщо дотримуватися цієї стратегії поповнення запасу, то мінімальний рівень середніх повних витрат, розраховуючи на один день, відповідно до формули (3.6) складе (грн.).