
- •МаркетингОві дослідження ринку
- •Передмова
- •1. Маркетинг як об'єкт застосуВання методів економіко-МатематиЧного моделювання
- •2. Балансові моделі в маркетингу
- •2.1. Загальне поняття балансового методу і принципова схема міжгалузевого балансу
- •2.2. Застосування моделі міжпродуктового балансу у маркетингу
- •3. Методи і моделі управління товарними запасами у маркетингу
- •3.1. Класична задача управління запасами
- •3.2. Принципові системи регулювання товарних запасів
- •3.3. Модель економічно вигідних розмірів партій заказу
- •4. Регресійні однофакторні моделі
- •4.1. Лінійне рівняння регресії. Метод найменших квадратів
- •4.2. Нелінійні однофакторні моделі регресії
- •Параболічне рівняння регресії
- •5. Багатофакторні регресійні моделі, їх специфікація та аналіз
- •5.1. Лінійні багатофакторні моделі
- •5.2. Нелінійна багатофакторна модель
- •5.3. Мультиколінеарність факторів
- •6. Моделювання попиту в задачах маркетингу
- •7. Методи експертних оцінок в маркетингових дослідженнях
- •7.1. Основні ідеї методів експертних оцінок
- •7.2. Кореляція рангів та її вимірювання
- •7.3. Випадок двох експертів
- •7.4. Випадок багатьох експертів. Методи визначення середніх рангів
- •8. Комп'ютерна підтримка розрахунків в пакеті excel
- •Література
- •Предметний покажчик
- •Розподіл Фішера при
- •Продовження значень розподілу Фішера при
- •Квантілі розподілу Стьюдента
- •Продовження квантілей розподілу Стьюдента
- •Значення критерію Пірсона
2. Балансові моделі в маркетингу
2.1. Загальне поняття балансового методу і принципова схема міжгалузевого балансу
Статичні і динамічні балансові моделі широко застосовуються для математичного моделювання економічних систем і процесів, у тому числі і у задачах маркетингу. В основі цих моделей лежить балансовий метод, тобто взаємне зіставлення наявних матеріальних, трудових і фінансових ресурсів і потреб у них. Таким чином, під балансовою моделлю розуміють систему рівнянь, які задовольняють вимозі відповідності наявності ресурсу і його використання. При цьому відповідність розуміється або як рівність, або менш жорстко – як достатність ресурсів для задоволення потреби і, отже, наявність деякого резерву.
Необхідно відзначити, що балансові моделі носять, як правило, фактографічний характер і не містять якого-небудь механізму порівняння окремих варіантів економічних рішень, що не дозволяє зробити вибір оптимального розвитку економічної системи. Цим визначається обмеженість балансових моделей і балансового методу в цілому.
Балансові моделі належать до матричних економіко-математичних моделей, у яких балансовий метод дістає строге математичне вираження. Такі моделі поєднує не тільки загальний матричний принцип побудови і єдність системи розрахунків, але і аналогічність економічних характеристик окремих розділів. Це дозволяє розглядати структуру, зміст і основні залежності матричних моделей на прикладі широко поширеної моделі міжгалузевого балансу (МГБ) виробництва і розподілу продукції в народному господарстві. Даний баланс відображає виробництво і розподіл суспільного продукту в галузевому розрізі, міжгалузеві виробничі зв'язки, використання матеріальних і трудових ресурсів, створення і розподіл національного доходу.
Принципова
схема МГБ
виробництва
і розподілу сукупного суспільного
продукту у вартісному
вираженні
наведена
в табл. 2.1. В її покладено
розподіл
сукупного продукту на дві
частини: проміжний і кінцевий продукт.
Все народне господарство
представлене у вигляді сукупності
![]() галузей,
при цьому кожна галузь фігурує в балансі
як виробляюча і як споживаюча. В
схемі МГБ виділяють чотири складові
частини, які мають різний економічний
зміст і називають квадрантами балансу
(вони позначені римськими цифрами).
галузей,
при цьому кожна галузь фігурує в балансі
як виробляюча і як споживаюча. В
схемі МГБ виділяють чотири складові
частини, які мають різний економічний
зміст і називають квадрантами балансу
(вони позначені римськими цифрами).
Перший
квадрант МГБ
– це таблиця міжгалузевих матеріальних
зв'язків,
показники
![]() якої є величинами
прямих міжгалузевих потоків продукції,
де
якої є величинами
прямих міжгалузевих потоків продукції,
де
![]() і
і
![]() – відповідно
номери
виробляючих і споживаючих галузей. Цей
квадрант має вигляд квадратної матриці
розмірності
,
сума
всіх елементів якої дорівнює річному
фонду
відшкодування витрат засобів виробництва
в матеріальній сфері.
– відповідно
номери
виробляючих і споживаючих галузей. Цей
квадрант має вигляд квадратної матриці
розмірності
,
сума
всіх елементів якої дорівнює річному
фонду
відшкодування витрат засобів виробництва
в матеріальній сфері.
Таблиця 2.1 – Принципова схема міжгалузевого балансу
Виробляючі галузі |
Споживаючі галузі |
Кінцевий продукт |
Валовий продукт |
|||
1 |
2 |
… |
|
|||
1 |
|
|
… |
|
|
|
2 |
|
|
… |
|
|
|
… |
… |
… |
І |
… |
ІІ |
… |
|
|
|
… |
|
|
|
Амортизація |
|
|
… |
|
|
|
Оплата праці |
|
|
III |
|
IV |
|
Чистий дохід |
|
|
… |
|
|
|
Валовий продукт |
|
|
… |
|
|
|
У
другому квадранті представлена кінцева
продукція всіх галузей,
що
виходить із сфери виробництва
на споживання і накопичення. Він
характеризує галузеву матеріальну
структуру національного доходу. У табл.
2.1
другий квадрант складає один стовпець
величин
![]() .
В розгорнутій схемі МГБ
кінцевий продукт кожної галузі дається
диференційовано по напрямках
використання: на особисте
і суспільне
споживання, на накопичення, експорт і
т.д.
.
В розгорнутій схемі МГБ
кінцевий продукт кожної галузі дається
диференційовано по напрямках
використання: на особисте
і суспільне
споживання, на накопичення, експорт і
т.д.
Третій
квадрант МГБ
характеризує національний доход з боку
його вартісного складу,
як суму чистої продукції і амортизації.
Чиста продукція розуміється як сума
оплати праці і чистого доходу
галузей. Суму амортизації і чистої
продукції
![]() ї
галузі називають умовно чистою продукцією:
ї
галузі називають умовно чистою продукцією:
![]() .
.
Четвертий квадрант характеризує кінцеве формування і використання національного доходу. Його загальний підсумок, так само як другого і третього квадранту, повинен дорівнювати створеному за рік національному доходу.
Валова продукція галузей не входить у розглянуті вище чотири квадранти, а представлена у вигляді стовпця праворуч від другого квадранта і у вигляді рядка нижче третього квадранта. Рядок і стовпець валової продукції замикають схему МГБ і відіграють важливу роль як для перевірки самого балансу, так і для розробки економіко-математичної моделі МГБ.
З розгляду МГБ випливає, що підсумок матеріальних витрат ї споживаючої галузі і її умовно чистої продукції дорівнює її валовій продукції
![]() ,
(2.1)
,
(2.1)
при
цьому валова продукція
![]() ї
виробляючої галузі дорівнює сумі
матеріальних витрат галузей, що споживають
її продукцію, та її кінцевої продукції
ї
виробляючої галузі дорівнює сумі
матеріальних витрат галузей, що споживають
її продукцію, та її кінцевої продукції
 .
(2.2)
.
(2.2)
Співвідношення (2.1) задають систему рівнянь, що відображають вартісний склад продукції всіх галузей матеріальної сфери. Формула (2.2) описує систему з рівнянь, які називаються рівняннями розподілу продукції галузей матеріального виробництва по напрямках використання.
Системи (2.1) і (2.2) обумовлюють виконання співвідношення
 ,
(2.3)
,
(2.3)
ліва частина якого є сумою третього квадранту, а права – підсумком другого квадранту. Це рівняння показує, що в МГБ дотримується найважливіший принцип єдності матеріального і вартісного складу національного доходу.
Основу інформаційного забезпечення МГБ становить технологічна матриця коефіцієнтів прямих матеріальних витрат на виробництво одиниці продукції. Передбачається, що для виробництва одиниці продукції в й галузі потрібна певна кількість витрат проміжної продукції ї галузі, яка дорівнює
 .
(2.4)
.
(2.4)
Ця
величина
не залежить від обсягу виробництва в
й
галузі і є
досить стабільною величиною
в часі. Величину
![]() називаються
коефіцієнтом
прямих матеріальних витрат.
Він
показує,
яка кількість продукції
ї
галузі є необхідною для виробництва
одиниці продукції
ї
галузі (з
урахуванням
тільки прямих витрат).
називаються
коефіцієнтом
прямих матеріальних витрат.
Він
показує,
яка кількість продукції
ї
галузі є необхідною для виробництва
одиниці продукції
ї
галузі (з
урахуванням
тільки прямих витрат).
З урахуванням (2.4) систему рівнянь балансу (2.2) можна подати як
 .
(2.5)
.
(2.5)
Введемо
матрицю коефіцієнтів прямих матеріальних
витрат
![]() ,
вектор-стовпець
валової продукції
,
вектор-стовпець
валової продукції
![]() і
вектор-стовпець
кінцевої продукції
і
вектор-стовпець
кінцевої продукції
![]()
 ,
,
 ,
,
 .
.
Тоді система рівнянь (2.5) у матричній формі прийме вигляд
![]() .
(2.6)
.
(2.6)
Система рівнянь (2.5), або вона ж у матричній формі (2.6), називається економіко-математичною моделлю міжгалузевого балансу (моделлю В. Леонтьева, моделлю «витрати–випуск»).
З її допомогою можна виконувати три варіанти розрахунків:
Задавши в моделі величини валової продукції кожної галузі
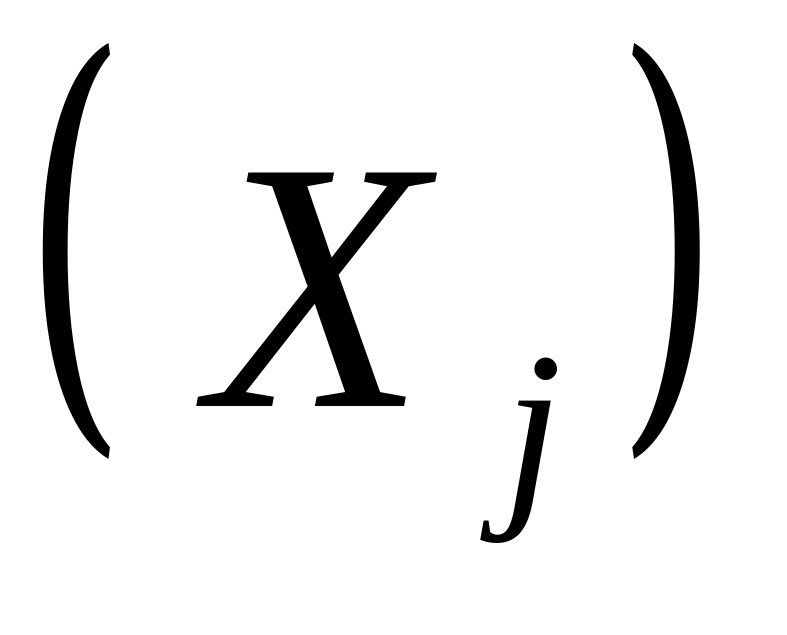 ,
можна
визначити
об’єм
кінцевої продукції кожної галузі
,
можна
визначити
об’єм
кінцевої продукції кожної галузі

![]() .
(2.7)
.
(2.7)
Задавши величини кінцевої продукції всіх галузей , можна визначити величини валової продукції кожної галузі
![]() .
(2.8)
.
(2.8)
Задавши для ряду галузей величини валової продукції, а для всіх інших галузей об’єми кінцевої продукції, можна знайти величини кінцевої продукції перших галузей і обсяги валової продукції інших. У цьому варіанті розрахунку зручніше користуватися не матричною формою моделі (2.6), а скалярною системою лінійних рівнянь (2.5).
У
формулах (2.7) і (2.8) через
![]() позначено
одиничну матрицю
позначено
одиничну матрицю
![]() го
порядку, позначимо
го
порядку, позначимо
![]() .
Тоді
систему (2.8) можна записати у вигляді
.
Тоді
систему (2.8) можна записати у вигляді
![]() .
(2.9)
.
(2.9)
З матричного рівняння (2.9) для будь-якої ї галузі одержимо
 ,
(2.10)
,
(2.10)
де
![]() – елементи матриці
– елементи матриці
![]() .
Вони показують, скільки
потрібно виробити продукції
ї
галузі, щоб з
урахуванням
прямих і непрямих витрат цієї продукції
одержати
одиницю кінцевої продукції
ї
галузі. На відміну від коефіцієнтів
прямих витрат
коефіцієнти
називають
коефіцієнтами
повних матеріальних витрат
і
містять у собі як прямі, так і непрямі
витрати всіх порядків. Якщо прямі витрати
відображають
кількість засобів виробництва, витрачених
безпосередньо при виготовленні даного
продукту, то непрямі відносяться
до попередніх стадій виробництва
і входять у виробництво
продукту не прямо,
а через інші
(проміжні)
засоби
виробництва.
.
Вони показують, скільки
потрібно виробити продукції
ї
галузі, щоб з
урахуванням
прямих і непрямих витрат цієї продукції
одержати
одиницю кінцевої продукції
ї
галузі. На відміну від коефіцієнтів
прямих витрат
коефіцієнти
називають
коефіцієнтами
повних матеріальних витрат
і
містять у собі як прямі, так і непрямі
витрати всіх порядків. Якщо прямі витрати
відображають
кількість засобів виробництва, витрачених
безпосередньо при виготовленні даного
продукту, то непрямі відносяться
до попередніх стадій виробництва
і входять у виробництво
продукту не прямо,
а через інші
(проміжні)
засоби
виробництва.
Отже, валова продукція виступає як зважена сума величин кінцевої продукції, причому вагами є коефіцієнти .
Коефіцієнти повних матеріальних витрат застосовують при визначенні впливу на валовий випуск деякої галузі передбачувана зміна об’ємів кінцевої продукції всіх галузей
 .
(2.11)
.
(2.11)
Тут
![]() і
і
![]() –
зміни
(прирісти)
величин
валової і кінцевої продукції.
–
зміни
(прирісти)
величин
валової і кінцевої продукції.
Зауваження.
Для величин, що складають модель
МГБ,згідно їх змістовному значенню
виконуються умови
![]() ,
,
![]() ,
,
![]()
![]() .
.
Економічна
система забезпечує додатний кінцевий
випуск по всіх галузях, якщо матриця
коефіцієнтів прямих матеріальних витрат
задовольняє умові продуктивності
![]() .
Це
означає існування додатного вектора
кінцевої продукції
.
Це
означає існування додатного вектора
кінцевої продукції
![]() для моделі МГБ
(2.6).
для моделі МГБ
(2.6).
