Параболічне рівняння регресії

Часто залежності між узагальнено-економічними показниками можна описати рівнянням параболи

. (4.15)

Система нормальних рівнянь для визначення параметрів буде мати вигляд

(4.16)

Приклад 4.3. На підставі вибірки з десяти спостережень встановити залежність у вигляді параболічної функції між – товарообігом на 1 працівника (тис.грн.) і – площею торгових залів приміщення на 1 робоче місце (м²).

Розв’язок: Всі розрахунки зведені в допоміжну таблицю 4.6.

таблиця 4.6 – Розрахункова таблиця для приклада 4.3

1	10	1	1	1	100	10	10	6,98	9,12	0,3
2	12	4	8	16	144	24	48	16,45	19,8	0,37
3	28	9	27	81	784	84	252	26,3	2,89	0,06
4	40	16	64	156	1600	160	640	36,53	12,04	0,087
5	42	25	125	625	1764	210	1050	47,14	26,42	0,12
6	52	36	216	1296	2704	312	1872	58,13	37,58	0,12
7	70	49	343	2401	4900	490	3430	69,5	0,25	0,01
8	91	64	512	4096	8281	728	5824	81,25	95,06	0,11
9	95	81	729	6561	9025	855	7695	93,38	2,62	0,02
10	100	100	1000	10000	10000	1000	10000	105,89	34,69	0,06
55	540	385	3025	25333	39302	3873	30821		240,48	1,25

В останньому рядку записані суми по стовпцях.

Система рівнянь (4.16) має вигляд

В результаті її розв’язання одержимо: . Отже, рівняння регресії згідно відношенню (4.15) має вигляд

. (4.17)

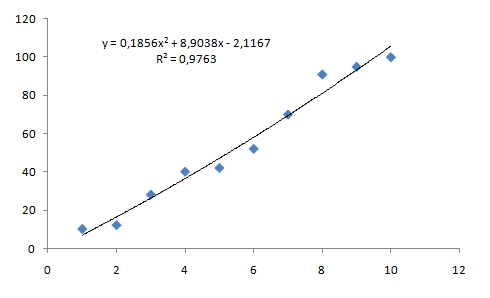
Рисунок 4.2 – Графік і рівняння параболічної залежності

Оцінка точності рівняння параболи (4.17) становить і вказує на дуже високу ступінь адекватності знайденого рівняння регресії.

Середнє квадратичне залишкове відхилення для рівняння регресії (4.17) дорівнює (тут , бо модель (4.15) залежить від

трьох параметрів , , ).

Дисперсія показника дорівнює . Кореляційне відношення вказує на дуже тісний кореляційний зв'язок між показниками та .

Адекватність моделі перевіряємо за допомогою критерію Фішера (4.9):

; . Маємо , отже, модель адекватно описує залежність між товарообігом на одного працівника та площею торгових залів приміщення на одне робоче місце.

Експоненціальне рівняння регресії

Для моделювання деяких економічних явищ чи процесів в якості функції регресії застосовують експоненціальну залежність

, (4.18)

яка визначається двома параметрами і .

Щоб застосувати метод найменших квадратів до підбору коефіцієнтів, в цьому випадку потрібно зробити наступні попередні перетворення: прологарифмувати рівність (4.18), ввести нову змінну , тоді одержане рівняння

(4.19)

буде рівнянням прямої, для якого невідомі параметри і обчислюють за відомими формулами МНК.

Співвідношення (4.19) є лінеаризированим рівнянням експоненти. До нього застосовують метод найменших квадратів. Система нормальних рівнянь при цьому має вигляд або

(4.20)

Приклад 4.4. Проведено сім спостережень за економічними показниками: – об’єм продажу меблів на душу населення по Донецькій області і – товарообіг на 1 робітника (тис. грн.). За даними вибірки (табл. 4.7) скласти рівняння регресії в формі експоненти (4.18).

Таблиця 4.7 – Дані приклада 4.4

Товарообіг на 1 робітника	20	70	120	170	220	270	320
Об’єм продажу меблів на душу населення	17,8	21,6	23,9	24,8	27,2	29,2	30,2

Розв’язок: Усі допоміжні розрахунки зведено в таблицю 4.8.

Таблиця 4.8 – Допоміжна розрахункова таблиця

20	17,8	2,88	400	57,6	18,99	-1,19	1,42	6,69
70	21,6	3,07	4900	214,9	20,68	0,92	0,85	4,26
120	23,9	3,17	14400	380,4	22,52	1,38	1,90	5,77
170	24,8	3,21	28900	545,7	24,51	0,29	0,08	1,17
220	27,2	3,30	48400	726	26,69	0,51	0,26	1,88
270	29,2	3,37	72900	909,9	29,06	0,14	0,02	0,48
320	30,2	3,41	102400	1091,2	31,63	-1,43	2,05	4,74
	174,2	22,41	272300	3925,7			6,58	24,99

З системи (4.21) визначаємо значення параметрів і . Отже, регресійне рівняння має вигляд або

. (4.21)

Деяка розбіжність оцінок параметрів регресійного рівняння пояснюється розрахунковою погрішністю проведених обчислень (див. рис. 4.3).

Оцінка точності одержаного експоненціального рівняння регресії вказує на задовільну адекватність моделі.

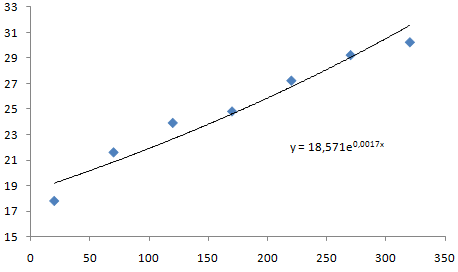
Рисунок 4.3 – Побудова експоненціальної залежності

Залишкове среднєквадратичне відхилення 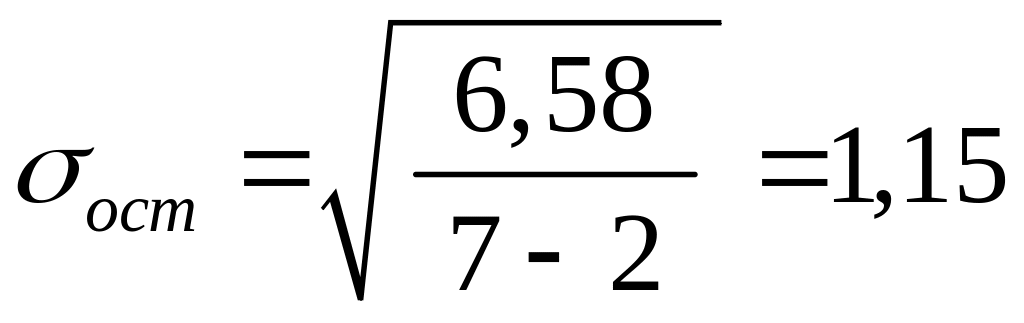і дисперсія вибірки обумовлюють спостережене значення критерію Фішера . За таблицями критичних точок розподілу Фішера знаходимо критичне значення . Тут виконується умова , тому одержане рівняння експоненти адекватно описує економічний процес.