Упражнения

1. Вычислите:

1. i⁶⁶; i¹⁴³; i²¹⁶; i¹³⁷.

2. i⁴³+i⁴⁸+i⁴⁴+i⁴⁵.

3. (i³⁶+i¹⁷)i²³.

4. (i¹³³+i¹¹⁵+i²⁰⁰+i¹⁴²)(i¹⁷+i³⁶).

5. i¹⁴⁵+i¹⁴⁷+i²⁶⁴+i³⁴⁵+i¹¹⁷.

6. (i¹³+i¹⁴+i¹⁵)i³².

7. (i⁶⁴+i¹⁷+i¹³+i⁸²)(i⁷²-i³⁴).

2. Найдите действительные значения x и y из равенств:

1. 7x+5i=1-10iy.

2. (2x+y)-i=5+(y-x)i.

3. x+(3x-y)i=2-i.

4. (1+2i)x+(3-5i)y=1-3i.

5. (2-i)x+(1+i)y=5-i.

6. (3i-1)x+(2-3i)y=2-3i.

3. Произведите сложение и вычитание комплексных чисел:

1. (3+5i)+(7-2i).

2. (6+2i)+(5+3i).

3. (-2+3i)-(7-2i).

4. (5-4i)+(6+2i).

5. (3-2i)-(5+i).

6. (4+2i)-(-3+2i).

7. (-5+2i)+(5+2i).

8. (-3-5i)+(7-2i).

4. Произведите умножение комплексных чисел:

1. (2+3i)(5-7i).

2. (6+4i)(5+2i).

3. (3-2i)(7-i).

4. (-2+3i)(3+5i).

5. (1–i)(1+i).

6. (3+2i)(1+i).

7. (6+4i)·3i.

8. (2-3i)(-5i).

5. Выполните действия:

1. (3+5i)².

2. (2-7i)².

3. (3+2i)³.

4. (3-2i)³.

5. (3+2i)(3- 2i).

6. (5+i)(5-i).

7. (a+bi)(a-bi).

6. Выполните действия:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

7. Решите уравнения:

1. x²–4x+13=0;

2. x²+3x+4=0;

3. 2,5x²+x+1=0;

4. 4x²–20x+26=0.

8. Изобразите на комплексной плоскости области, удовлетворяющие следующим неравенствам:

1. |z-i|<3;

2. ;

3. Rez<1;

4. .

9. Запишите в тригонометрической и показательной форме комплексные числа:

1. ;

2. ;

3. ;

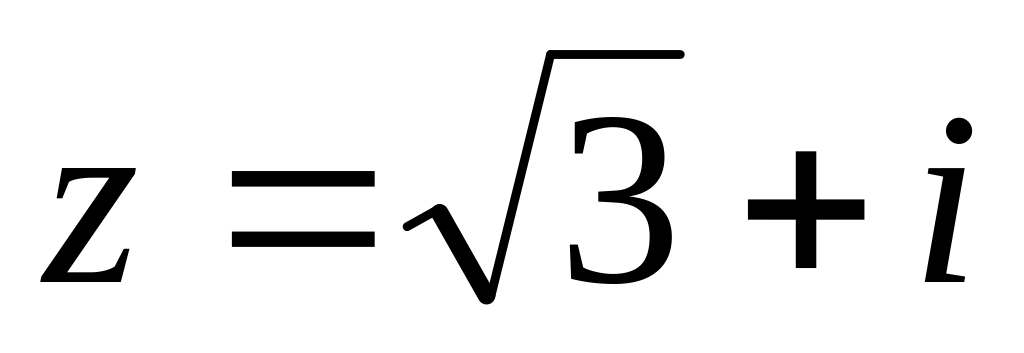4. z=5;

5. z=-10;

6. z=6i.

10. Вычислите:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. :

9. .

Глава 2. Системы линейных уравнений

Линейные уравнения и системы вида (1) с действительными коэффициентами решаются в средней школе. Наша цель – научиться оперировать с системой линейных алгебраических уравнений самого общего вида:

(2)

Будучи, казалось бы, чисто количественным, усложнение, получающееся при переходе от (1) к (2), имеет на самом деле принципиальное значение. Системы вида (2) встречаются буквально во всей математике и так называемые линейные методы, конечным продуктом которых часто являются решения линейных систем, составляют ее наиболее развитую часть. Достаточно упомянуть, что теория систем вида (2) послужила в конце XIX века прототипом для создания теории интегральных уравнений, играющих исключительно важную роль в механике и физике. Решение большого числа практических задач на компьютерах также сводится к системам (2).

2.1. Общие сведения о системах линейных уравнений

Вспомним решение одного линейного уравнения и системы из двух линейных уравнений с двумя неизвестными:

I.

1. Если , - единственное решение,

2. Если ,

   1. - бесконечное множество решений,

   2. - решений нет.

II.

1. - единственное решение (графически: прямые пересекаются),

2. - бесконечное множество решений (прямые совпадают),

3. -  (решений нет) (прямые параллельны).

Определение. Система выражений вида

(2.1)

где - коэффициенты при неизвестных, причем , , - неизвестные, - свободные члены, называется системой линейных уравнений, состоящей из m уравнений с n неизвестными.

Определение. Коэффициенты при неизвестных системы (2.1) образуют прямоугольную таблицу чисел, которую будем называть матрицей данной системы:

- основная матрица,

- расширенная матрица.

Определение. Решением системы (2.1) называется упорядоченная последовательность чисел , если при подстановке чисел в систему (2.1) вместо неизвестных соответственно каждое из уравнений системы (2.1) обращается в верное равенство (тождество).

Определение. Если то систему (2.1) будем называть однородной системой линейных уравнений. Если то систему (2.1) будем называть неоднородной системой линейных уравнений.

Определение. Систему линейных уравнений будем называть совместной, если она имеет хотя бы одно решение. Если система (2.1) не имеет решений, то будем ее называть несовместной.

Определение. Совместную систему будем называть определенной, если она имеет одно решение. Если совместная система имеет более одного решения, будем называть неопределенной.

Рассмотрим систему линейных уравнений, состоящую из m уравнений с n неизвестными:

Определение. Система линейных уравнений называется следствием системы (2.1), если каждое решение системы (2.1) является решением системы .

Определение. Если обе системы (2.1) и являются следствием друг друга, то они называются равносильными.

Под этим понимают, что они имеют одно и то же множество решений (возможно, пустое).

Теорема. Любая подсистема данной системы линейных уравнений является следствием данной системы.