Лабораторная работа № 2

ГЕНЕРИРОВАНИЕ ПОЛУБЕСКОНЕЧНЫХ

ПСЕВДОСЛУЧАЙНЫХ ПРОЦЕССОВ

Цель работы: построение нерекурсивных и рекурсивных генераторов полубесконечных процессов с заданными корреляционными свойствами.

1. Интегральное уравнение генератора полубесконечного процесса

Базовая модель шума в радиоэлектронике и других приложениях: шум – стационарный процесс , - функция корреляции. Процесс считается полубесконечным, если его протяженность , - интервал корреляции. На практике генерируется одна достаточно протяженная реализация шума. Задача генерирования шума формулируется как задача окрашивания белого шума: надо синтезировать линейный фильтр, преобразующий белый шум в окрашенный – имеющий заданную функцию корреляции .

Линейный фильтр описывается сверткой: сигнал на его выходе [1]

, (1)

- сигнал на входе, - весовая функция фильтра. Если , то среднее значение , а функция корреляции сигнала (1)

. (2)

Функция (2) записана в самом общем виде - как функция корреляции нестационарного процесса, например, для выходного сигнала в неустановившемся режиме.

Если - белый шум (с функцией корреляции ), то интеграл

по фильтрующему свойству - функции записывается

.

В установившемся режиме - стационарный процесс, его функция корреляции – функция разности аргументов, то есть

.

Обычно последнее соотношение записывают с дисперсией :

, (3)

так как безразлично, как обозначать переменные интегрирования.

Если функция задана, то соотношение (3) становится интегральным уравнением относительно неизвестной весовой функции . Решить уравнение (3) – значит решить задачу синтеза линейного фильтра, окрашивающего белый шум. Другими словами, интегральное уравнение (3) можно назвать уравнением генератора стационарного гауссова процесса с заданной функцией корреляции.

Общее решение уравнения (3) приведено в [2]:

, (4)

- число сочетаний из по , повторные функции

,

, .

Для типовых функций корреляции [2]

1) ,

2) ,

3) ,

4) ,

5) ,

решения уравнения

1) ,

2) ,

3) ,

4) ,

5) .

На рис. 1 приведен пример функций и для четвертого варианта при , .

Рис. 1. Функция корреляции и весовая функция

2. Интервал дискретизации

Реализация генератора на ЦВМ требует перехода от непрерывных функций (5) и (6) к дискретным – векторам и . На входе и выходе генератора также дискретные сигналы – последовательности (векторы) случайных чисел и . Значения вектора формируются по правилу дискретной свертки [1] – дискретного аналога свертки (1)

, , (7)

- длина формируемого вектора.

При построении любой дискретной системы принципиальным является назначение интервала дискретизации , с которым берутся отсчеты непрерывных сигналов и функций. По теореме Котельникова интервал дискретизации

, (8)

где - верхняя граничная частота полосы частот системы. Знак равенства в (8) справедлив для сигналов бесконечной длительности. Так как реальный вектор , хотя и протяженной, но конечной длительности, значение может быть уменьшено. Реальный смысл выбора интервала дискретизации понятен: он должен быть достаточно большим, чтобы количество отсчетов было минимальным, и достаточно малым, чтобы хорошо отслеживались особенности дискретизируемых сигналов и функций. Базовым значением можно назначить и далее его уточнить экспериментально.

Спектр мощности стационарного процесса с функцией корреляции находится ее Фурье – преобразованием. Функция корреляции симметрична, поэтому Фурье – преобразование записывается как косинус – преобразование:

.

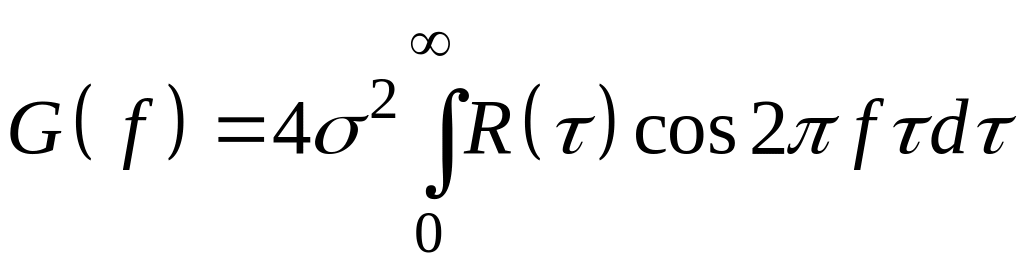Для функций корреляции (5) спектры мощности равны соответственно

1) ,

2) ,

3) ,

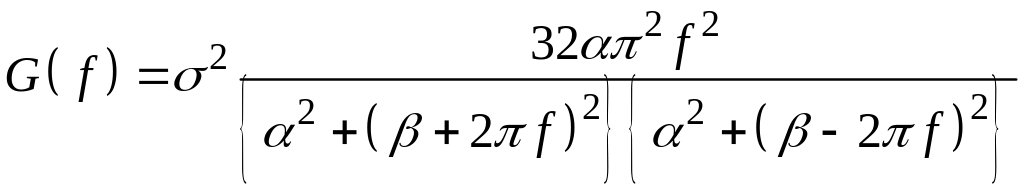4) ,

5) .

Мощность случайного процесса при . Верхняя граничная частота находится из условия , , например, как , при которой .

Пример 1. Расчет спектра мощности процесса с функцией корреляции и интервала дискретизации по теореме Котельникова. Спектр мощности

.

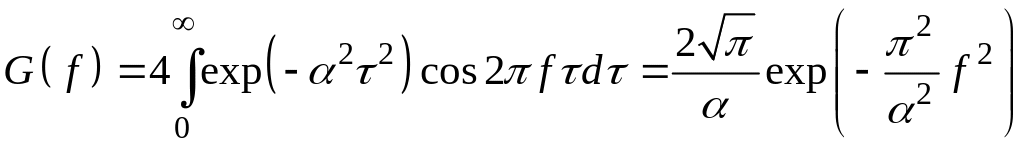Функции , показаны на рис. 2 для значений параметра и . Расчет вероятности может выполняться в SIGNAL PROCESSING функцией TRAPZ(f,G), в SYMBOLIC MATH - функцией INT(G,0,F) [3]. Например, значение достигается при для и при для . Следовательно, интервал дискретизации можно назначить равным в первом случае и во втором.

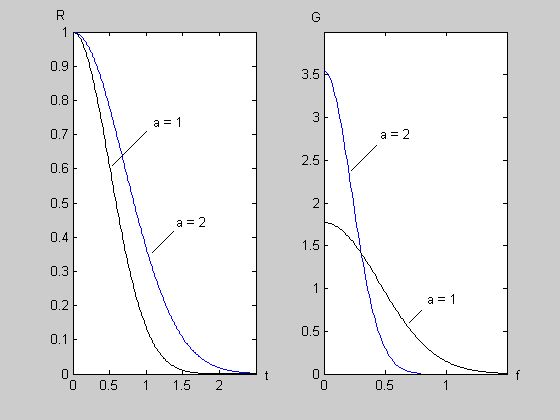
Рис. 2. Функция корреляции, спектр мощности

Можно также воспользоваться функцией CUMSUM (накапливающееся суммирование) в SIGNAL PROCESSING (рис. 3):

clear

T=1.5

del=0.01

f=0:del:T;

a=1

g=2*sqrt(pi)/a*exp(-pi^2/a^2*f.^2)

a1=2

g1=2*sqrt(pi)/a1*exp(-pi^2/a1^2*f.^2)

p=cumsum(g)*del; % интегрирование по формуле прямоугольников

p1=cumsum(g1)*del;

p=p/max(p); % нормировка к единице

p1=p1/max(p1);

plot(f,p,’r’,f,p1)

Нормировка необходима потому, что интегрирование по формуле прямоугольников выполняется с погрешностями. Верхняя граничная частота назначается приблизительно по признаку достижения мощностью значения единица. Конечно, визуальный метод менее точен.

Рис. 3. Зависимость мощности от полосы частот