2.10. Фундаментальная система решений однородной системы линейных уравнений

Определение. Фундаментальной системой решений однородной системы линейных уравнений (ФСР ОСЛУ) называется система решений, которая удовлетворяет следующим условиям:

1. является линейно независимой;

2. каждое решение данной системы линейных уравнений линейно выражается через эту систему решений.

Теорема. ФСР ОСЛУ содержит n-r решений, где n - число неизвестных, r – ранг основной матрицы системы.

Прежде чем доказать теорему, рассмотрим следующий пример.

Пример.

Найти ФСР ОСЛУ:

ФСР состоит из n-r= 5-3=2 векторов.

Пусть - главные неизвестные, - свободные неизвестные.

Общее решение системы .

По-другому: .

.

Доказательство теоремы

Рассмотрим систему линейных уравнений

(2.6)

I. Обозначим - ранг матрицы; n – число неизвестных.

Пусть первые r строк и первые r столбцов линейно независимы.

- неособенная и может быть приведена к единичной с помощью элементарных строчечных преобразований.

Однородная система линейных уравнений, соответствующая матрице С

(2.6')

равносильна исходной системе линейных уравнений.

Пусть - главные неизвестные; - свободные неизвестные.

II. Придавая свободным неизвестным произвольные значения, вычислим соответствующие значения главных неизвестных.

В частности,

, ,…,

(2.7).

Покажем, что система (2.7) является фундаментальной системой решений однородной системы линейных уравнений системы (2), а следовательно и исходной системы.

III. Покажем, что система (2.7) является линейно независимой.

Рассмотрим равенство:

(2.8)

Выполнив в левой части этого равенства операции умножения на скаляр и сложения векторов, получим:

Из этого равенства видно, что по

Равенство (2.8) выполняется при нулевом наборе скаляров, следовательно (2.7) – линейно независима.

IV. Покажем, что каждое решение ОСЛУ линейно выражается через систему (2.7).

Пусть - какое-либо решение системы (2.6). Тогда

=

= = из системы (2.6') получаем =

=

,

Так как получили, что любое решение системы линейных уравнений линейно выражается через систему (2.7), доказательство теоремы завершено.

Упражнения

11. Решить системы уравнений методом Гаусса

1. ;

2. ;

3. ;

4. ;

5. .

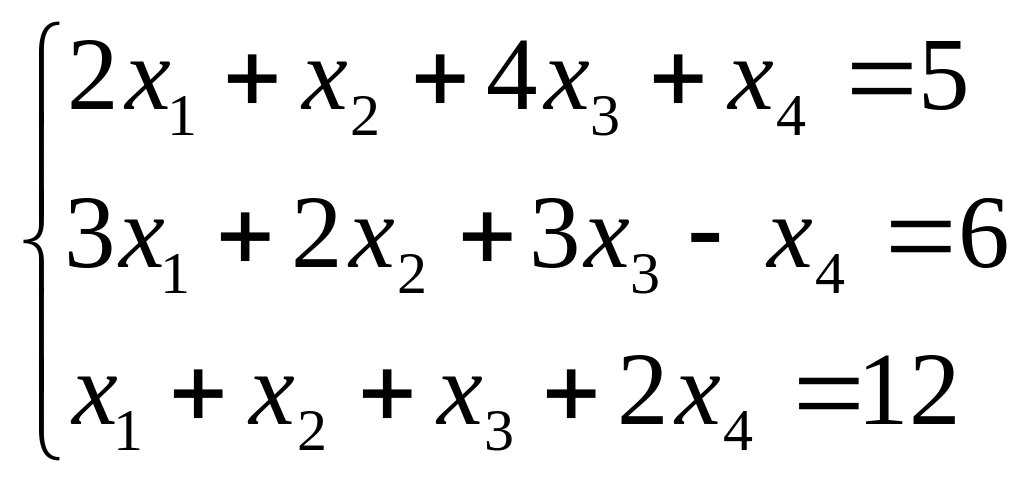12. Исследовать методом Гаусса системы с параметром

1. ;

2. ;

3. ;

4. .

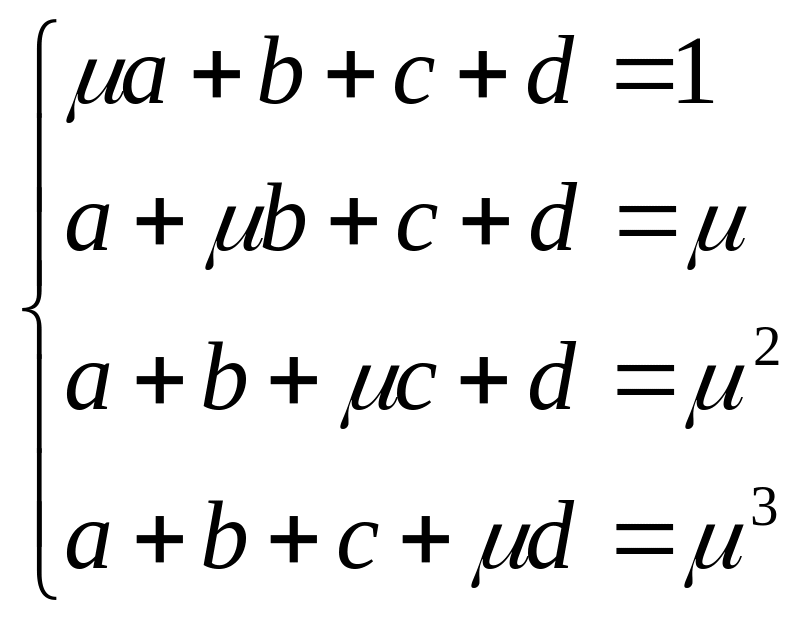13. При каких значениях параметра m система имеет единственное решение?

14. Найти общее решение и ФСР ОСЛУ

1. ;

2. ;

3. .

15. Подобрать параметр так, чтобы система уравнений имела решение

1. ;

2. ;

3. .

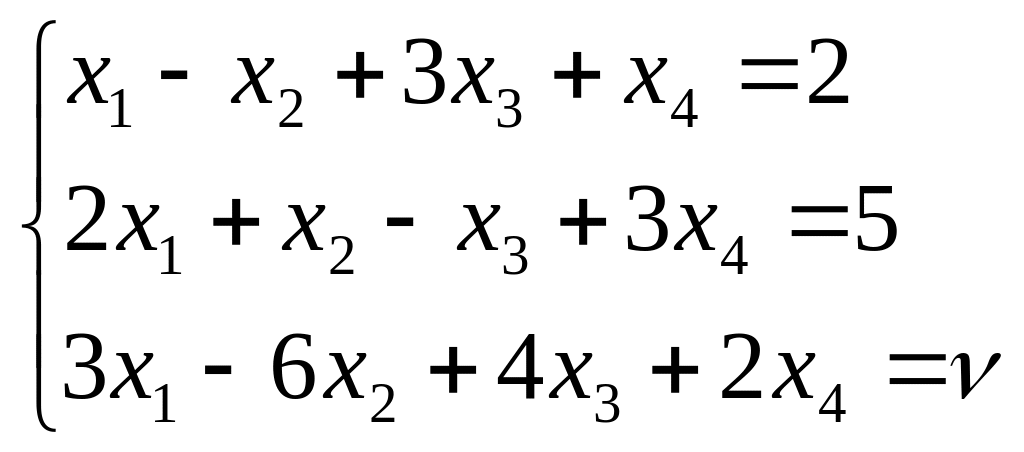16. Дана конечная система векторов:

Найти

1. ;

2. ;

3. .

17. Дана система векторов: _{, ,} Найти:

1. ;

2. ;

3. .

18. Является ли линейно зависимой следующая система векторов?

1. , , ;

2. , ;

3. , , , .

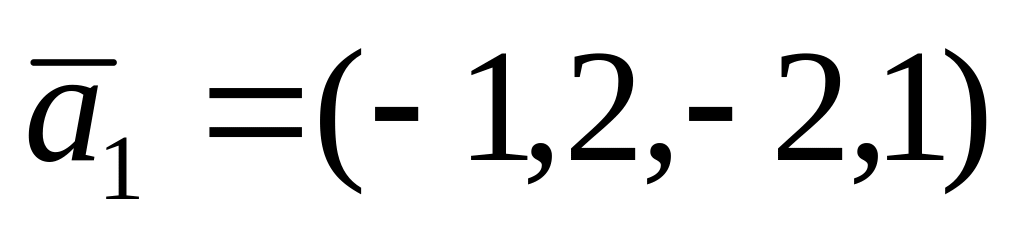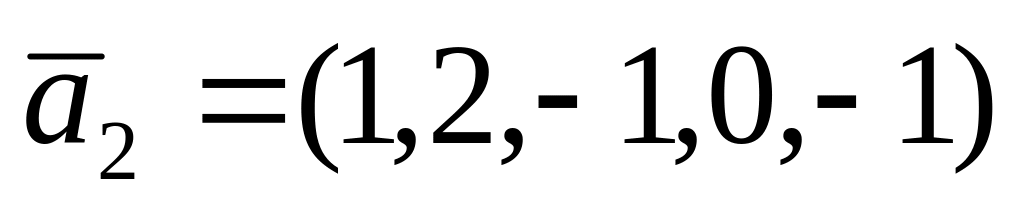19. Показать, что данная система векторов является линейно независимой:

1. , , ;

2. , , ;

3. , , .

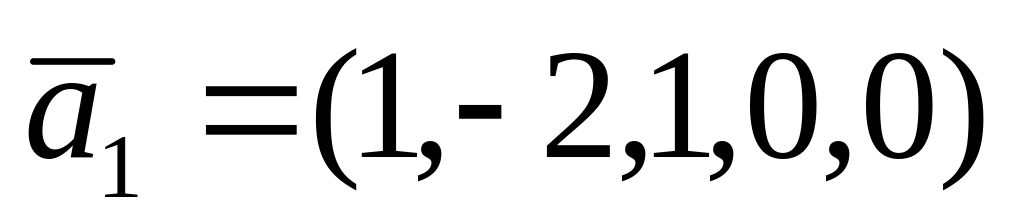20. Выяснить, является ли следующая система векторов линейно зависимой. Найти ее базис и ранг.

1. , , , , ;

2. ;

3. , , , .

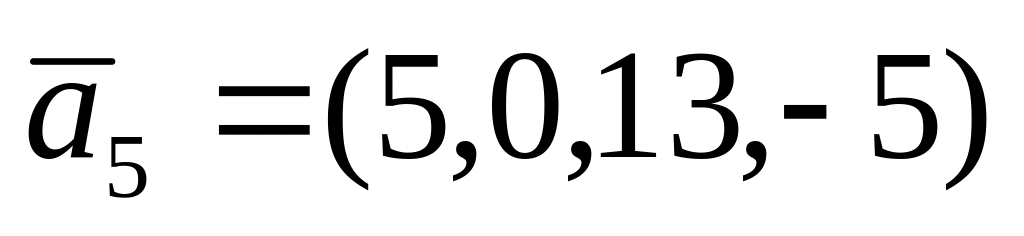21. Доказать, что если можно единственным образом выразить как линейную комбинацию 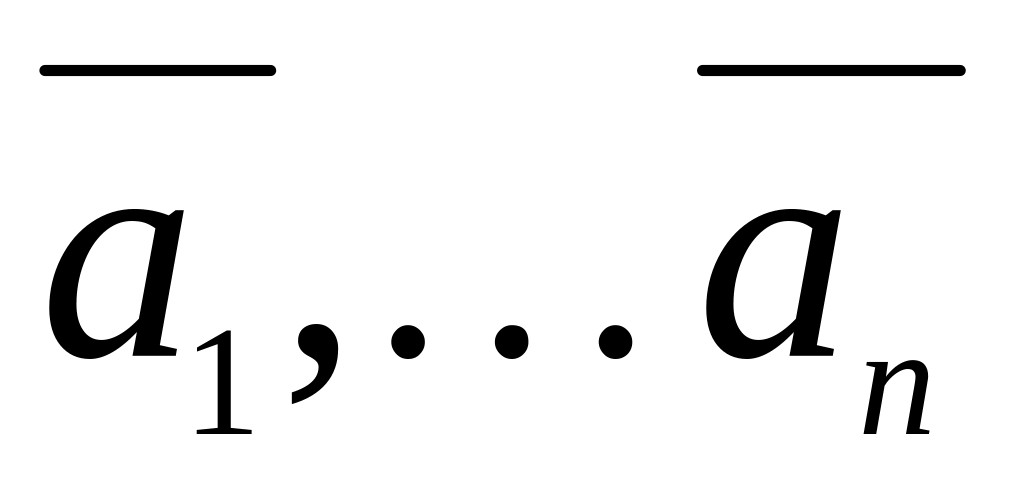, то - линейно независимая система.

22. Найти ранги матриц:

1. ;

2. ;

3. ;

4. .